令M1=m为行星质量,M2=M为太阳质量,分别以行星与太阳为研究对象,应用式(3-6)和式(3-7),则可以得到如下方程:
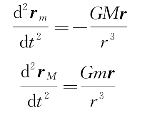
其中,rm与rM分别为行星与太阳在给定惯性坐标系下的位移矢量,上两式相减,就得到太阳-行星向径r(r=rm-rM)的二阶微分方程

这就是行星的运动方程。它的解有6个独立的积分常数,可以取为6个轨道根数。因此,行星轨道运动便完全由6个轨道根数决定。
行星的运动方程(3-8)的积分结果表明,行星运动轨道在一个平面上,轨道是圆锥曲线。
圆锥曲线的一种较普遍形式是椭圆,用平面解析几何的极坐标方程表示为

式中,a是轨道半长径,e是轨道偏心率,θ是近点角(从近日点算起的极角)。于是,行星的6个轨道根数(见图3-10)如下:
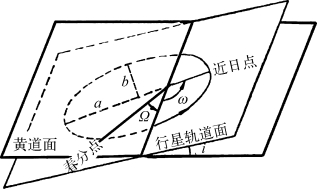
图3-10 行星轨道根数
(1)轨道半长径a,即椭圆的半长轴(a>0),它表示轨道的大小,常称为行星到太阳的平均距离。
(2)轨道偏心率e,即焦点到椭圆中心的距离(a2-b2)1/2(b是半短轴)与半长径a之比,0<e<1,它表示轨道形状。若e=0,则是正圆。
(3)轨道(面)倾角i,常取行星轨道面对黄道面的夹角。i<90°表示行星与地球的轨道运动同向。有些小行星和彗星的轨道运动方向与地球的轨道运动相反,180°>i>90°。
(4)升交点黄经Ω,行星轨道面与黄道面的交线称为交点线,行星从南到北运动经过交点线的点称为升交点,太阳-春分点方向与太阳-行星轨道升交点方向的夹角称为升交点黄经。轨道倾角i和升交点黄经Ω确定行星轨道面的空间位置。(https://www.xing528.com)
(5)近日点角距ω,这是太阳-(行星)近日点方向与太阳-(行星)升交点方向的夹角,它确定行星轨道椭圆长轴的方位。一般常用近日点黄经代替近日点角距。
(6)过近日点时刻τ,可取行星任何一次过近日点的时刻,由它往前后计算行星的位置。
除了椭圆,从行星的运动方程还可得到另两种圆锥曲线(见图3-11):抛物线(a=∞,e=1)和双曲线(a<0,e>1),其特性如表3-1所示。常用近日距代替轨道半长径作为它们的轨道根数。此外,还常用另一些量表示轨道特征,但它们可以由上述6个轨道根数计算出来,例如:
![]()
表3-1 三种轨道的特性
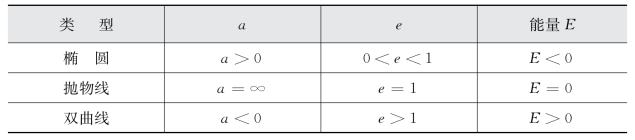
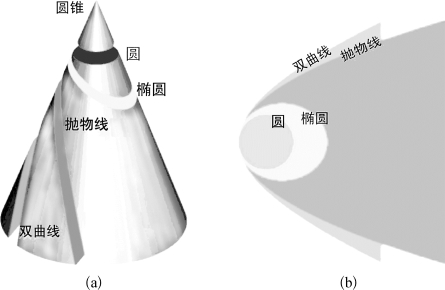
图3-11 圆锥的截面与相应的三种轨道
(a)圆锥的截面;(b)三种轨道
由运动方程得出修正的开普勒第三定律:

考虑到m≪M,则开普勒第三定律就是它的近似。
修正的开普勒第三定律常用于计算天体的质量。当m≪M时,例如,行星的质量远小于太阳质量,则由式(3-11)可得出:

免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




