开普勒定律和万有引力定律的解析

1）开普勒定律

第谷·布拉赫（Tycho Brahe）做了大量的行星位置准确观测，开普勒用这些资料来改进哥白尼日心体系理论。他用哥白尼的匀速圆轨道算出的火星位置与观测偏差8′。“就凭这8′的差异，引起了天文学的全部革命。”经过大量计算分析，他在1609年发现火星轨道不是正圆，而是椭圆（见图3-9），且运动不是匀速的。他把一系列研究结果总结成行星运动三大定律：

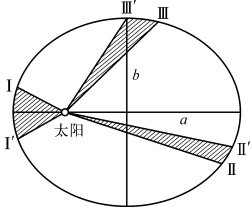
图3-9　行星轨道椭圆和面积定律

（1）行星绕太阳运动的轨道是椭圆，太阳位于椭圆的一个焦点上（椭圆定律）；

（2）连接太阳到行星的直线（向径r）在相等的时间扫过的面积相等（面积定律）；

（3）行星公转周期P的平方与轨道半长径a的立方成正比，即对下标i=1，2，3，…表示的各行星有

式中，K为常数。当公转周期P以恒星年为单位，半长径a用天文单位时，

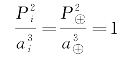(www.xing528.com)

由此可见，由测定行星公转的周期，用式（3-5）就可得出行星公转轨道的半长径。

2）万有引力定律

1687年，牛顿发表名著《自然哲学的数学原理》，提出物体运动的三定律：

（1）无外力作用于物体时，它保持静止或匀速直线运动状态（惯性定律）；

（2）物体受外力F作用，就在外力方向得到加速度a，加速度的大小与外力成正比、与物体的质量m成反比，即

（3）第一个物体受到第二个物体的作用力，同时第一个物体对第二个物体有反作用力，作用力与反作用力总是大小相等、方向相反。

牛顿从这三定律和开普勒定律出发，用微积分理论推演出万有引力定律：两个物体之间的引力大小F与它们质量（M1和M2）的乘积成正比，与它们距离（r）的平方成反比，即

式中，G=6.672×10-8dyn^[1]·cm2／g2=6.672×10-11N·m2／kg2为引力常数。