球面的基本概念和性质-天文学教程上册

1）球面上的圆和它的极

通过球心的平面与球面交线的圆最大而称为大圆，其半径就是球半径，大圆把球面分为相等和对称的两部分。不经过球心的平面与球面交线的圆都较小而称为小圆。球面三角学一般只涉及大圆，前述的天球基本圈（天赤道、地平圈、天子午圈、天卯酉圈）都是大圆。

经过球面上的一个圆（无论大圆还是小圆）所在平面的圆心，作垂直于该平面的球直径，它的两个端点称为该圆的极。例如，图2-3球面上的小圆ABC，经过其所在平面ABC的圆心O′的球直径POP′的两个端点P和P′就是该小圆的极。天顶和天底就是地平圈的极，北、南天极是天赤道的极，东点E和西点W是天子午圈的极，北点N和南点S是天卯酉圈的极。所在平面相互平行的各圆应有共同的极，且只有经过球心的一个圆是大圆。

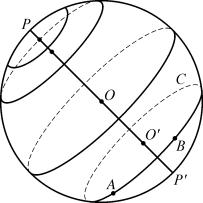
图2-3　球面上的圆和极

2）球面上两点间的角距

在球面三角学中，球面上两点A与B间的距离用连接A与B的大圆弧（较短段）角距表示，即用此两点在球心O的张角∠AOB表述（见图2-4）。

在天文学中，角和圆弧段有三种量度单位：角度（°）、角分（′）、角秒（″）；小时（h）、时分（m）、时秒（s）；弧度（rad）。弧度与角度之间的基本换算关系为

角度（°）、角分（′）、角秒（″）与小时（h）、时分（m）、时秒（s）的换算关系为(www.xing528.com)

对于很小角θ″，可以取

3）球面角

两个大圆弧相交所成的角称为球面角，其交点称为球面角的顶点，大圆弧段称为球面角的边。图2-5中，大圆弧段（两边）PA与PB交于顶点P，构成球面角APB。球面角以过顶点P所作两边（大圆弧）的切线（PC与PD）夹角∠CPD来度量，它等于两边（大圆弧）所在平面所夹的二面角；作P为极的大圆QQ′，两边所在平面交于大圆QQ′的A′和B′点，则∠A′OB′就是该二面角。

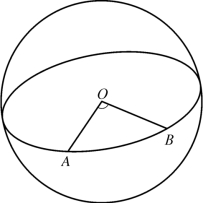
图2-4　球面上两点的角距

图2-5　球面角