多桩矩形承台受弯计算及破坏特征分析

（一）受弯计算

柱下多桩矩形承台在配筋不足情况下将产生弯曲破坏，其破坏特征呈梁式破坏。所谓梁式破坏，指挠曲裂缝在平行于柱边两个方向交替出现，承台在两个方向交替呈梁式承担荷载（图9.1.3），最大弯矩产生在平行于柱边两个方向的屈服线处。利用极限平衡原理可导得两个方向的承台正截面弯矩计算公式。

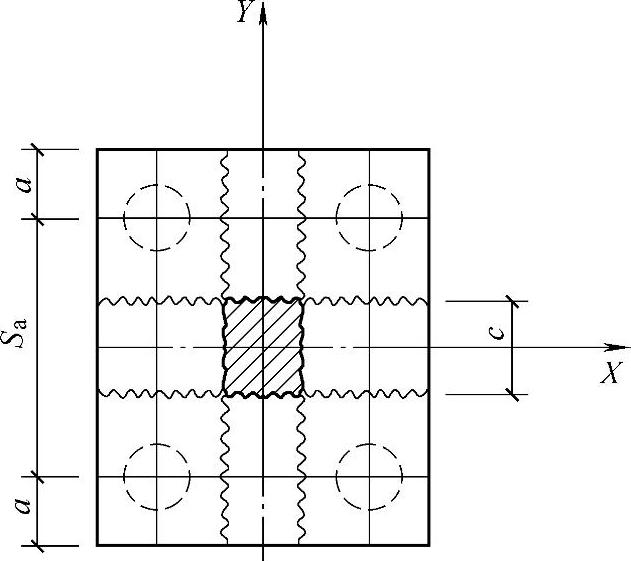
图9.1.3 四桩承台破坏模式

1.弯矩设计值

《建筑桩基技术规范》5.9.2条讲述该项内容，具体如下：

5.9.2 柱下独立桩基承台的正截面弯矩设计值可按下列规定计算：

1 两桩条形承台和多桩矩形承台弯矩计算截面取在柱边和承台变阶处（见图5.9.2a），可按下列公式计算：

式中 M_x、M_y——绕X轴和绕Y轴方向计算截面处的弯矩设计值；

x_i、y_i——垂直Y轴和X轴方向自桩轴线到相应计算截面的距离；

N_i——不计承台及其上土重，在荷载效应基本组合下的第i基桩或复合基桩竖向反力设计值。

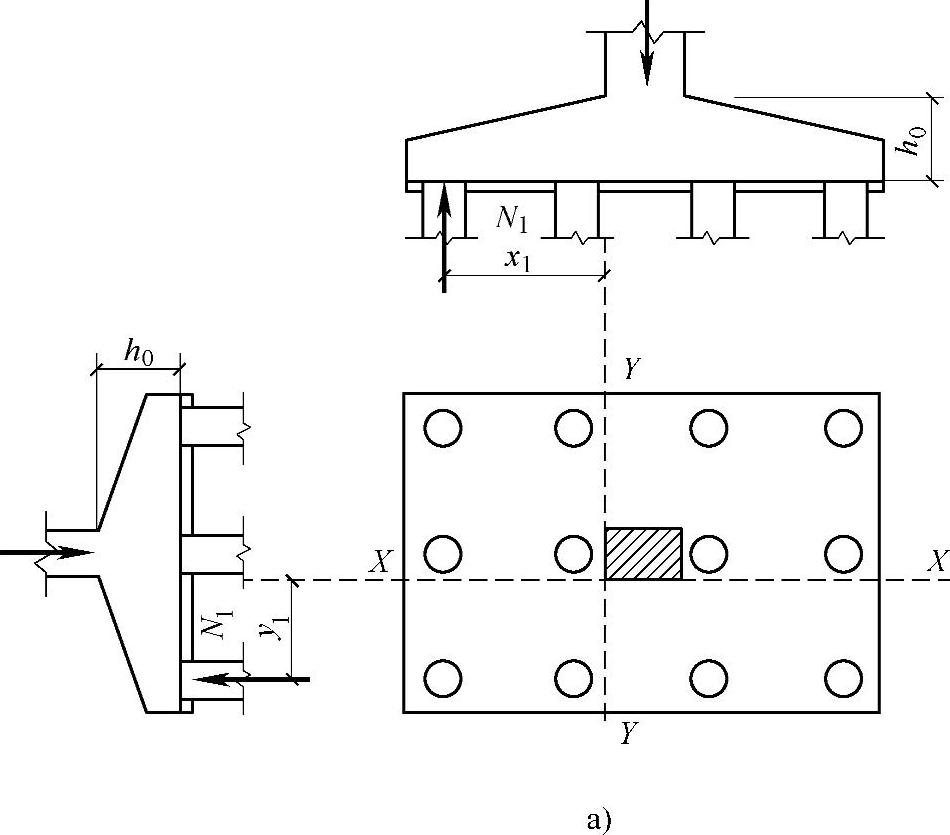
图5.9.2 承台弯矩计算示意

a）矩形多桩承台

【9.1.3】 （2000年二级考题）

四桩独立柱基础如图9.1.4所示，已知每根桩（不计承台及其上土重）在荷载效应基本组合下的基桩竖向反力）设计值均为200kN，试指出承台最大弯矩设计值M_max应为下列何项数值？

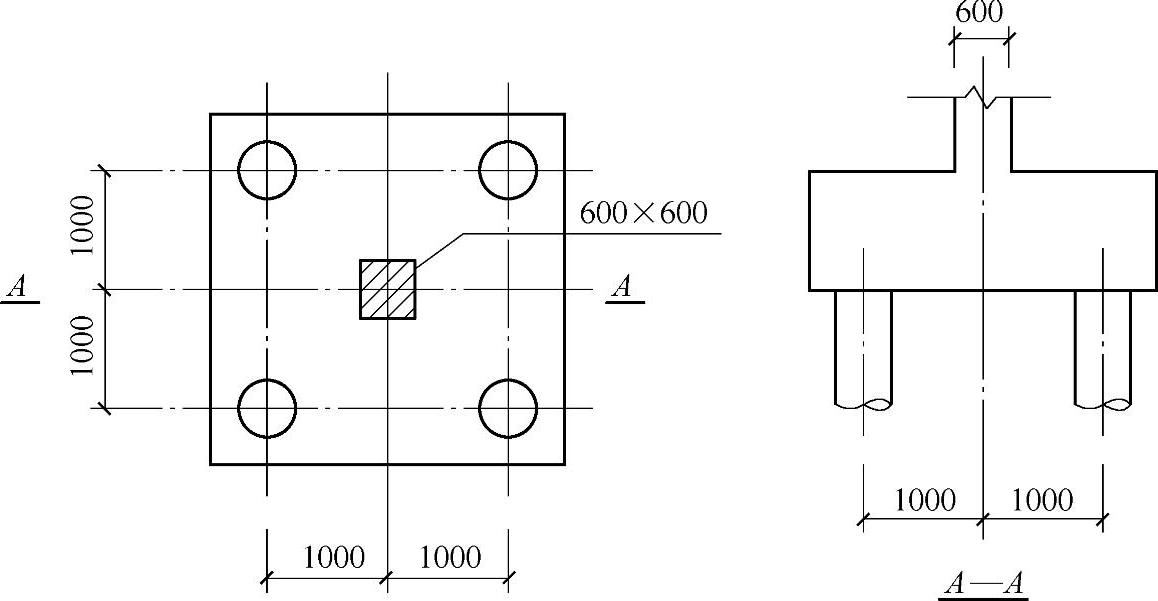
图 9.1.4

（A）400kN·m （B）200kN·m （C）280kN·m （D）140kN·m

【答案】 （C）

【详解】 做题提示：规范5.9.2条中的N为不计承台及其上土重、在荷载效应基本组合下的基桩竖向反力设计值，即取承台顶面处的竖向力设计值来计算基桩竖向反力。

根据《建筑桩基技术规范》式（5.9.2⁃2），承台的最大弯矩设计值为

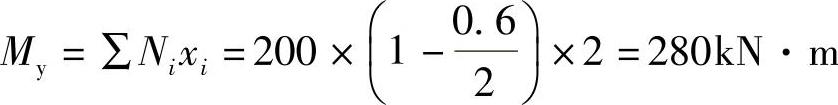
故（C）正确。

【简解】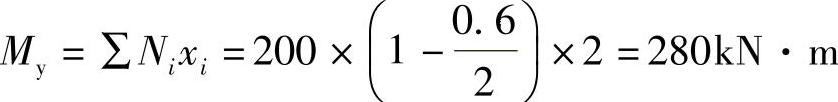

【9.1.4】 （2008年岩土考题）

作用于桩基承台顶面的基本组合下的竖向力设计值为5000kN，x方向的偏心距为0.1m，不计承台及承台上土自重，承台下布置4根桩，如图9.1.5所示。根据《建筑桩基技术规范》计算，承台承受的正截面最大弯矩（kN·m）与下列哪个选项的数值最为接近？

（A）1999.8 （B）2166.4 （C）2999.8 （D）3179.8

【答案】 （B）

【解答】 做题提示：公式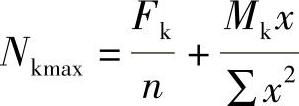和M_max=∑N_maxx_i中的x的取值不同，前者为自桩轴线到y轴线的距离；后者为自桩轴线到计算截面的距离。

根据《建筑桩基技术规范》式（5.1.1⁃2），扣除承台和其上土重，桩顶面的竖向力设计值为

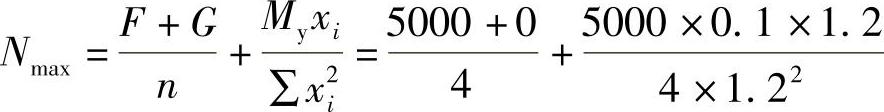
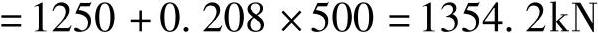
根据《建筑桩基技术规范》式（5.9.2⁃2），承台的最大弯矩设计值为

M_y=∑N_ix_i=2N_i×（1.2-0.4）=2×1354.2×0.8=2166.7kN·m

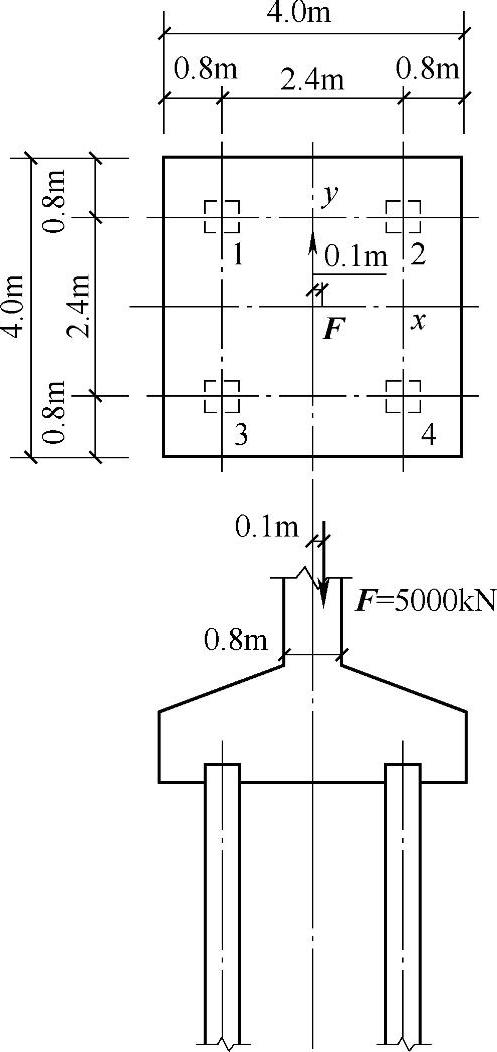
图 9.1.5

【9.1.5】 （2006年二级考题）

有一矩形4桩承台基础，采用沉管灌注桩，桩径为452mm，有效桩长19.10m，有关地基各土层分布情况、桩端端阻力特征值q_pk、桩侧阻力特征值q_sia及桩的布置、承台尺寸等，均示于图9.1.6中。

假定由柱传至承台的荷载效应由永久荷载效应控制；承台自重和承台上的土重标准值G_k=121kN；在标准组合偏心竖向力作用下，最大单桩竖向力标准值Q_kmax=840kN。试问，该承台的最大弯矩设计值M_y（kN·m），最接近于下列何项数值？

（A）1254 （B）1312 （C）1328 （D）1344

【答案】 （B）

【详解】 根据《建筑桩基技术规范》5.9.2条的规定，扣除承台和其上土重，相应于荷载效应基本组合时的单桩竖向力设计值为

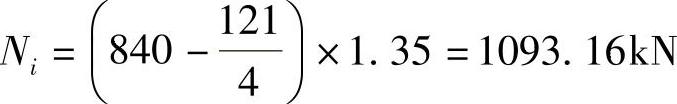
根据《建筑桩基技术规范》式（5.9.2⁃2），承台的最大弯矩设计值为

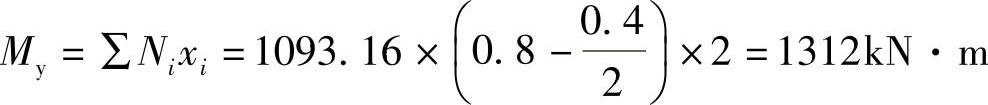，故（B）正确。

【简解】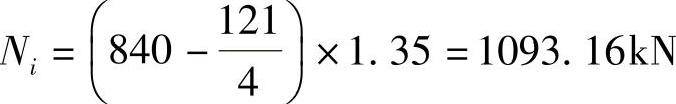 ，则有

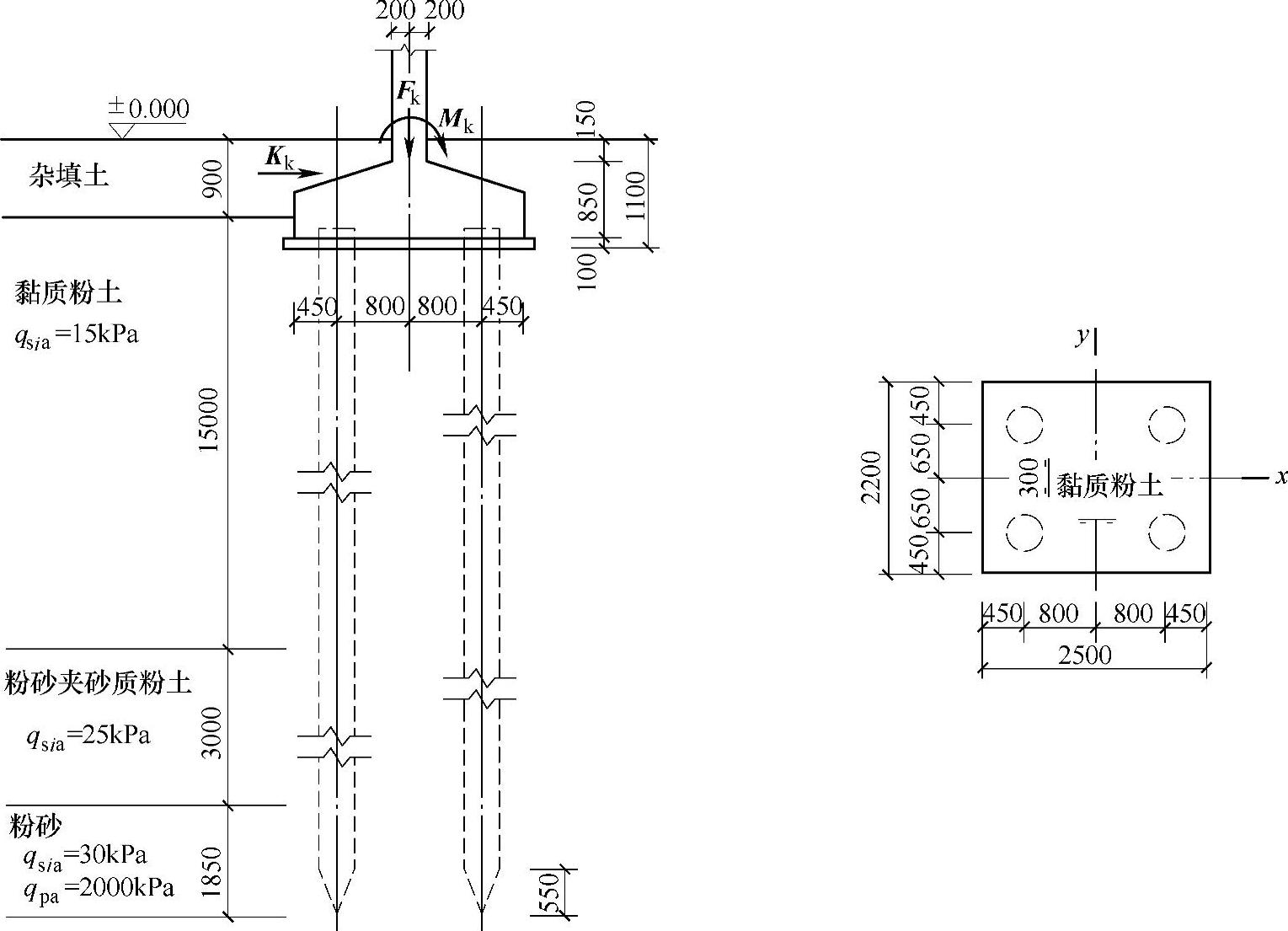
图 9.1.6

【9.1.6】 （2011年岩土考题）

桩基承台如图9.1.7所示（尺寸mm计），已知柱轴力F=12000kN，力矩M=1500kN·m，水平力H=600kN（F、M和H均对应荷载效应基本组合），承台及其上填土的平均重度为20kN/m³。试按《建筑桩基技术规范》计算图示虚线截面处的弯矩设计值，最接近下列哪一组数值？

（A）4800kN·m （B）5300kN·m （C）5600kN·m （D）5900kN·m

【答案】 （C）

【解答】 作用于右桩的竖向力最大，根据《建筑桩基技术规范》式（5.1.1⁃2），扣除承台和其上土重，右桩顶面的竖向力设计值为

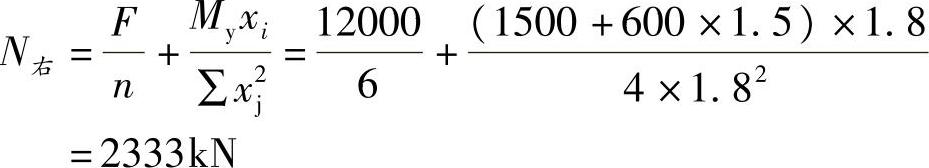
根据《建筑桩基技术规范》式（5.9.2⁃2），承台的最大弯矩设计值为

M_y=∑N_ix_i=2×2333×（1.8-0.6）=5599kN·m

【9.1.7】 （2009年一级考题，原题是连锁题的子题，情境描述有所简化）

某建筑物地基基础设计等级为乙级，其柱下桩基采用预应力高强度混凝土管桩（PHC桩），桩外径400mm，如图9.1.8所示。

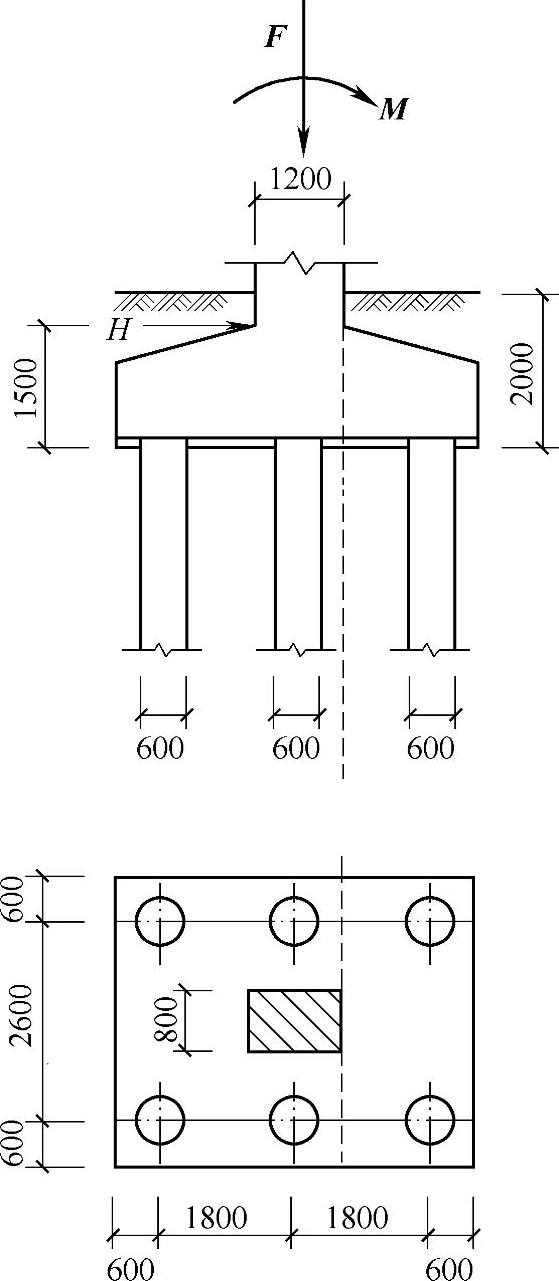
图 9.1.7

取承台及其上土的加权平均重度为20kN/m³。在荷载效应标准组合下，柱传给承台顶面的荷载为：M_k=704kN·m，F_k=4800kN，H_k=60kN。当荷载效应由永久荷载效应控制时，试问，承台在柱边处截面的最大弯矩设计值M（kN·m），最接近于下列何项数值？

（A）2880 （B）3240 （C）3890 （D）4370

【答案】 （C）

【详解】 根据《建筑桩基技术规范》5.9.2条的规定，扣除承台和其上土重，相应于荷载效应基本组合时的单桩竖向力设计值为

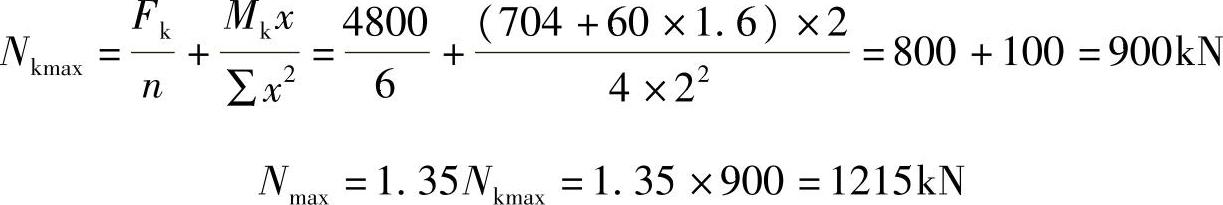
根据《建筑桩基技术规范》5.9.2条（或《建筑地基基础设计规范》8.5.18条）：

M_max=∑N_maxx_i=2×1215×（2-0.4）=3888kN·m

【简解】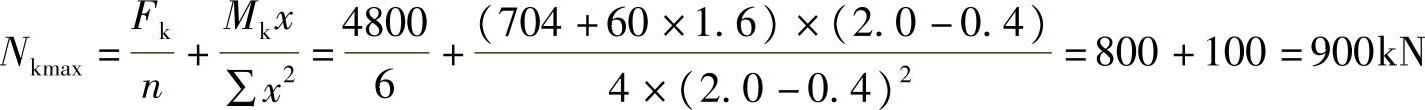

设计值为N_max=1.35N_kmax=1.35×900=1215kN，则有

M_max=∑N_maxx_i=2×1215×（2-0.4）=3888kN·m

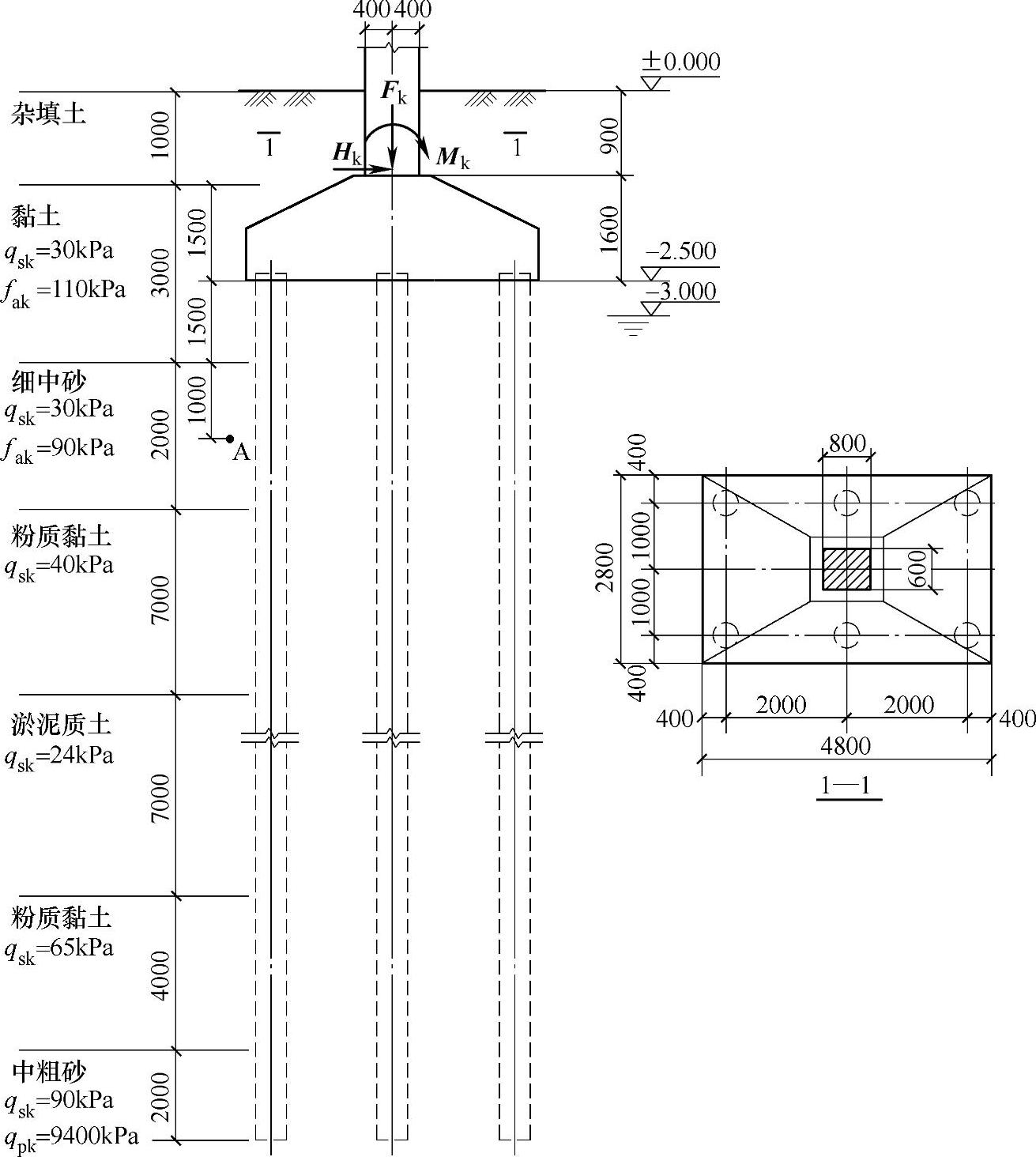
图 9.1.8

【9.1.8】 （2003年二级考题，原题是连锁题的子题，情境描述有所简化）

某柱下桩基础采用6根沉管灌注桩，桩身设计直径d=388mm。如图9.1.9所示。作用于承台顶面的外力有相应于荷载效应标准组合时的竖向力F_k、力矩M_k、水平力H_k。柱截面尺寸为350mm×400mm。

假定F_k=1912kN，M_k=0，H_k=0，承台自重及其上土的自重标准值G_k=3240kN。试问，当按承载能力极限状态下永久荷载效应控制的基本组合（采用简化规则）计算承台内力时，承台的最大弯矩设计值M（kN·m）最接近于下列何项数值？

（A）788.70 （B）1064.75 （C）828.53 （D）1118.52

【答案】 （D）

【详解】 做题提示：求承台最大弯矩时，应分别求出x轴的弯矩和y轴的弯矩，比较以后得到最大值。另外还需注意标准值与设计值的转换。

根据《建筑桩基技术规范》5.9.2条的规定，扣除承台和其上土重，相应于荷载效应基本组合时的单桩竖向力设计值为

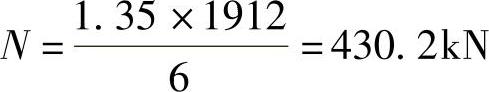
垂直y轴方向自桩轴线到柱边的距离为

x=1.5-0.4/2=1.5-0.2=1.3m

根据《建筑桩基技术规范》式（5.9.2⁃2），承台绕y轴的弯矩设计值为

M_y=N·x·2=430.2×1.30×2=1118.52kN垂直x轴方向自桩轴线到柱边的距离为x=1.0-0.35/2=1.0-0.175=0.825m根据《建筑桩基技术规范》式（5.9.2⁃1），承台绕x轴的弯矩设计值为

M_x=430.2×0.825×3=1064.75kN

所以最大弯矩值为M_y=1118.52kN

故（D）正确。

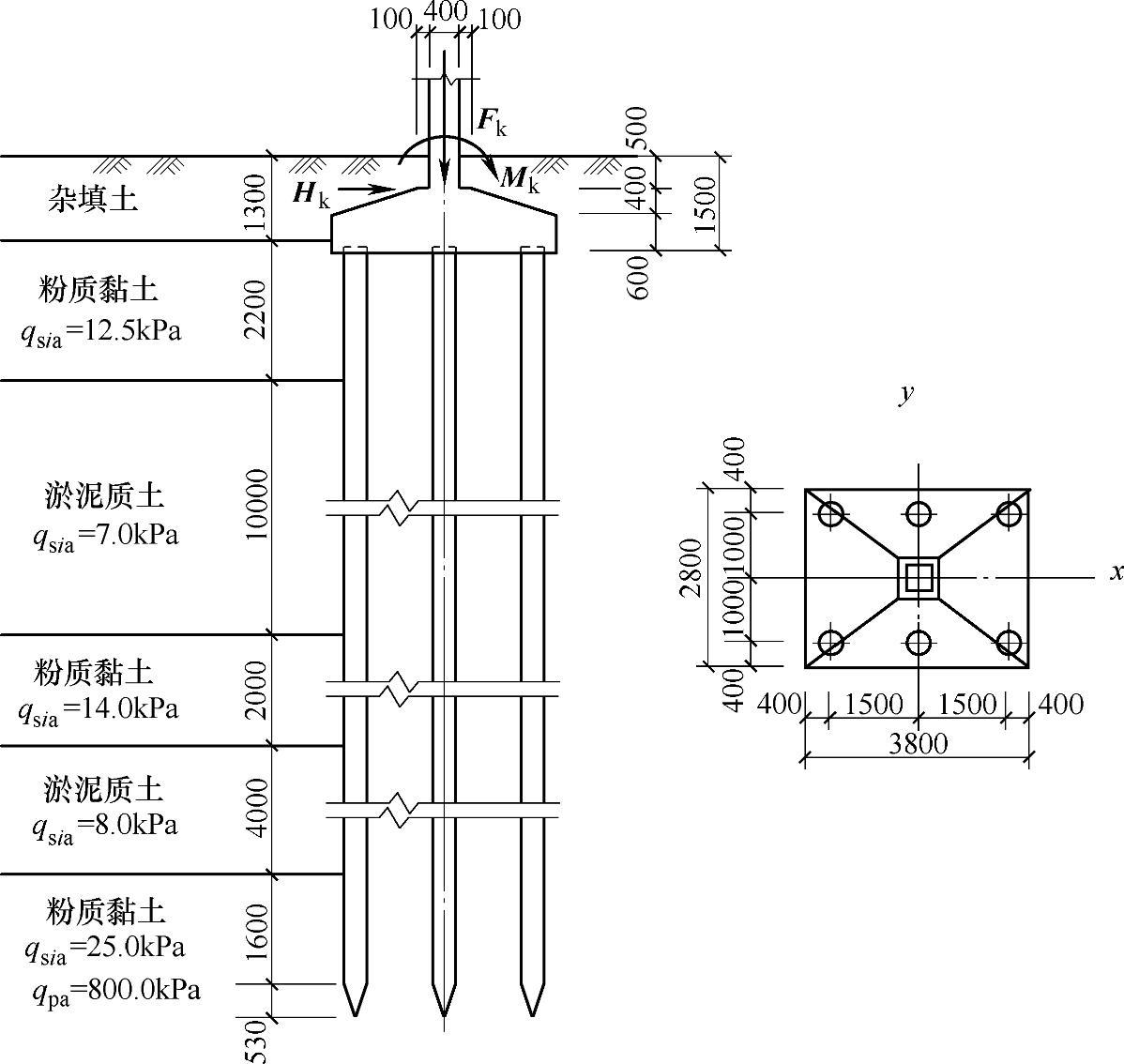
图 9.1.9

【简解】 单桩竖向力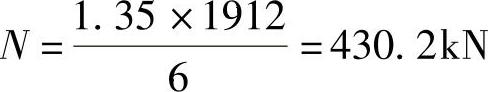

M_y=430.2×（1.5-0.2）×2=1118.52kN·m

M_x=430.2×（1.0-0.175）×3=1064.75kN·m

故最大弯矩值为M_y=1118.52kN·m

【9.1.9】 （2010年二级考题）

某建筑物的地基基础设计为乙级，采用柱下桩基，工程桩采用泥浆护壁钻孔灌注桩，桩径d为650mm。相应于荷载效应标准组合时，由上部结构传至基础顶面的竖向力F_k为10000kN，力矩M_xk为1200kN·m，M_yk为0；相应于荷载效应基本组合时，由上部结构传至基础顶面的竖向力F为13000kN，力矩M_x为1560kN·m，M_y为0；基础及其上土的加权平均重度为20kN/m³，承台及方柱的尺寸、桩的布置以及各土层的地质情况如图9.1.10所示。

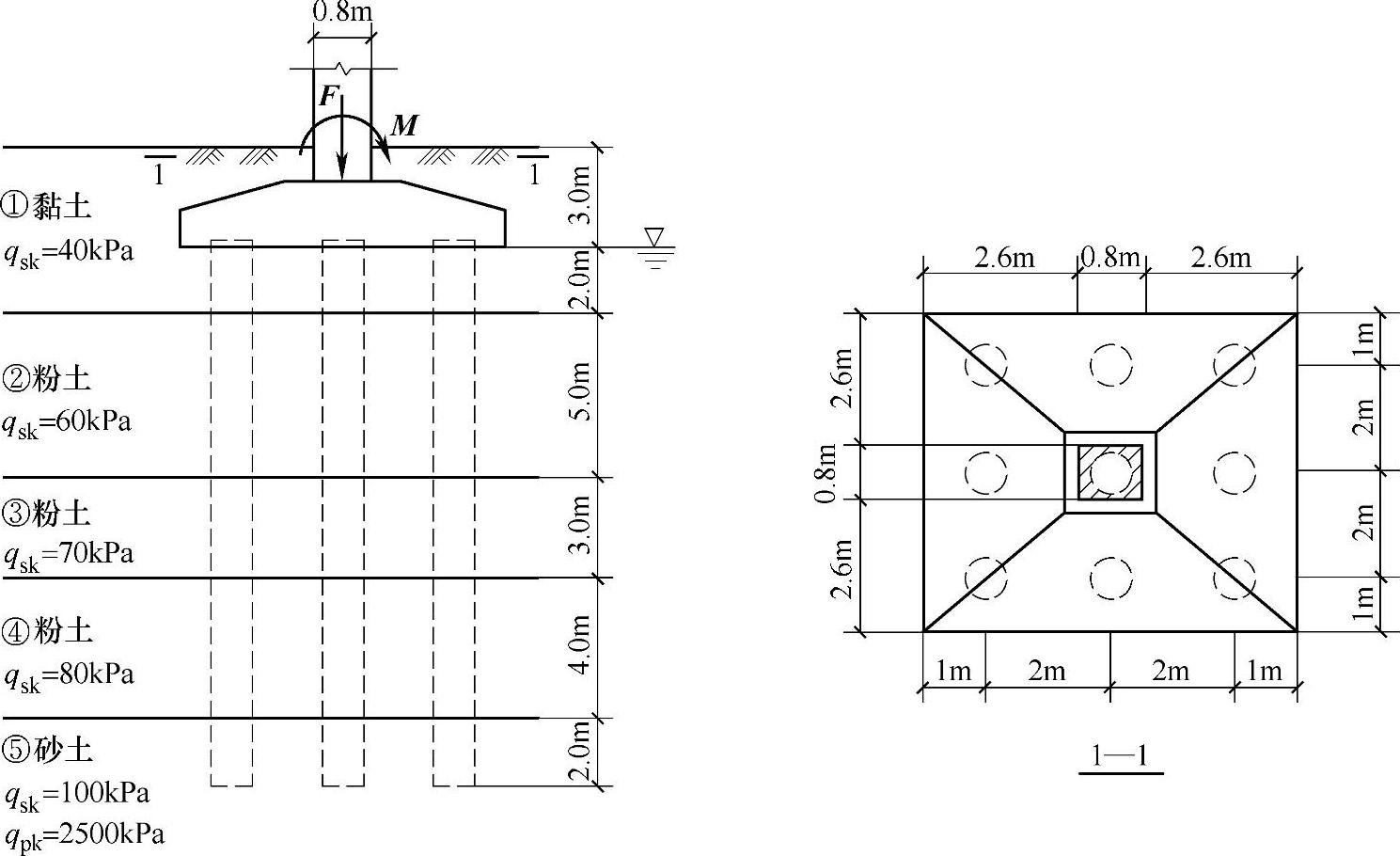
图 9.1.10

桩基承台受弯计算时的最大弯矩设计值M_max（kN·m），与下列何项数值最为接近？

（A）5300 （B）5800 （C）6500 （D）7600

【答案】 （D）

【详解】 根据《建筑桩基技术规范》5.9.2条的规定，相应于荷载效应基本组合时的单桩竖向力设计值为

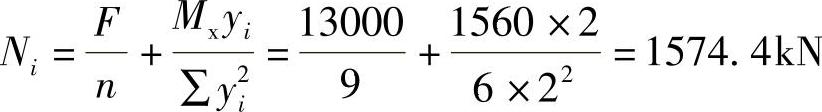
弯矩由三根桩的竖向净反力构成，由桩的中心至计算截面的距离为1.60m，根据《建筑桩基技术规范》式（5.9.2⁃1），承台的最大弯矩设计值为

M_x=∑N_iy_i=3×1574.4×1.6=7557kN·m

故（D）正确。

【简解】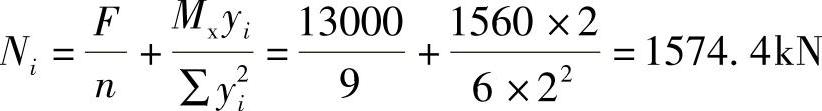 ，则有M_x=∑N_iy_i=3×1574.4×1.6=7557kN·m

【9.1.10】 （2001年一级考题，原题是连锁题的子题，情境描述有所简化）

某承重柱下采用干作业钻孔灌注桩9桩独立基础，其桩长、桩径、承台尺寸及工程地质情况如图9.1.11所示。桩基承台和承台上土自重设计值G=520kN。

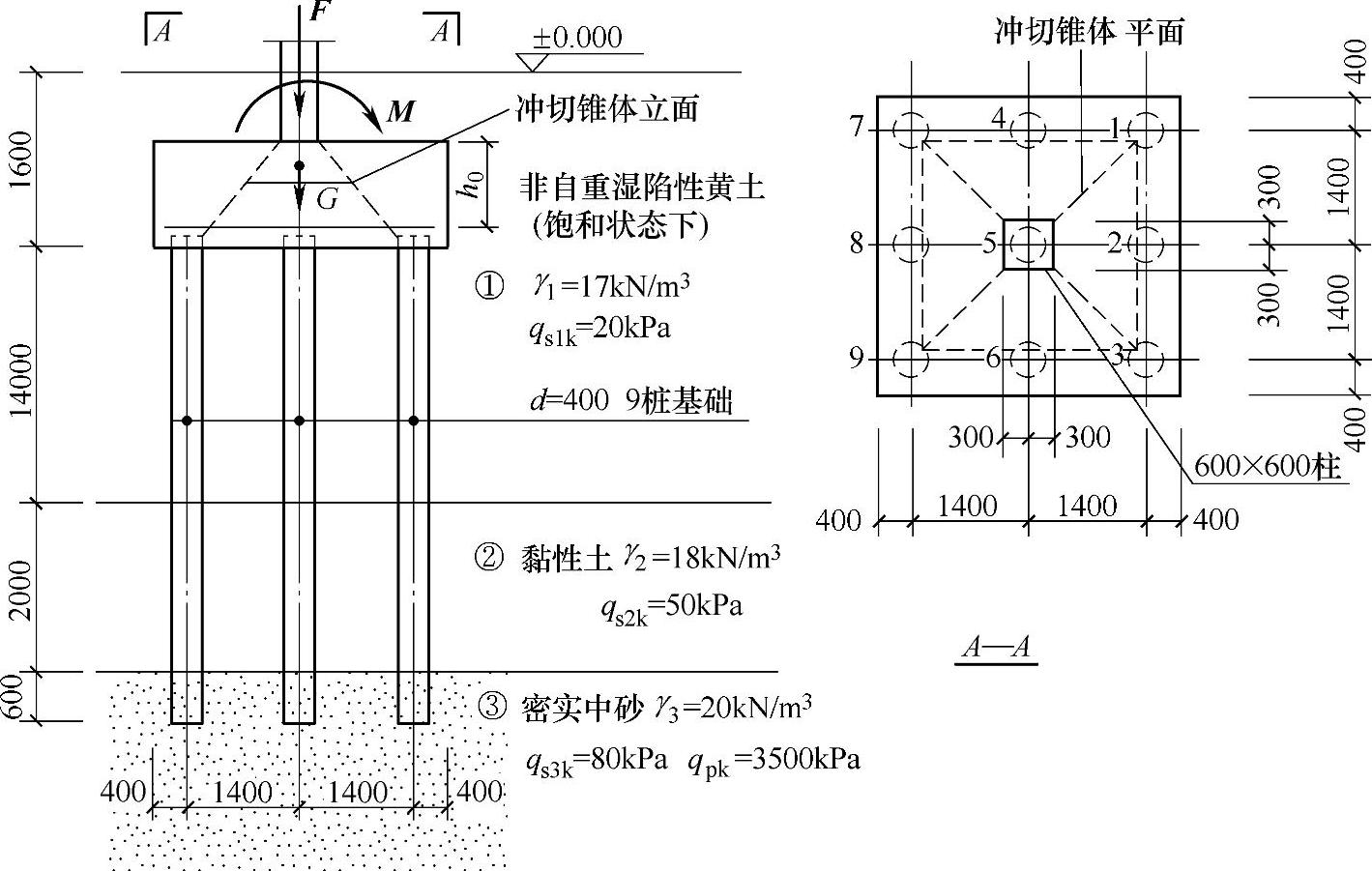
图 9.1.11

假设在图9.1.12中的柱底传力作用下，求得基桩的竖向总反力设计值N₁=N₂=N₃=701kN，N₄=N₅=N₆=584kN，N₇=N₈=N₉=467kN。扣除承台和承台上土自重后，基桩的竖向净反力设计值为N₁=N₂=N₃=643kN，N₄=N₅=N₆=526kN，N₇=N₈=N₉=409kN。试确定矩形承台不利截面的最大弯矩设计值（kN·m）最接近下列何项数值？

（A）1735.8 （B）1927.2 （C）2121.9 （D）2526.2

【答案】 （C）

【详解】 最不利截面位于桩1、2、3一侧的柱边缘，根据《建筑桩基技术规范》式（5.9.2⁃2），承台的最大弯矩设计值为

M_y=∑N_ix_i=643×（1.4-0.3）×3=2121.9kN·m

故（C）正确。

【简解】M_y=∑N_ix_i=643×（1.4-0.3）×3=2121.9kN·m

2.配筋计算

《建筑桩基技术规范》规定：

5.9.1 桩基承台应进行正截面受弯承载力计算。承台弯距可按本规范第5.9.2～5.9.5条的规定计算，受弯承载力和配筋可按现行国家标准《混凝土结构设计规范》GB 50010的规定进行。

4.2.3 承台的钢筋配置应符合下列规定：

1 柱下独立桩基承台的最小配筋率不应小于0.15%。

2 承台底面钢筋的混凝土保护层厚度，当有混凝土垫层时，不应小于50mm，无垫层时不应小于70mm；此外尚不应小于桩头嵌入承台内的长度。

即按下式计算配筋面积A_s

A_s=M/（0.9f_yh₀） （9.1.1）

式中 M——计算截面的弯矩设计值；

f_y——钢筋抗拉强度设计值；

h₀——承台的有效高度。

【9.1.11】 承台纵筋计算

条件：某桩基础承台，基本情况如图9.1.12所示。

（1）几何参数

承台边缘至桩中心距C=500mm，承台根部高度H=1000mm，承台端部高度h=1000mm，纵筋合力重心到底边的距离a_s=70mm，承台埋深h_m=1.50m，矩形柱截面宽B_c=600mm，高H_c=400mm，圆桩直径D_s=500mm。

（2）荷载设计值（作用在承台顶部）

竖向荷载F=4000.00kN，x向剪力V_x=100.00kN，y向剪力V_y=0kN，绕x轴弯矩M_x=0，绕y轴弯矩M_y=600.00kN·m。

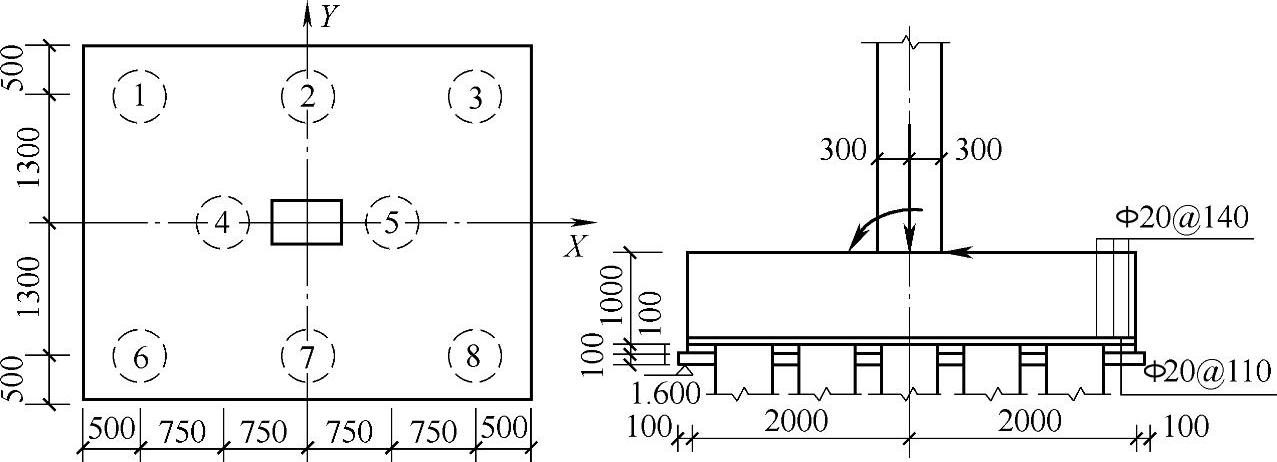
图9.1.12 桩基础设计示意图（单位：mm）

（3）材料

混凝土强度等级：C20，f_c=9.60N/mm²，f_t=1.10N/mm²，钢筋HPB235级，f_y=210.00N/mm²。

要求：计算纵向钢筋A_s值。

【解答】 （1）作用在承台底部的弯矩

绕x轴弯矩：M_0x=0

绕y轴弯矩：M_0y=M_y+V_xh=600.00+100.00×1.00=700.00kN·m

（2）基桩净反力设计值：

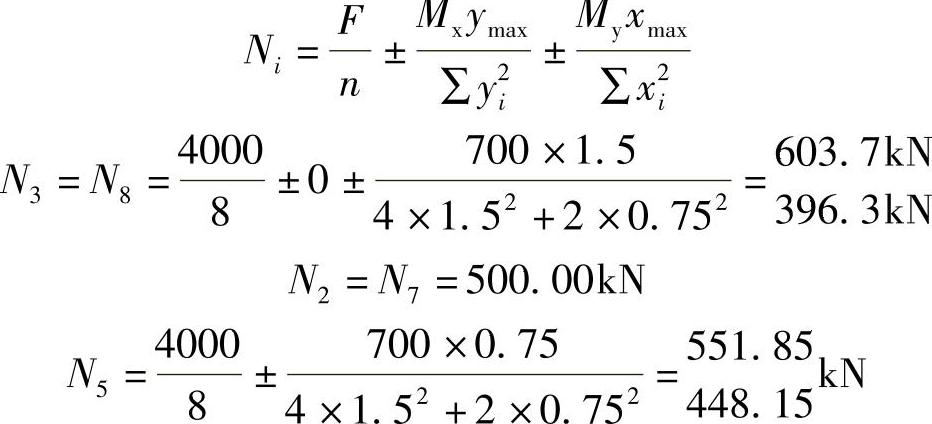
（3）承台受弯计算

1）垂直x轴方向计算截面处弯矩计算

垂直x轴方向计算截面处弯矩设计值（算到柱边）：

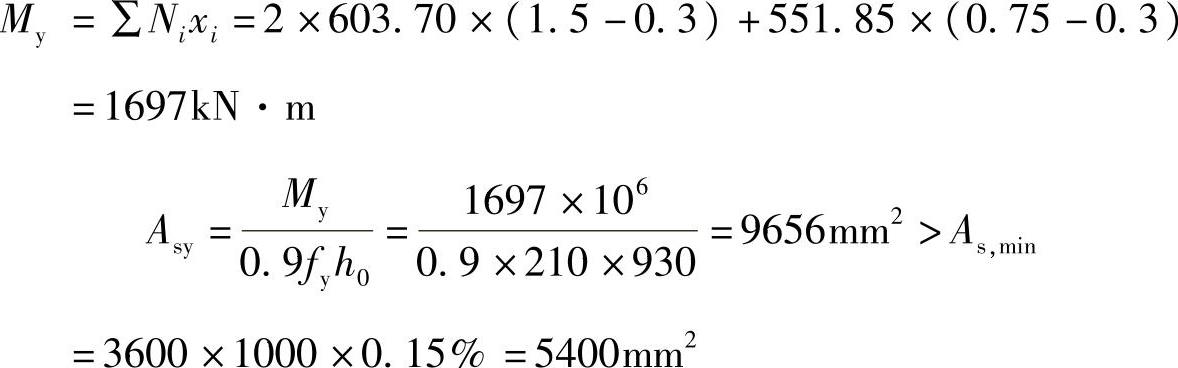
2）垂直y轴方向计算截面处弯矩计算垂直y轴方向计算截面处弯矩设计值：

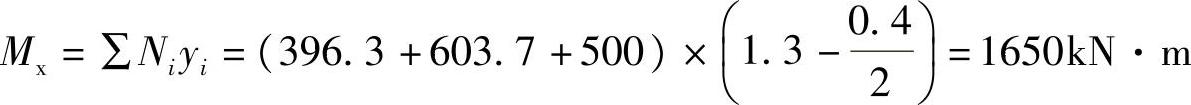
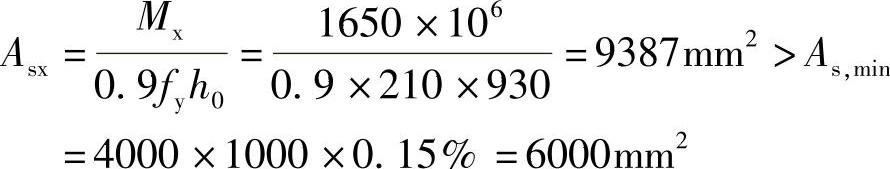
（二）冲切计算

承台的冲切强度有两种，一种是柱对承台自上而下的冲切，一种是桩顶竖向净反力对承台自下而上的冲切。

（1）柱对承台自上而下的冲切

承台在承受柱传来的荷载时，若承台厚度不够，就会发生如图9.1.13所示的冲切破坏，在柱子四周形成一个不大于45°的斜面冲切破坏锥体。对矩形截面柱的矩形承台，在柱与承台交接处以及承台变阶处的冲切强度，可按《建筑桩基技术规范》5.9.7条的规定公式计算：

对于圆柱和圆桩，计算时应将截面换算成方柱，即换算柱截面边宽b_c=0.8d_c，换算桩截面边宽b₀=0.8d₀，此处d_c和d₀为柱和桩的直径。

《建筑桩基技术规范》规定：

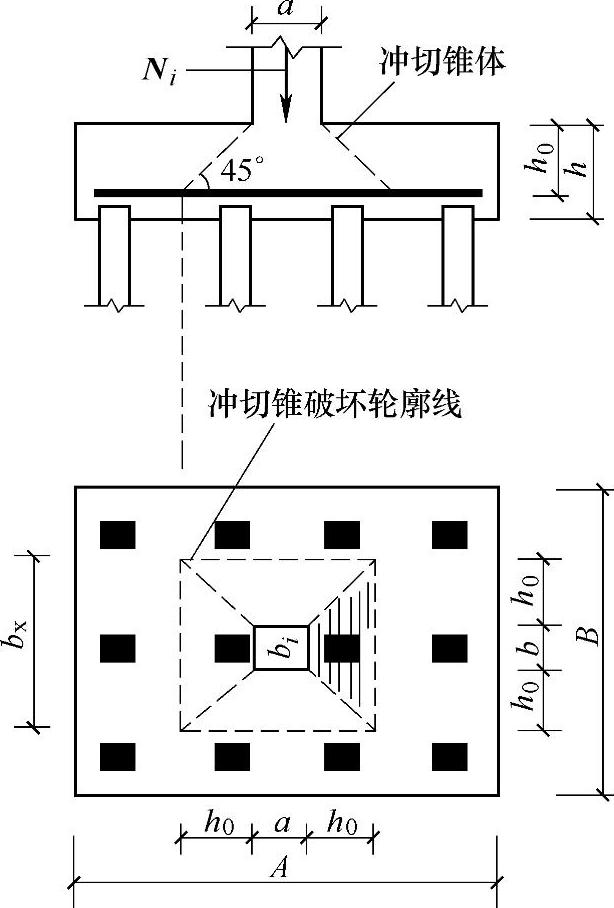
图9.1.13 冲切简图

5.9.6 桩基承台厚度应满足柱（墙）对承台的冲切和基桩对承台的冲切承载力要求。

5.9.7 轴心竖向力作用下桩基承台受柱（墙）的冲切，可按下列规定计算：

1 冲切破坏锥体应采用自柱（墙）边或承台变阶处至相应桩顶边缘连线所构成的锥体，锥体斜面与承台底面之夹角不应小于45°（见图5.9.7）。

2 受柱（墙）冲切承载力可按下列公式计算：

F_l≤β_hpβ₀u_mf_th₀ （5.9.7⁃1）

F_l=F-∑Q_i （5.9.7⁃2）

式中 F_l——不计承台及其上土重，在荷载效应基本组合下作用于冲切破坏锥体上的冲切力设计值；

f_t——承台混凝土抗拉强度设计值；

β_hp——承台受冲切承载力截面高度影响系数，当h≤800mm时，β_hp取1.0，h≥2000mm时，β_hp取0.9，其间按线性内插法取值；

u_m——承台冲切破坏锥体一半有效高度处的周长；

h₀——承台冲切破坏锥体的有效高度；

β₀——柱（墙）冲切系数；

λ——冲跨比，λ=a₀/h₀，a₀为柱（墙）边或承台变阶处到桩边水平距离；当λ<0.25时，取λ=0.25；当λ>1.0时，取λ=1.0；

F——不计承台及其上土重，在荷载效应基本组合作用下柱（墙）底的竖向荷载设计值；

∑Q_i——不计承台及其上土重，在荷载效应基本组合下冲切破坏锥体内各基桩或复合基桩的反力设计值之和。

3 对于柱下矩形独立承台受柱冲切的承载力可按下列公式计算（图5.9.7）：

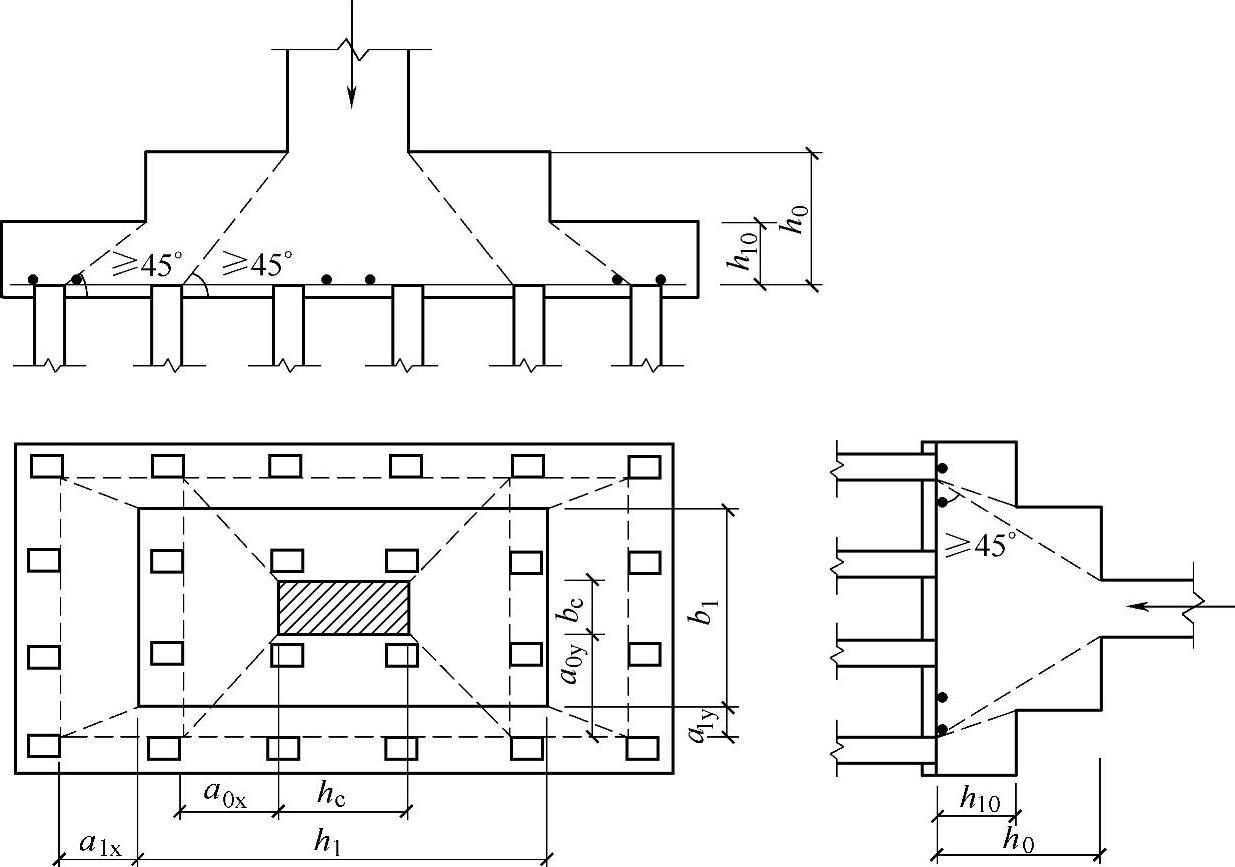
图5.9.7 柱对承台的冲切计算示意

F_l≤2[β_0x（b_c+a_0y）+β_0y（h_c+a_0x）]β_hpf_th₀ （5.9.7⁃4）

式中 β_0x、β_0y——由式（5.9.7⁃3）求得，λ_0x=a_0x/h₀，λ_0y=a_0y/h₀；λ_0x、λ_0y均应满足0.25～1.0的要求；

h_c、b_c——x、y方向的柱截面的边长；

a_0x、a_0y——x、y方向柱边至最近桩边的水平距离。

4 对于柱下矩形独立阶形承台受上阶冲切的承载力可按下列公式计算（图5.9.7）：

F_l≤2[β_1x（b₁+a_1y）+β_1y（h₁+a_1x）]β_hpf_th₁₀ （5.9.7⁃5）

式中 β_1x、β_1y——由式（5.9.7⁃3）求得，λ_1x=a_1x/h₁₀，λ_1y=a_1y/h₁₀；λ_1x、λ_1y均应满足0.25～1.0的要求；

h₁、b₁——x、y方向承台上阶的边长；

a_1x、a_1y——x、y方向承台上阶边至最近桩边的水平距离。

对于圆柱及圆桩，计算时应将其截面换算成方柱及方桩，即取换算柱截面边长b_c=0.8d_c（d_c为圆柱直径），换算桩截面边长b_p=0.8d（d为圆桩直径）。

对于柱下两桩承台，宜按深受弯构件（l₀/h<5.0，l₀=1.15l_n，l_n为两桩净距）计算受弯、受剪承载力，不需要进行受冲切承载力计算。

【9.1.12】～【9.1.13】 （2011年二级考题）

某多层框架结构办公楼，上部结构划分为两个独立的结构单元进行设计计算，防震缝处采用双柱方案，缝宽150mm，缝两侧的框架柱截面尺寸均为600mm×600mm，图9.1.14为防震缝处某条轴线上的框架柱及基础布置情况。上部结构柱KZ1和KZ2作用于基础顶部的水平力和弯矩均较小，基础设计时可以忽略不计。

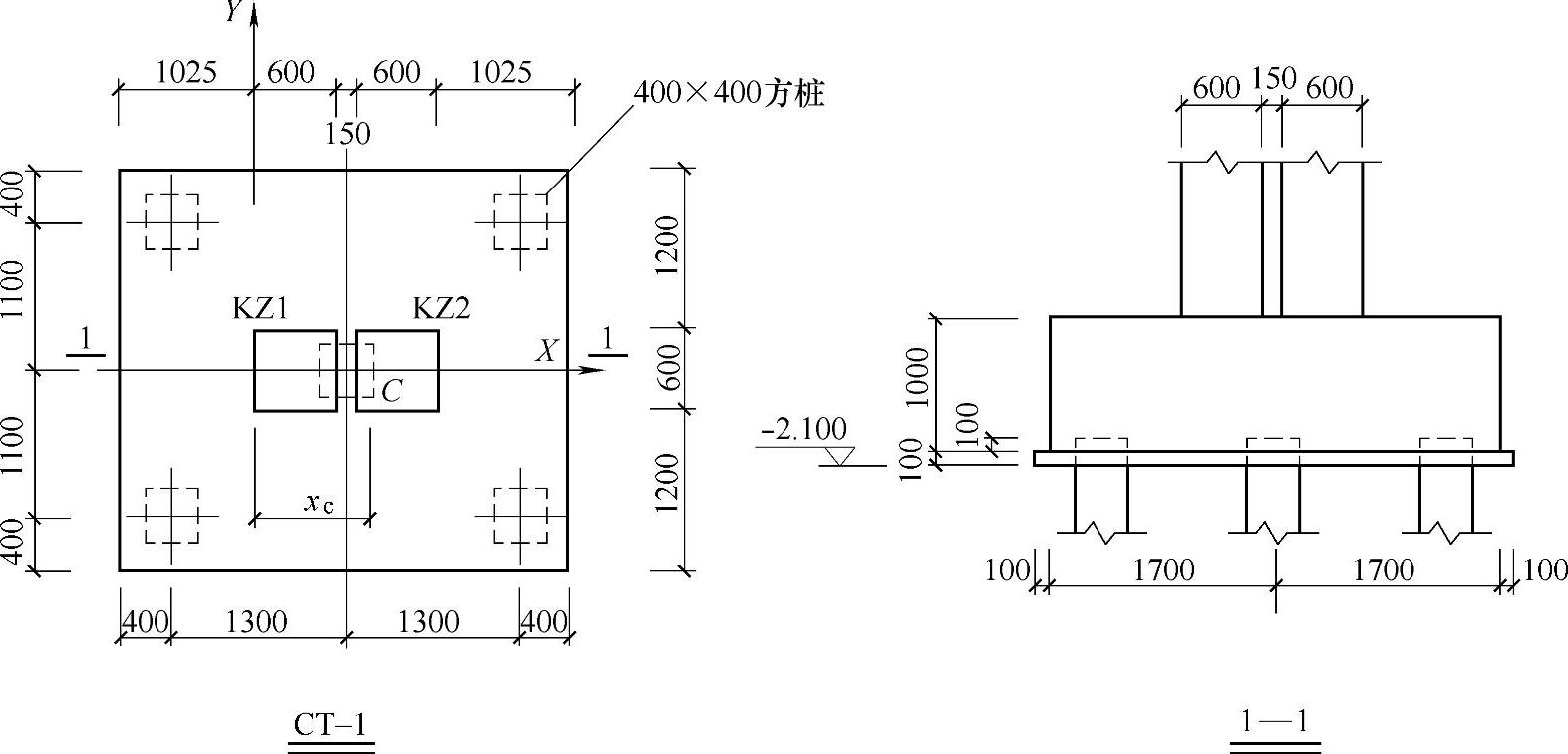
图 9.1.14

【9.1.12】 （2011年二级考题）

对应于某起控制作用的荷载效应标准组合，上部结构柱KZ1和KZ2作用于基础顶部的轴力分别为2160kN和3840kN。试问，在图示参考坐标系下，两柱的竖向力合力作用点位置x_c（mm）与下列何项数值最为接近？

（A）720 （B）740 （C）760 （D）780

【答案】 （D）

【详解】 在图示参考坐标系下，所有的力对y轴位置取矩，有

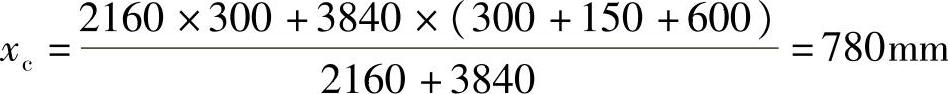
故（D）正确。

【简解】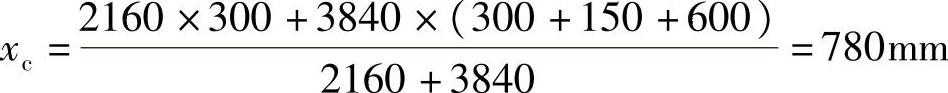

【9.1.13】 （2011年二级考题）

柱KZ1和KZ2采用柱下联合承台，承台下设100mm厚素混凝土垫层，垫层的混凝土强度等级C10；承台混凝土强度等级C30（f_tk=2.01N/mm²，f_t=1.43N/mm²），厚度1000mm，h₀=900mm，桩顶嵌入承台内100mm，假设两柱作用于基础顶部的竖向力大小相同。试问，承台抵抗双柱冲切的承载力设计值（kN）与下列何项数值最为接近？

（A）7750 （B）7850 （C）8150 （D）10900

【答案】 （C）

【详解】 组合柱的截面尺寸为b_c=600mm，h_c=1350mm

根据《建筑桩基技术规范》5.9.7条的规定，承台受冲切承载力截面高度影响系数为

h₀=900，β_hp=1-0.1/6=0.9833

x、y方向柱边至最近桩边的水平距离为

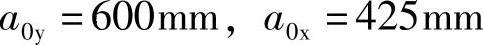
承台冲跨比为

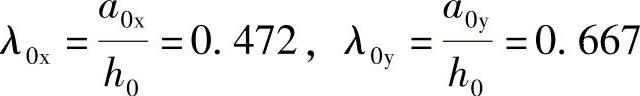
柱冲切系数为

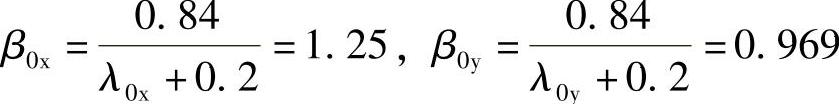
根据《建筑桩基技术规范》式（5.9.7⁃4），承台抵抗双柱冲切的承载力设计值为

2[β_0x（b_c+a_0y）+β_0y（h_c+a_0x）]β_hpf_th₀

=2×[1.25×（600+600）+0.969×（1350+425）]×0.9833×1.43×900×10^-3

=8149.8kN，故（C）正确。

【简解】 2[β_0x（b_c+a_0y）+β_0y（h_c+a_0x）]β_hpf_th₀

=2×[1.25×（600+600）+0.969×（1350+425）]×0.9833×1.43×900×10^-3

=8149.8kN

其中β_hp=1-0.1/6=0.9833

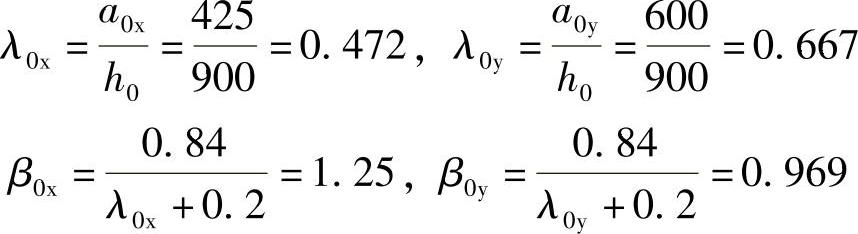
【9.1.14】 （2002年二级考题）

某二级建筑物有一钢筋混凝土柱下桩基础。采用六根沉管灌注桩，桩身设计直径d=426mm，桩端进入持力层（黏性土）的深度为2500mm。作用于桩基承台顶面的外力有竖向力设计值F、力矩设计值M和水平剪力设计值V，承台和承台上的土的平均重度γ_G=20kN/m³。承台平面尺寸和桩位布置，桩基础剖面和地基土层分布状况如图9.1.15所示。

当计算该承台受冲切承载力时。已知承台受力钢筋截面重心至承台底面边缘的距离为60mm，自柱边沿座标x轴方向到最近桩边的距离a_0x=1.08m。自柱边沿座标y轴方向到最近桩边的距离a_0y=0.53m。根据《建筑桩基技术规范》，试判定该承台的冲跨比λ_0x和λ_0y与下列何组数值最为接近？

（A）λ_0x=0.6，λ_0y=0.96 （B）λ_0x=1.0，λ_0y=0.5638

（C）λ_0x=1.1489，λ_0y=0.5638 （D）λ_0x=0.96，λ_0y=0.6

【答案】 （B）

【详解】 根据《建筑桩基技术规范》5.9.7条的规定，承台的冲跨比为

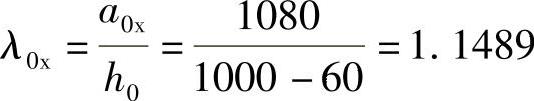，取λ_0x=1.0

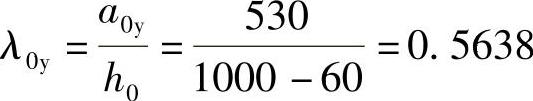
故（B）正确。

【简解】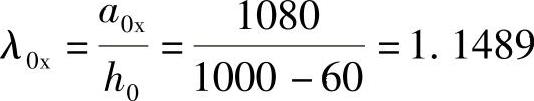 ，取λ_0x=1.0

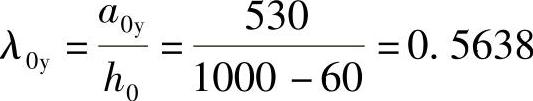
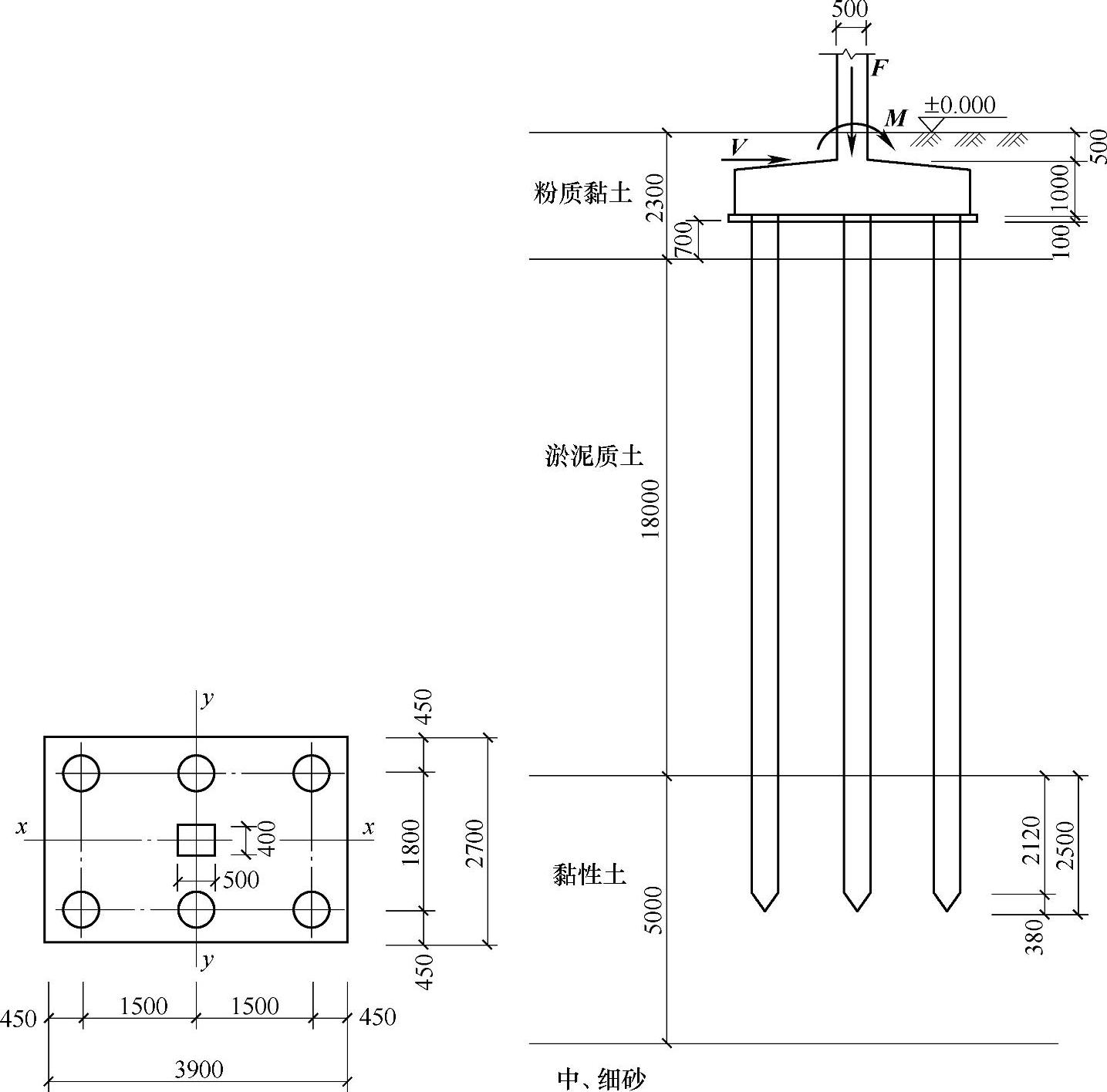
图 9.1.15

【9.1.15】 （2005年二级考题）

柱下钢筋混凝土承台，桩及承台相关尺寸如图9.1.16所示，柱为方柱，居承台中心。柱相应于荷载效应基本组合的轴力设计值N=9500kN；承台采用C40混凝土，混凝土保护层厚度取110mm。

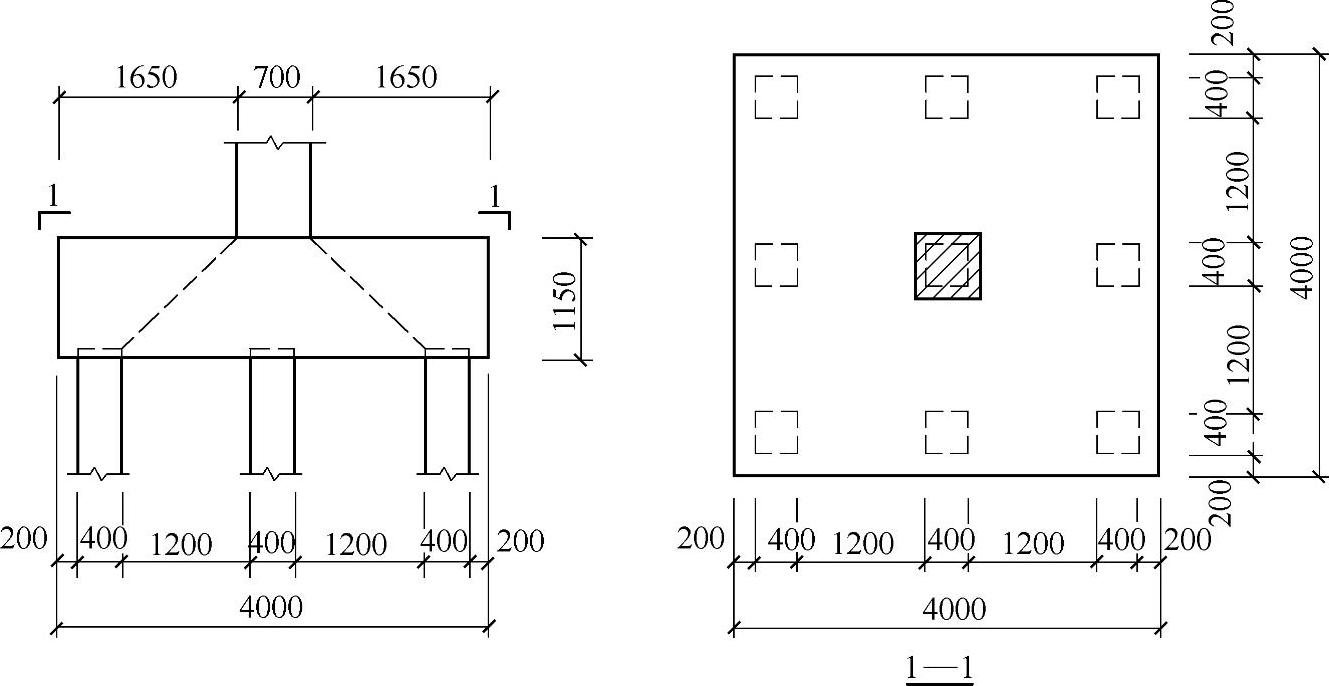
图 9.1.16

已求得β_0x=β_0y=0.6，试问，验算柱对承台的冲切时，承台的抗冲切承载力设计值（kN），与下列何项数值最为接近？

（A）2150 （B）7240 （C）8580 （D）8800

【答案】 （B）

【详解】 根据《建筑桩基技术规范》5.9.7条的规定，承台受冲切承载力截面高度影响系数为

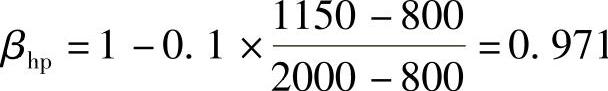
由题意可知

a_0x=a_0y=1050mm，h₀=1040mm，f_t=1.71N/mm²，b_c=h_c=700mm

根据《建筑桩基技术规范》式（5.9.7⁃4），承台抵抗柱冲切的承载力设计值为

2[β_0x（b_c+a_0y）+β_0y（h_c+a_0x）]β_hpf_th₀

=2×2×0.6×（0.700+1.050）×0.971×1.71×10³×（1.150-0.110）

=7241kN

故（B）正确。

【简解】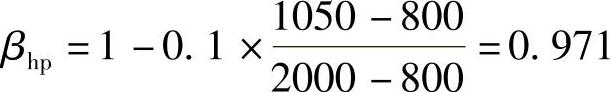

承载力设计值为

2[β_0x（b_c+a_0y）+（h_c+a_0x）]β_hpf_th₀

=2×2×0.6×（0.700+1.050）×0.971×1.71×10³×（1.150-0.110）

=7241kN

【9.1.16】 （2010年二级考题）

某建筑物的地基基础设计为乙级，采用柱下桩基，工程桩采用泥浆护壁钻孔灌注桩，桩径d为650mm。相应于荷载效应标准组合时，由上部结构传至基础顶面的竖向力F_k为10000kN，力矩M_xk为1200kN·m，M_yk为0；相应于荷载效应基本组合时，由上部结构传至基础顶面的竖向力F为13000kN，力矩M_x为1560kN·m，M_y为0；基础及其上土的加权平均重度为20kN/m³，承台及方柱的尺寸、桩的布置以及各土层的地质情况如图9.1.17所示。

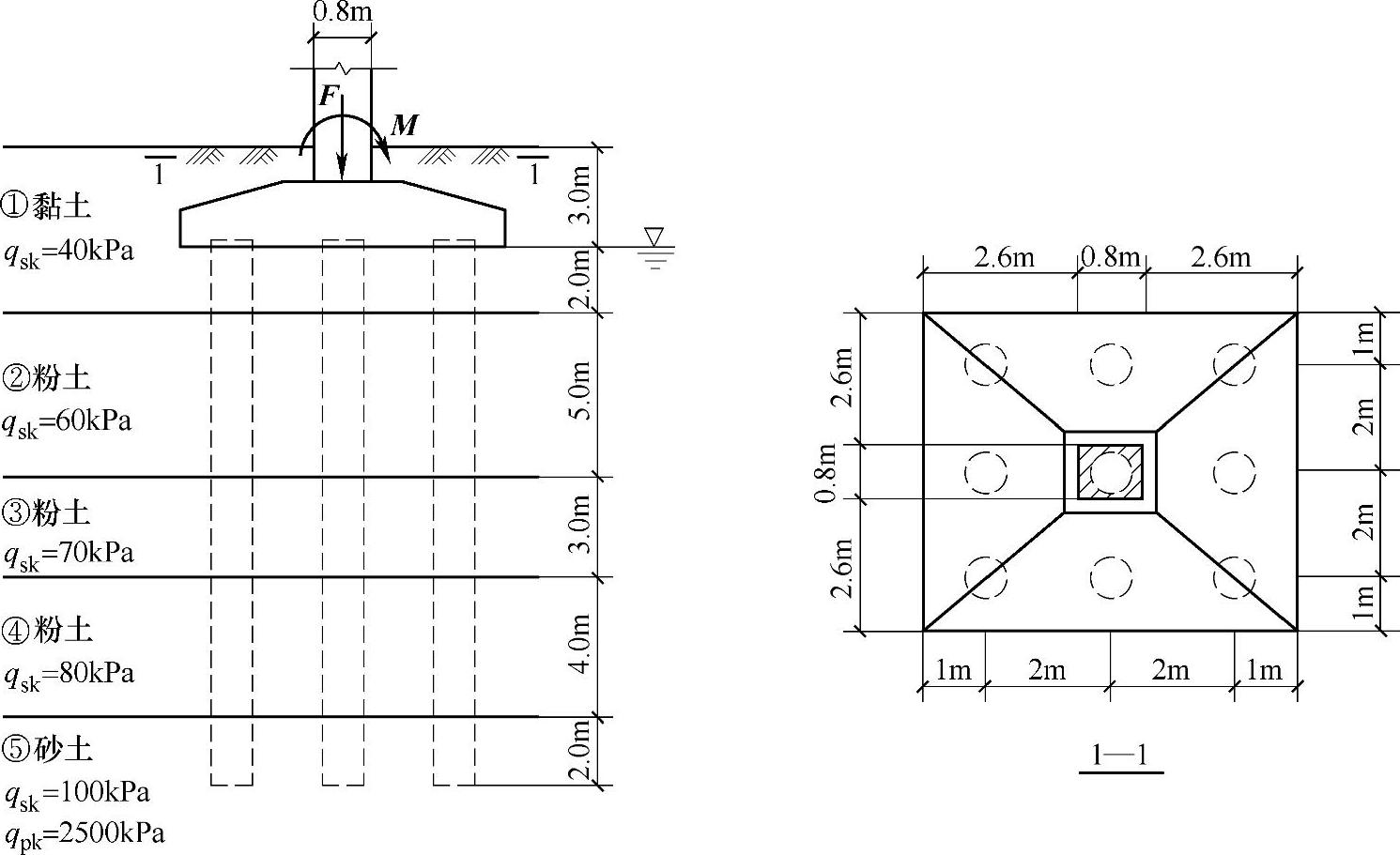
图 9.1.17

验算承台受柱冲切承载力时，假定柱边至四周桩顶内边缘形成的冲切破坏锥体与承台底面的夹角大于45°。试问，该冲切破坏锥体上相应于荷载效应基本组合的冲切力设计值F_l（kN），与下列何项数值最为接近？

（A）6730 （B）8890 （C）11560 （D）13720

【答案】 （C）

【详解】 做题提示：冲切力作用在由柱边至桩顶内边缘形成的冲切破坏锥体上；其值为承台顶面的竖向荷载（不包括承台及其上的土的自重），减去冲切破坏锥体内桩的反力设计值（不包括承台及其上的土的自重）。

根据《建筑桩基技术规范》5.9.7条的规定，冲切破坏锥体上相应于荷载效应基本组合的冲切力设计值为(www.xing528.com)

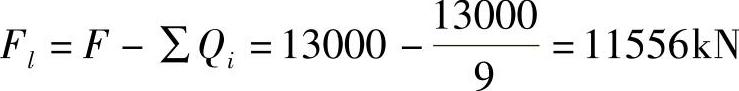
在冲切破坏锥体内的桩只有1根，故其结果为11556kN。故（C）正确。

【简解】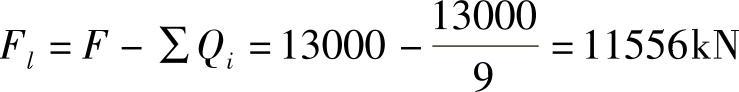

【9.1.17】～【9.1.18】 （2007年一级考题）

某框架结构柱基础，由上部结构传至该柱基的荷载标准值为：F=7600kN，M_x=M_y=800kN·m。柱基础独立承台下采用400mm×400mm钢筋混凝土预制桩，桩的平面布置及承台尺寸如图9.1.18所示。承台底面埋深3.0m，柱截面尺寸为700mm×700mm，居承台中心位置。承台采用C40混凝土，混凝土保护层厚度取50mm。承台及承台以上土的加权平均重度为20kN/m³。

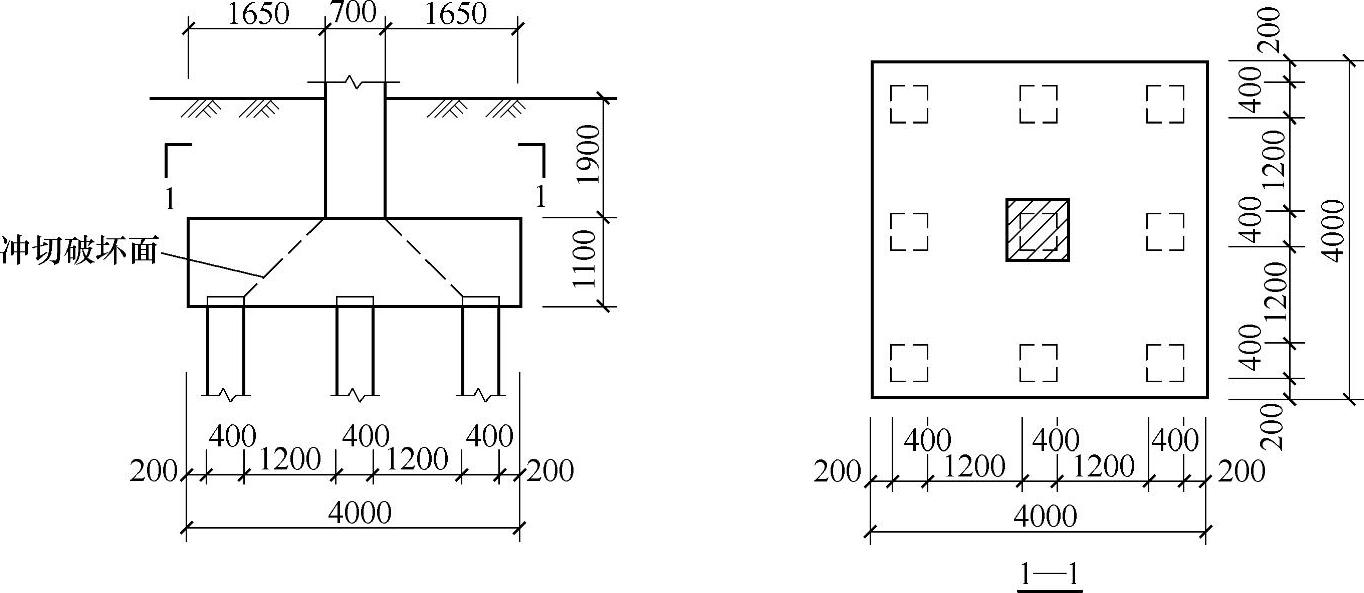
图 9.1.18

【9.1.17】 （2007年一级考题）

假定相应于荷载效应基本组合由永久荷载控制，试问，柱对承台的冲切力设计值F_l（kN），与下列何项数值最为接近？

（A）5870 （B）6720 （C）7920 （D）9120

【答案】 （D）

【详解】 根据《建筑桩基技术规范》5.9.7条的规定，柱对承台的冲切力设计值为

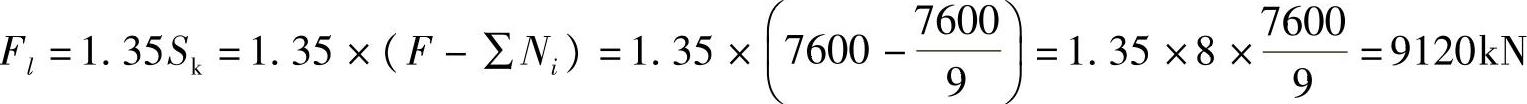
故（D）正确。

【简解】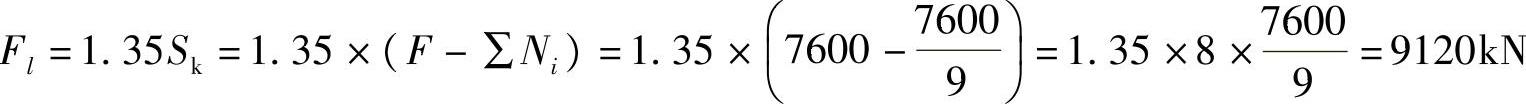

【9.1.18】 （2007年一级考题）

试问，验算柱对承台的冲切时，承台的抗冲切承载力设计值（kN），与下列何项数值最为接近？

（A）2150 （B）4290 （C）8220 （D）8580

【答案】 （D）

【详解】 承台的有效高度为h₀=（1100-50）mm=1050mm

根据《建筑桩基技术规范》5.9.7条的规定，承台受冲切承载力截面高度影响系数为

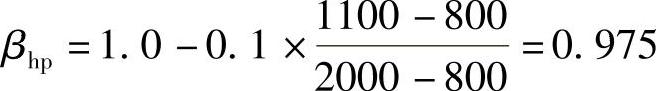
x、y方向柱边至最近桩边的水平距离为

a_0x=a_0y=（1400-350）mm=1050mm，f_t=1.71N/mm²，

承台冲跨比和柱冲切系数为

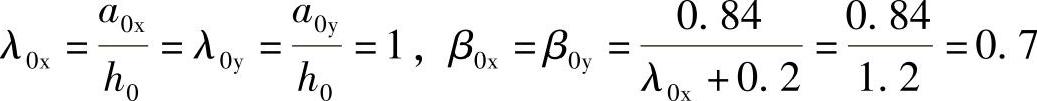
根据《建筑桩基技术规范》式（5.9.7⁃4），承台抵抗柱冲切的承载力设计值为

2[β_0x（b_c+a_0y）+β_0y（h_c+a_0x）]β_hpf_th₀

=2×2×0.7×（700+1050）×0.975×1.71×1050=8578kN

故（D）正确。

【简解】 2[β_0x（b_c+a_0y）+β_0y（h_c+a_0x）]β_hpf_th₀

=2×2×0.7×（700+1050）×0.975×1.71×1050=8578kN

其中

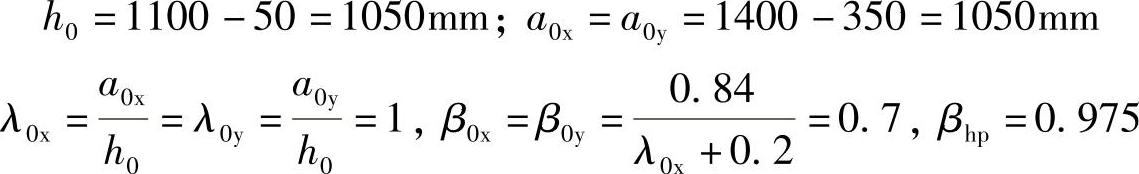
（2）桩对承台的冲切

当承台边缘处的厚度较小时，桩的反力有可能使承台边缘沿45°斜截面产生冲切破坏（图9.1.19）。此时，承台板的抗冲切强度按《建筑桩基技术规范》的5.9.8条的公式计算。

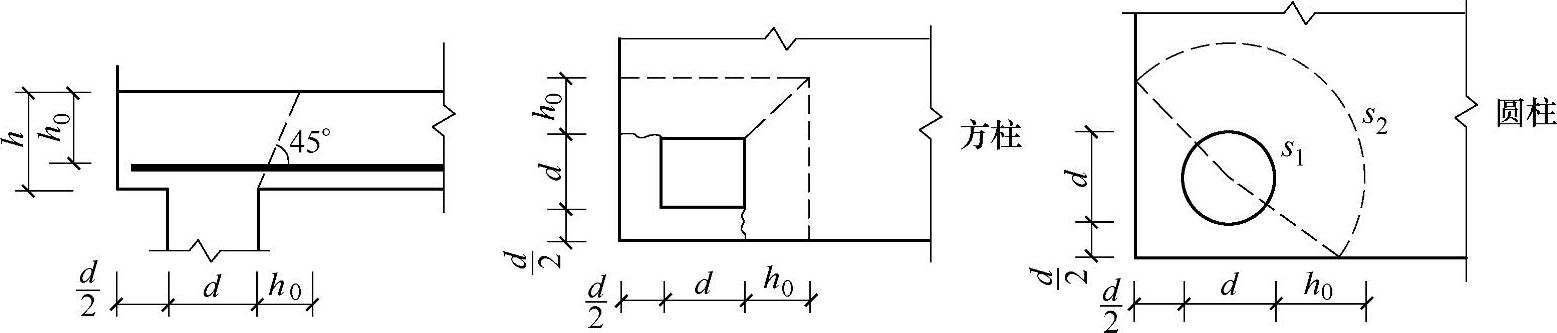
图9.1.19 角桩冲切计算图

《建筑桩基技术规范》规定：

5.9.8 对位于柱（墙）冲切破坏锥体以外的基桩，可按下列规定计算承台受基桩冲切的承载力：

1 四桩以上（含四桩）承台受角桩冲切的承载力可按下列公式计算（见图5.9.8⁃1）：

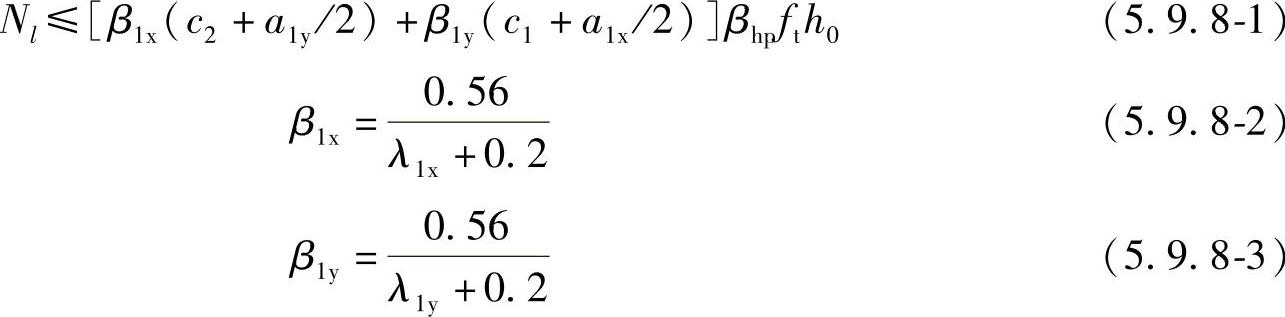
式中 N_l——不计承台及其上土重，在荷载效应基本组合作用下角桩（含复合基桩）反力设计值；

β_1x、β_1y——角桩冲切系数；

a_1x、a_1y——从承台底角桩顶内边缘引45°冲切线与承台顶面相交点至角桩内边缘的水平距离；当柱（墙）边或承台变阶处位于该45°线以内时，则取由柱（墙）边或承台变阶处与桩内边缘连线为冲切锥体的锥线（图5.9.8⁃1）；

h₀——承台外边缘的有效高度；

λ_1x、λ_1y——角桩冲跨比，λ_1x=a_1x/h₀，λ_1y=a_1y/h₀，其值均应满足0.25～1.0的要求。

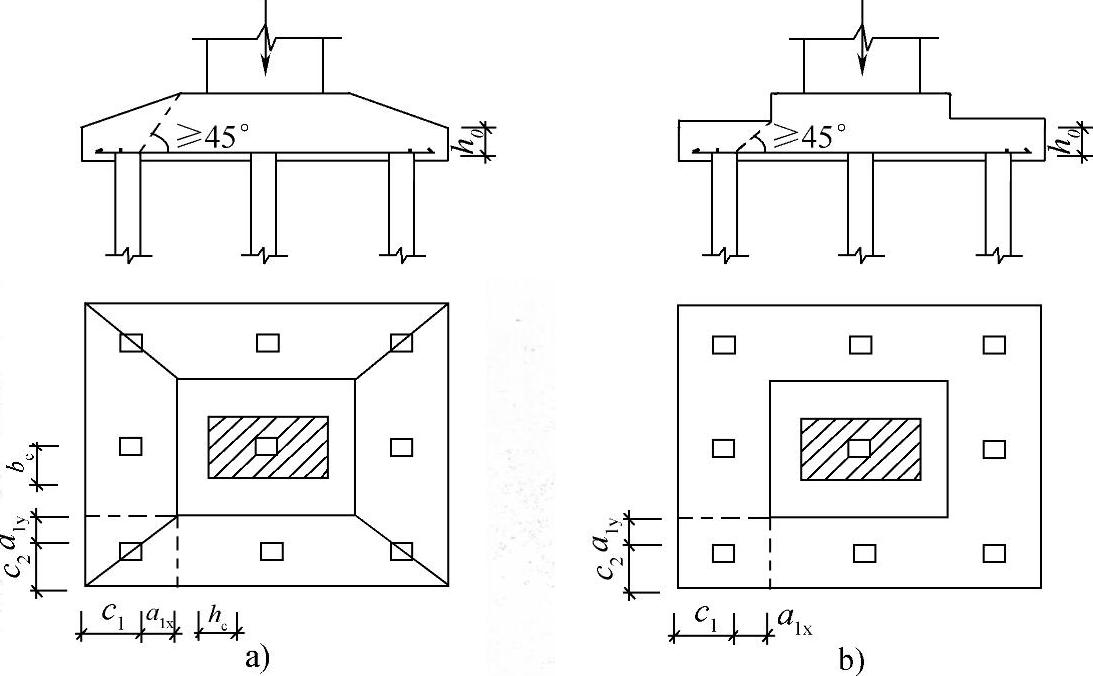
图5.9.8⁃1 四桩以上（含四桩）承台角桩冲切计算示意

a）锥形承台 b）阶形承台

【9.1.19】 （2007年一级考题）

某框架结构柱基础，由上部结构传至该柱基的荷载标准值为：F=7600kN，M_x=M_y=800kN·m。柱基础独立承台下采用400mm×400mm钢筋混凝土预制桩，桩的平面布置及承台尺寸如图9.1.20所示。承台底面埋深3.0m，柱截面尺寸为700mm×700mm，居承台中心位置。承台采用C40混凝土，混凝土保护层厚度取50mm。承台及承台以上土的加权平均重度为20kN/m³。

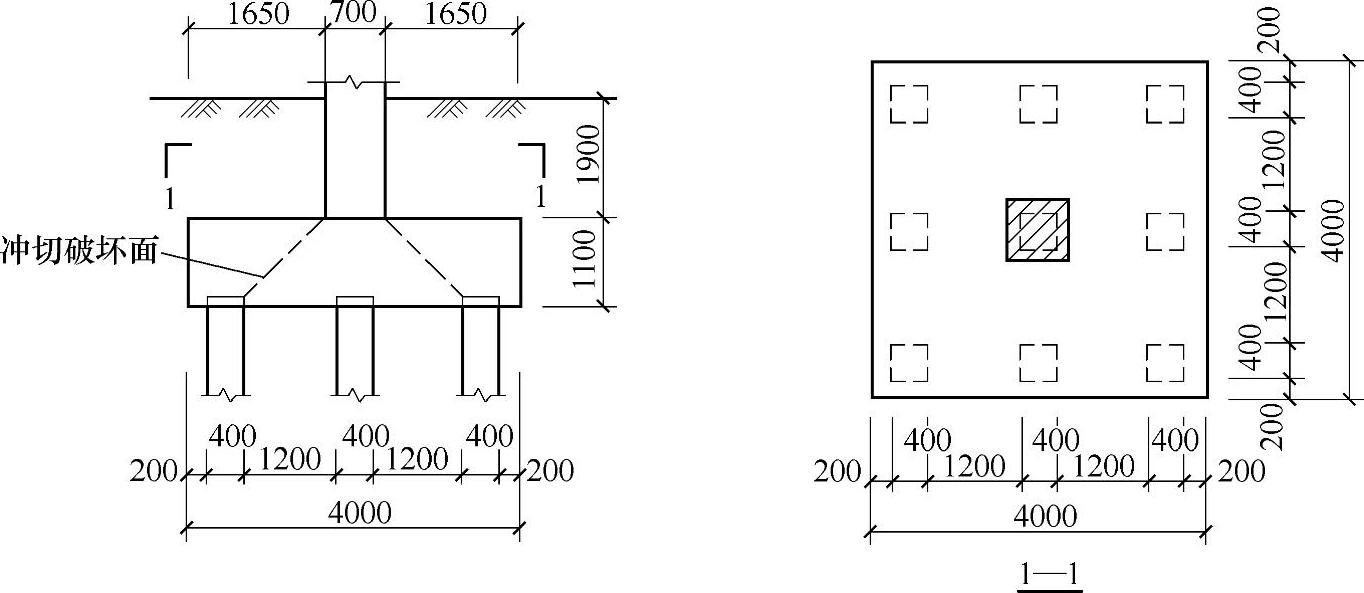
图 9.1.20

验算角桩对承台的冲切时，试问，承台的抗冲切承载力设计值（kN），与下列何项数值最为接近？

（A）880 （B）920 （C）1760 （D）1840

【答案】 （D）

【详解】 根据《建筑桩基技术规范》5.9.8条的规定，从承台底角桩内边缘引45°冲切线与承台顶面相交点至角桩内边缘的水平距离（即承台的有效高度）为

a_1x=a_1y=1050mm

由《建筑桩基技术规范》图5.9.8⁃1和本题图9.1.20，可知c₁=c₂=600mm

角桩冲跨比为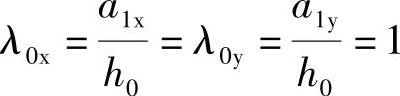

角桩冲切系数为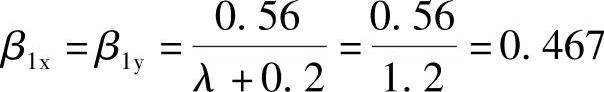

根据《建筑桩基技术规范》式（5.9.8⁃1），承台的抗角桩冲切承载力设计值为

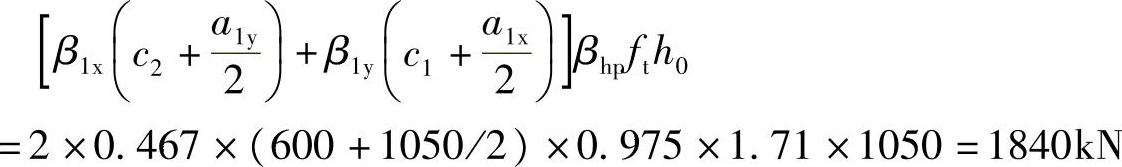
故（D）正确。

【简解】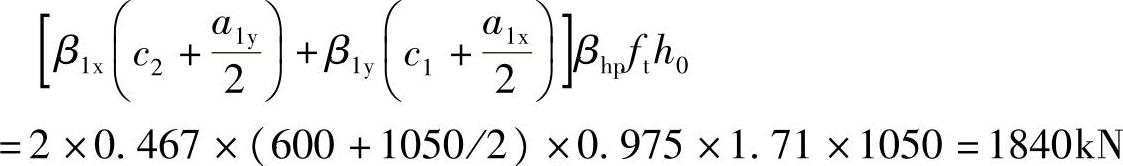

其中a_1x=a_1y=1050mm，c₁=c₂=600mm

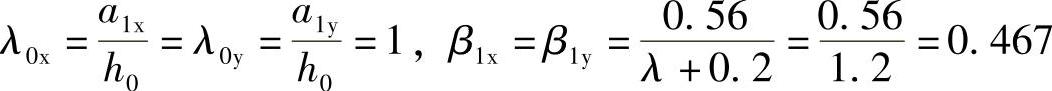
【9.1.20】 （2007年岩土考题）

如图9.1.21所示，某4桩的承台，桩截面尺寸为0.4m×0.4m，预制桩，承台混凝土强度等级C35（f_t=1.57MPa）。试计算角桩冲切承载力。

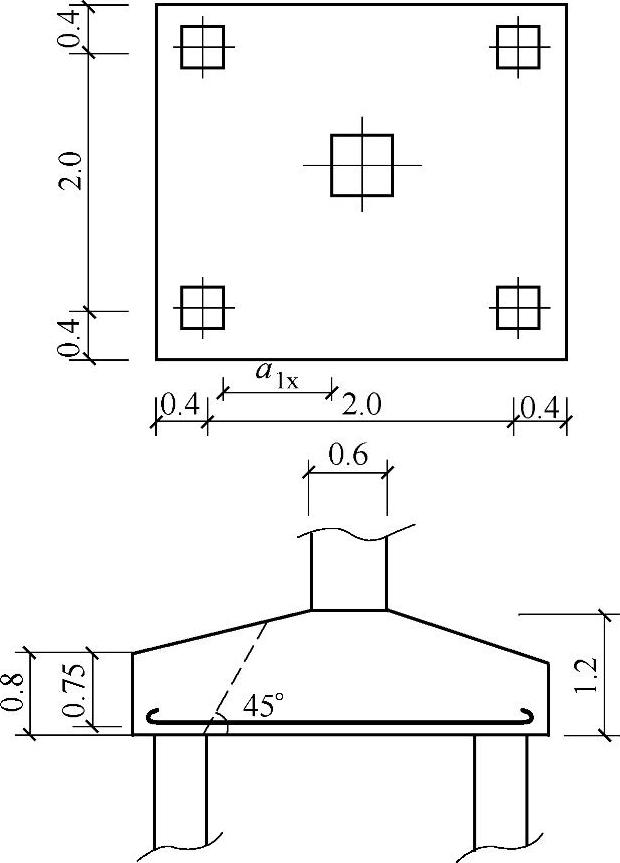
图9.1.21（尺寸单位：m）

【详解】 根据《建筑桩基技术规范》5.9.8条的规定，从承台底角桩内边缘引45°冲切线与承台顶面相交点至角桩内边缘的水平距离为

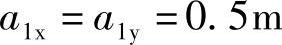
由《建筑桩基技术规范》图5.9.8⁃1和本题图9.1.21，可知c₁=c₂=600mm

角桩冲跨比为

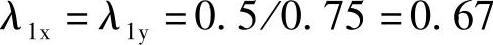
角桩冲切系数为

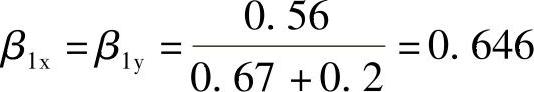
根据《建筑桩基技术规范》式（5.9.8⁃1），承台的抗角桩冲切承载力设计值为

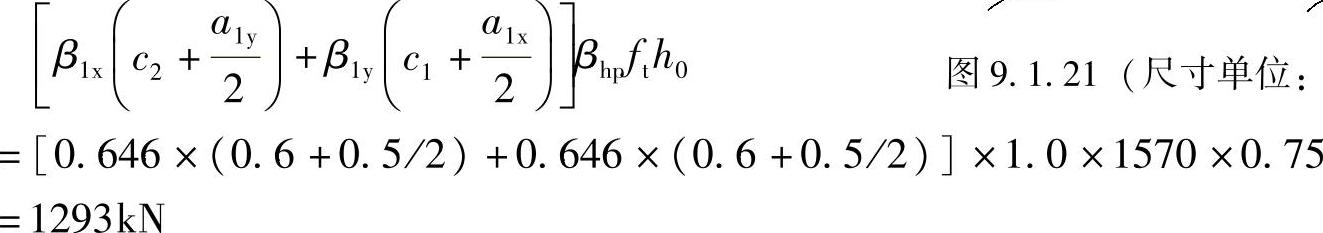
（三）受剪计算

剪切破坏面为荷载作用处与支座间连线所形成的斜截面，即柱边（墙边）和桩边连线所形成的斜截面。应对柱的纵横（x—x，y—y）两个方向的斜截面分别按《建筑桩基技术规范》5.9.9条的规定进行受剪承载力验算。

进行斜截面抗剪计算时应注意以下几点：

①当柱边（墙边）外有多排桩形成多个剪切斜截面时，需对每个斜截面进行验算。

②对阶梯形承台需分别在变阶处及柱边进行斜截面受剪计算。

③对锥形承台需在承台顶斜面与平面交接位置进行斜截面受剪计算。

④墙（柱）下条形承台梁斜截面受剪，根据《混凝土结构设计规范》计算。

《建筑桩基技术规范》规定：

5.9.9 柱（墙）下桩基承台，应分别对柱（墙）边、变阶处和桩边联线形成的贯通承台的斜截面的受剪承载力进行验算。当承台悬挑边有多排基桩形成多个斜截面时，应对每个斜截面的受剪承载力进行验算。

5.9.10 柱下独立桩基承台斜截面受剪承载力应按下列规定计算：

1 承台斜截面受剪承载力可按下列公式计算（见图5.9.10⁃1）

V≤β_hsαf_tb₀h₀ （5.9.10⁃1）

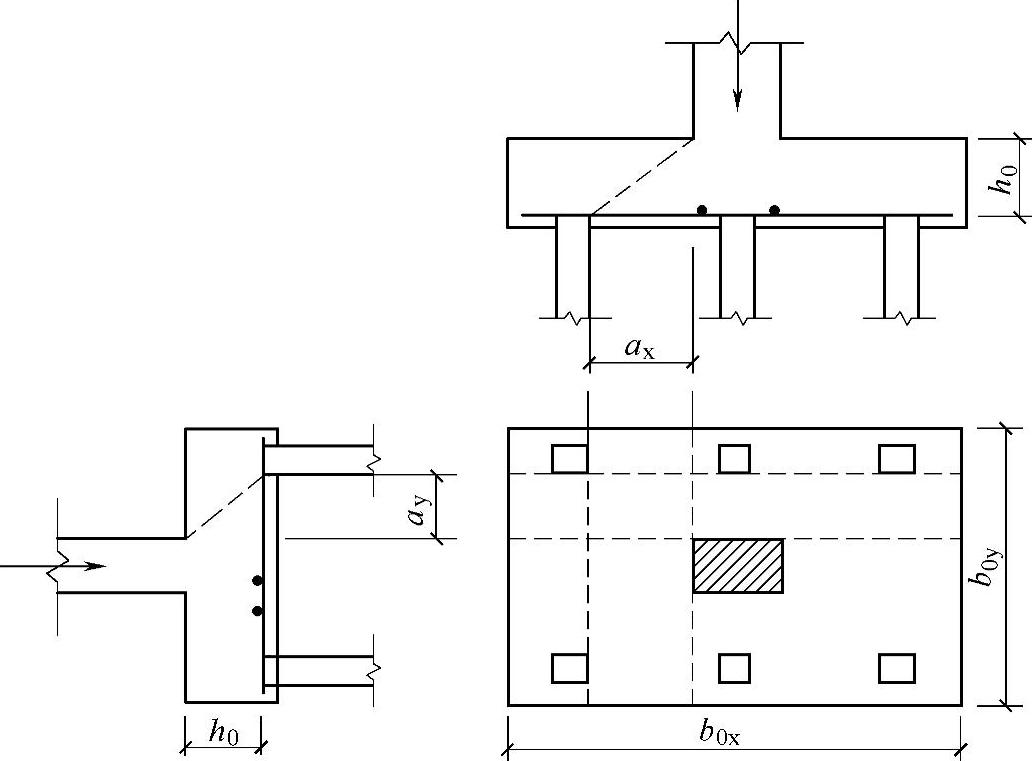
图5.9.10⁃1 承台斜截面受剪计算示意

式中 V——不计承台及其上土自重，在荷载效应基本组合下，斜截面的最大剪力设计值；

f_t——混凝土轴心抗拉强度设计值；

b₀——承台计算截面处的计算宽度；

h₀——承台计算截面处的有效高度；

α——承台剪切系数；按式（5.9.10⁃2）确定；

λ——计算截面的剪跨比，λ_x=a_x/h₀，λ_y=a_y/h₀，此处，a_x、a_y为柱边（墙边）或承台变阶处至y、x方向计算一排桩的桩边的水平距离，当λ<0.25时，取λ=0.25；当λ>3时，取λ=3；

β_hs——受剪切承载力截面高度影响系数：当h₀<800mm时，取h₀=800mm；当h₀>2000mm时，取h₀=2000mm；其间按线性内插法取值。

1.阶梯形承台的受剪计算

《建筑桩基技术规范》5.9.10条规定：

2 对于阶梯形承台应分别在变阶处（A₁—A₁，B₁—B₁）及柱边处（A₂—A₂，B₂—B₂）进行斜截面受剪承载力计算（图5.9.10⁃2）。

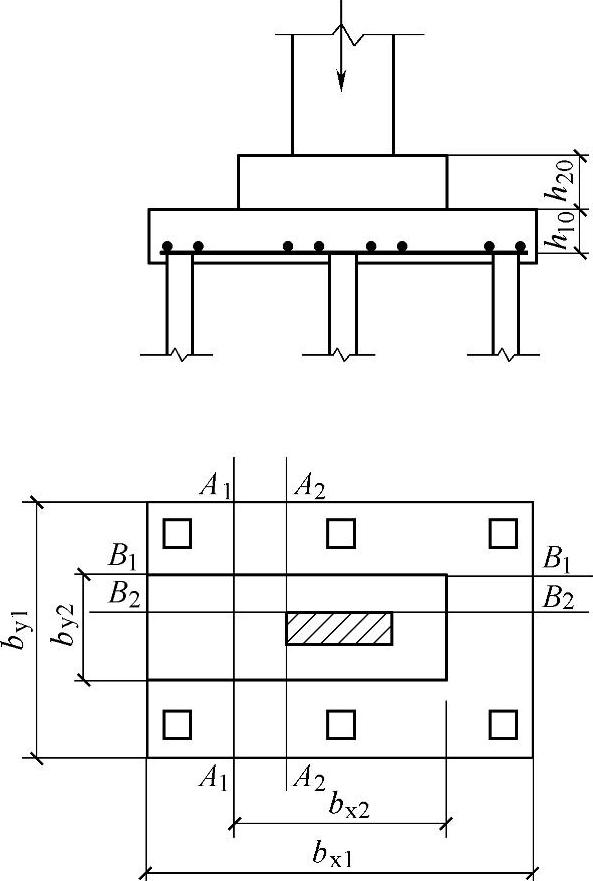
图5.9.10⁃2 阶梯形承台斜截面受剪计算示意

计算变阶处截面（A₁—A₁，B₁—B₁）的斜截面受剪承载力时，其截面有效高度均为h₁₀，截面计算宽度分别为b_y1和b_x1。

计算柱边截面（A₂—A₂，B₂—B₂）的斜截面受剪承载力时，其截面有效高度均为h₁₀+h₂₀，截面计算宽度分别为：

对A₂—A2

对B₂—B2

【9.1.21】 （2007年一级考题）

某框架结构柱基础，由上部结构传至该柱基的荷载标准值为：F=7600kN，M_x=M_y=800kN·m。柱基础独立承台下采用400mm×400mm钢筋混凝土预制桩，桩的平面布置及承台尺寸如图9.1.22所示。承台底面埋深3.0m，柱截面尺寸为700mm×700mm，居承台中心位置。承台采用C40混凝土，混凝土保护层厚度取50mm。承台及承台以上土的加权平均重度为20kN/m³。

试问，承台的斜截面抗剪承载力设计值（kN），与下列何项数值最为接近？

（A）5870 （B）6020 （C）6710 （D）7180

【答案】 （A）

【详解】 根据《建筑桩基技术规范》5.9.10条的规定，截面高度影响系数为

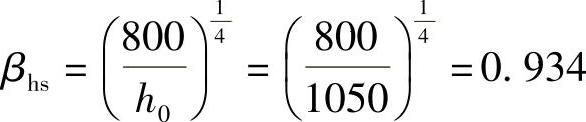
计算截面的剪跨比为

a_x=a_y=1050mm

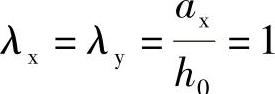
承台剪切系数为

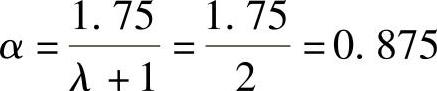
根据《建筑桩基技术规范》式（5.9.10⁃1），承台的斜截面抗剪承载力设计值为

β_hsαf_tb₀h₀=0.934×0.875×1.71×4000×1050=5871kN

故（A）正确。

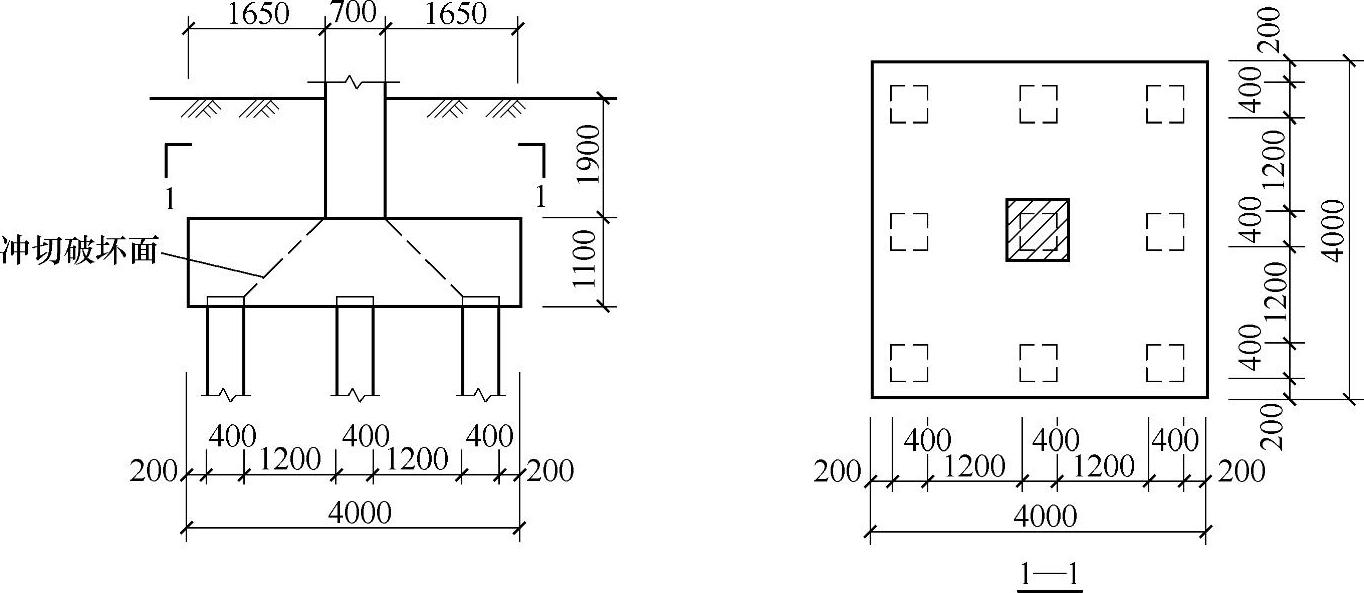
图 9.1.22

【简解】 所求为

β_hsαf_tb₀h₀=0.934×0.875×1.71×4000×1050=5871kN

其中

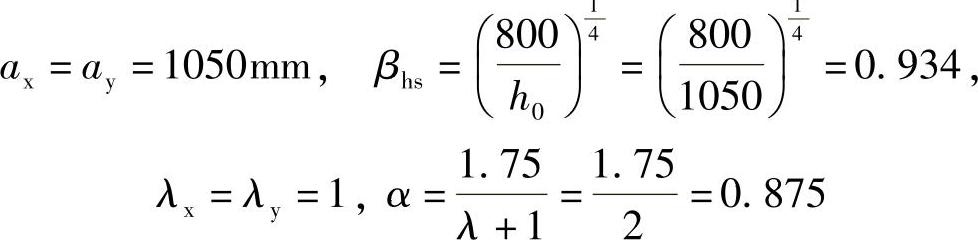
【9.1.22】 （2005年二级考题）

柱下钢筋混凝土承台，桩及承台相关尺寸如图9.1.23所示，柱为方柱，居承台中心。柱相应于荷载效应基本组合的轴力设计值N=9500kN；承台采用C40混凝土，混凝土保护层厚度取110mm。

试问，承台的斜截面抗剪承载力设计值（kN），与下列何项数值最为接近？

（A）5840 （B）6285 （C）7180 （D）7520

【答案】 （A）

【详解】 已知h₀=1040mm，f_t=1.71N/mm2

根据《建筑桩基技术规范》5.9.10条的规定，截面高度影响系数为

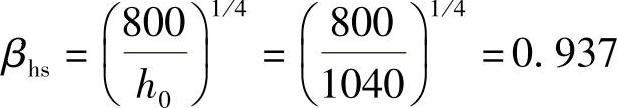
计算截面的剪跨比为

a_x=a_y=1050mm

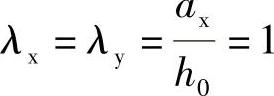
承台剪切系数为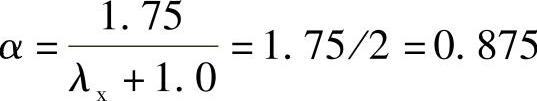

根据《建筑桩基技术规范》式（5.9.10⁃1），承台的斜截面抗剪承载力设计值为

β_hsαf_tb₀h₀=0.937×0.875×1.71×10³×4.0×1.04=5832kN

故（A）正确。

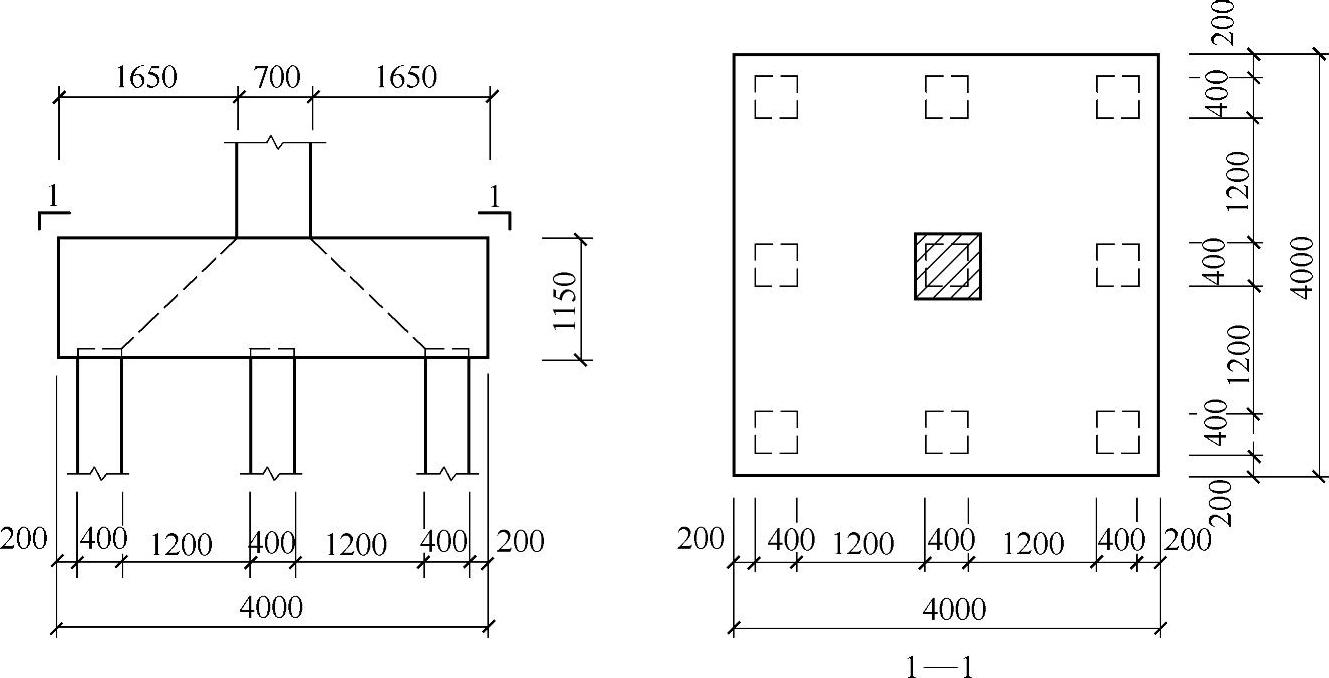
图 9.1.23

【简解】 所求为

β_hsαf_tb₀h₀=0.937×0.875×1.71×10³×4.0×1.04=5832kN

其中

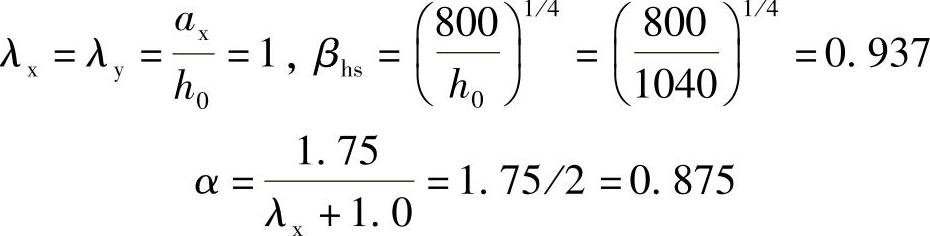
【9.1.23】 （2008年岩土考题）

如图9.1.24所示，竖向荷载设计值F=24000kN，承台混凝土为C40，按《建筑桩基技术规范》验算柱边A—A至桩边连线形成的斜截面的抗剪承载力与剪切力之比（抗力/V）最接近下列哪个选项？

（A）1.05 （B）1.2 （C）1.3 （D）1.4

【答案】 （A）

【解答】 （1）抗剪承载力

剪跨比λ_x=a_x/h₀=1.0/1.3=0.77

h=h₀+0.05=1.3+0.05=1.35m

当h=1.35m时，β_hs=0.886

b₀=4.2m

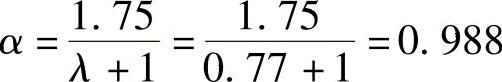
C40混凝土，f_t=1.71MPa

根据《建筑桩基技术规范》式（5.9.10⁃1），承台的斜截面抗剪承载力设计值为

β_hsαf_tb₀h₀=0.886×0.988×1.71×10³×4.2×1.3=8178kN

（2）剪切力为

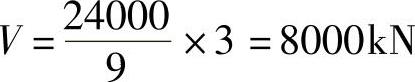
（3）抗剪承载力与剪切力之比为

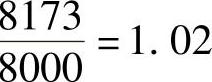
【9.1.24】 （2010年岩土考题）

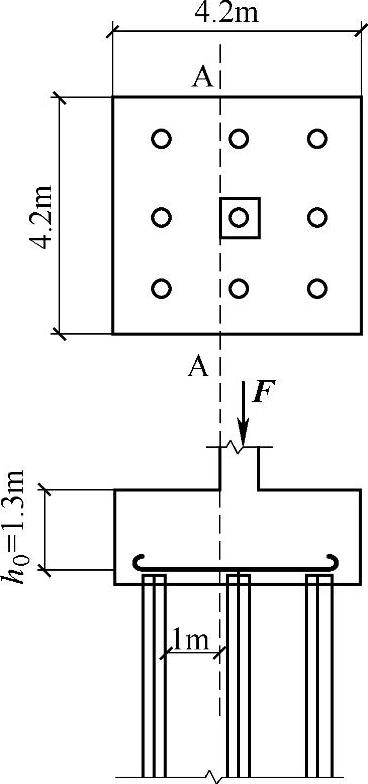
图 9.1.24

柱下桩基承台，如图9.1.25所示，承台混凝土轴心抗拉强度设计值f_t=1.71MPa，试按《建筑桩基技术规范》，计算承台柱边A₁—A₁斜截面的受剪承载力，其值与下列何项数值最为接近？（图中尺寸以mm计）

（A）1.00MN （B）1.21MN （C）1.35MN

【答案】 （A）

【解答】A₁—A₁截面处有效高度h₀=300+300=600mm=0.6m对此截面，计算宽度b₀=1500mm

h₀<800mm，取h₀=800mm，则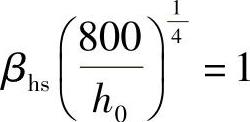

剪跨比λ=a/h₀=1000/600=1.667，则承台剪切系数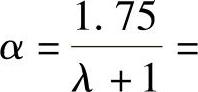

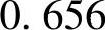
根据《建筑桩基技术规范》式（5.9.10⁃1），承台的斜截面抗剪承载力设计值为

V≤β_hsαf_tb₀h₀

V≤1.0×0.656×1.71×1.5×0.6=1.01MN

2.锥形承台的受剪计算

《建筑桩基技术规范》规定：

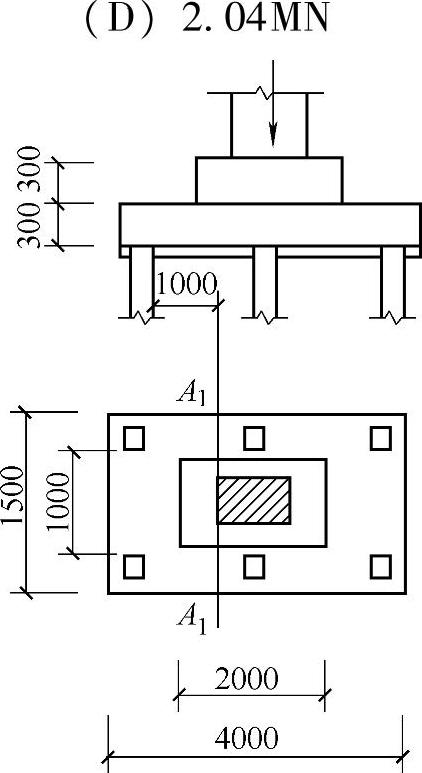
图 9.1.25

3 对于锥形承台应对变阶处及柱边处（A—A及B—B）两个截面进行受剪承载力计算（见图5.9.10⁃3），截面有效高度均为h₀，截面的计算宽度分别为：对A—A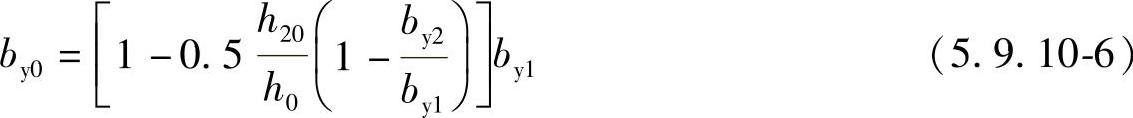

对B—B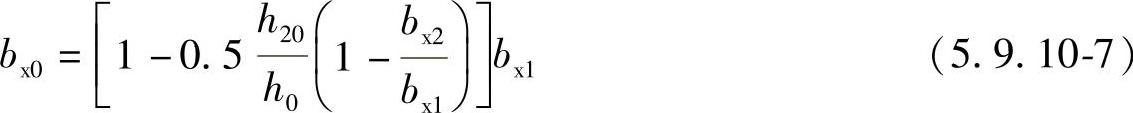

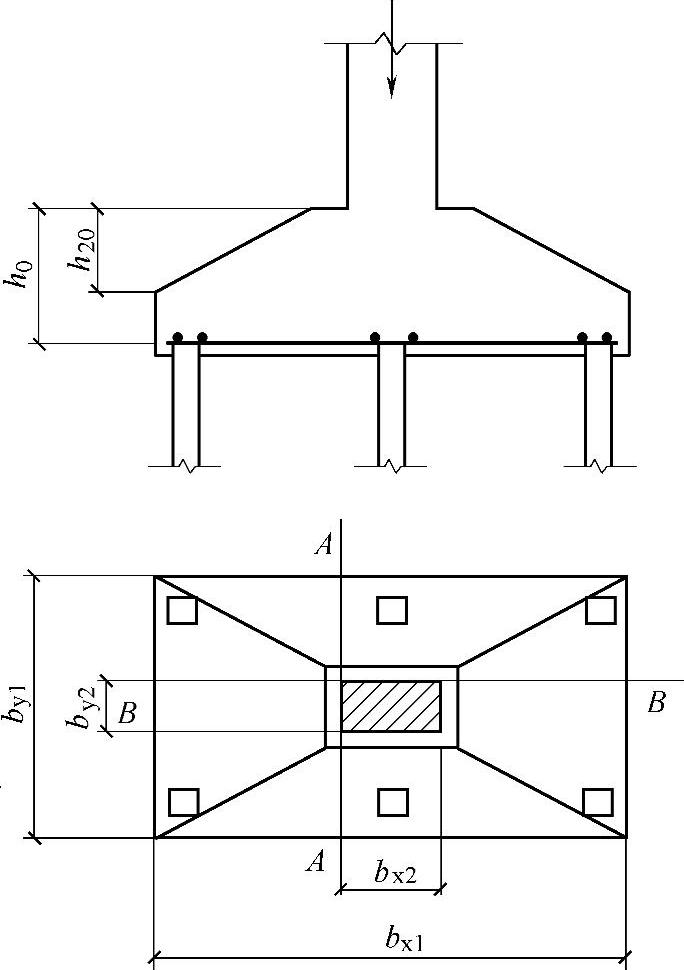
图5.9.10⁃3 锥形承台斜截面受剪计算示意

【9.1.25】 （2003年二级考题，原题是连锁题的子题，情境描述有所简化）

某柱下桩基础采用6根沉管灌注桩，桩身设计直径d=388mm，如图9.1.26所示。作用于承台顶面的外力有相应于荷载效应标准组合时的竖向力F_k、力矩M_k、水平力H_k。柱截面尺寸为350mm×400mm。

假定F_k=1953kN，已知承台自重及其以上土的自重标准值G_k=3240kN。当按承载能力极限状态下永久荷载效应控制的基本组合（采用简化规则）计算承台内力时，承台斜截面的最大剪力设计值V_max与下列何项数值最为接近？

（A）1464.77kN （B）1318.29kN （C）976.51kN （D）878.86kN

【答案】 （B）

【详解】 根据《建筑桩基技术规范》5.9.10条的规定，扣除G_k值后相应于荷载效应基本组合时的单桩竖向力设计值为

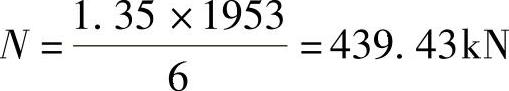
所以V_max=439.43×3=1318.29kN

另一个方向两根桩V=439.43×2=878.86kN，比较可知最大剪力为1318.29kN。

故（B）正确。

【简解】

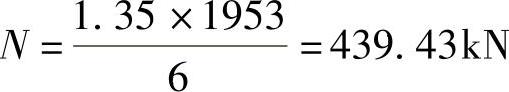
所以V_max=439.43×3=1318.29kN（另一个方向两根桩V=439.43×2=878.86kN）

图 9.1.26

【9.1.26】～【9.1.27】 （2012年一级考题）

某抗震设防烈度为8度（0.30g）的框架结构，采用摩擦型长螺旋钻孔灌注桩基础，初步确定某中柱采用如图9.1.27所示的四桩承台基础，已知桩身直径为400mm，单桩竖向抗压承载力特征值R_a=700kN，承台混凝土强度等级C30（f_t=1.43N/mm²），桩间距有待进一步复核。考虑x向地震作用，相应于荷载效应标准组合时，作用于承台底面标高处的竖向力F_Ek=3341kN，弯矩M_Ek=920kN·m，水平力V_Ek=320kN，承台有效高度h₀=730mm，承台及其上土重可忽略不计。

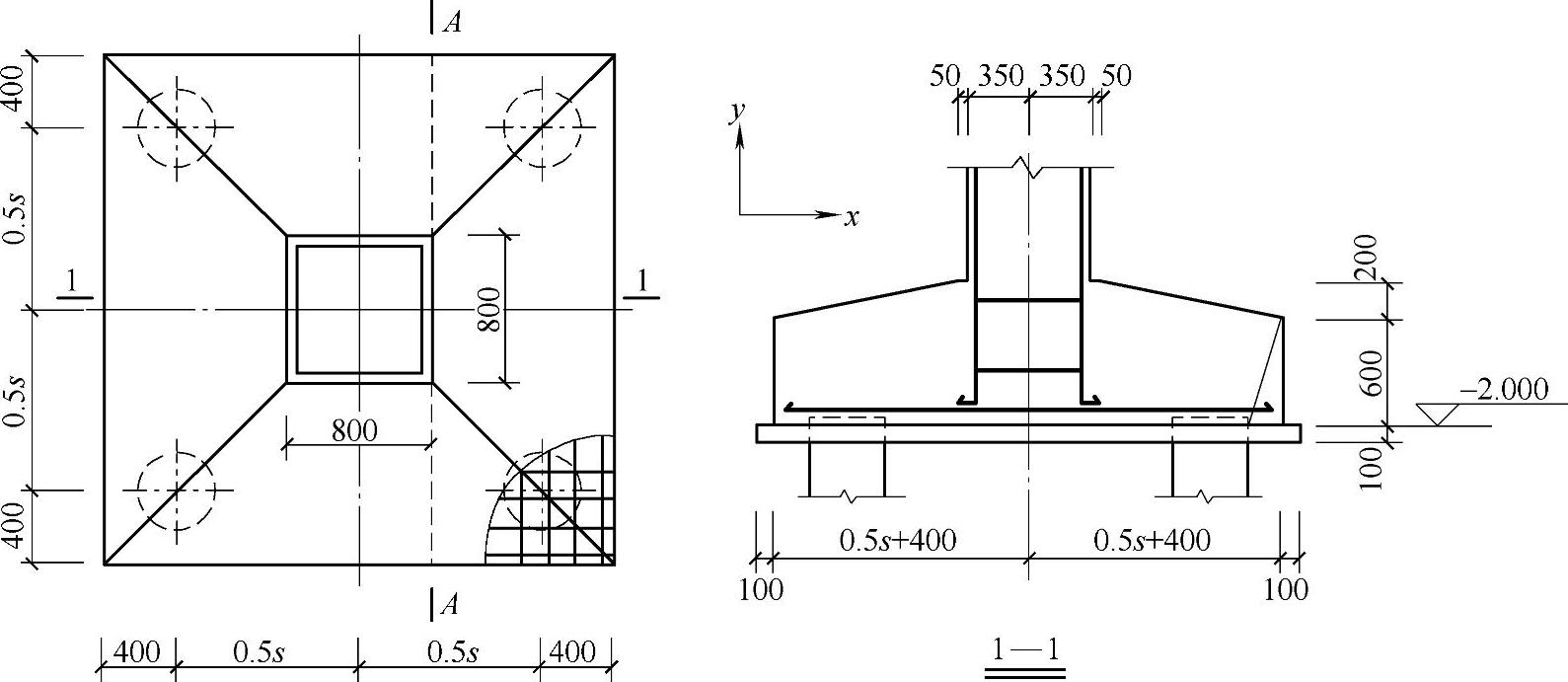
图 9.1.27

【9.1.26】 （2012年一级考题）

假定x向地震作用效应控制桩中心距，x、y向桩中心距相同，且不考虑y向弯矩的影响。试问，根据桩基抗震要求确定的桩中心距s（mm）与下列何项数值最为接近？

（A）1400 （B）1800 （C）2200 （D）2600

【答案】 （C）

【解答】 根据《建筑桩基技术规范》5.2.1条2款及式（5.2.1⁃4）：

N_Ekmax≤1.5R 1.5R=1.5×700=1050kN

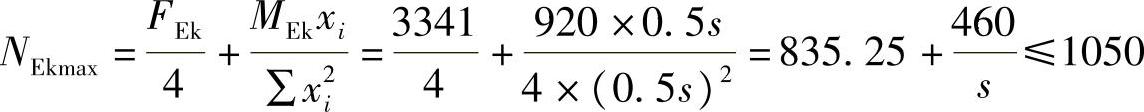
s≥2.142m，故应选2200mm。

【9.1.27】 （2012年一级考题）

试问，当桩中心距s=2400mm，地震作用效应组合时，承台A—A剖面处的抗剪承载力设计值（kN）与下列何项数值最为接近？

（A）3500 （B）3100 （C）2800 （D）2400

【答案】 （B）

【解答】 根据《建筑桩基技术规范》5.9.10，对锥形承台，有效高度h₀=730mm，有效宽度为

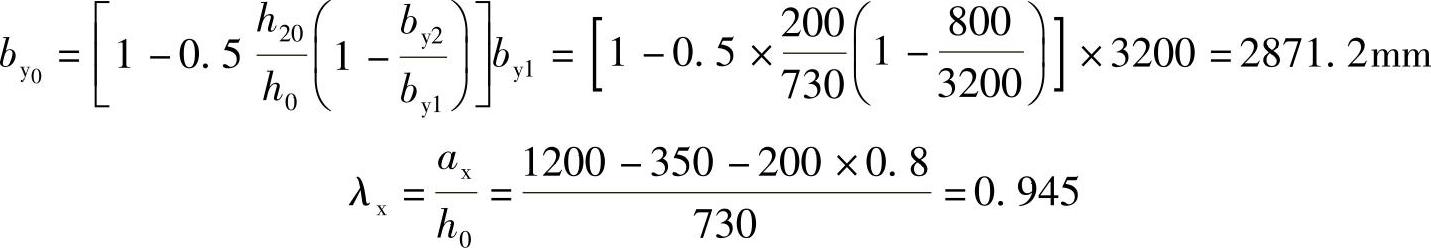
（注：上式中0.8为圆桩截面换算为方桩截面的换算系数）

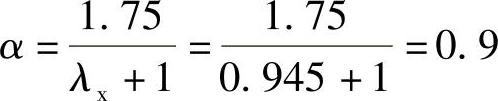
C30混凝土，f_t=1.43N/mm²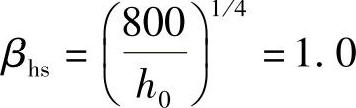，（当h₀<800mm时，取h₀=800mm）

根据《建筑桩基技术规范》表5.4.2，进行抗震验算时，抗剪承载力调整系数γ_RE=0.85

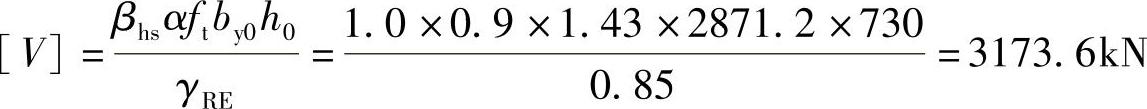
【9.1.28】 （2014年一级考题，原题为连锁题中一道子题）

某地基基础设计为乙级的柱下桩基础，承台下布置有5根边长为400mm的C60钢筋混凝土预制方桩，框架柱截面尺寸为600mm×800mm，承台及其以上土的加权平均重度γ=20kN/m³，承台平面尺寸、桩位布置等如图9.1.28所示。

假定，承台混凝土强度等级为C30（f_t=1.43N/mm²），承台计算截面的有效高度h₀=1500mm。试问，图中柱边A—A截面承台的斜截面承载力设计值（kN），与下列何项数值最为接近？

（A）3700 （B）4000 （C）4600 （D）5000

【答案】 （A）

【解答】 （1）计算截面的剪跨比

根据《建筑桩基技术规范》5.9.10条：

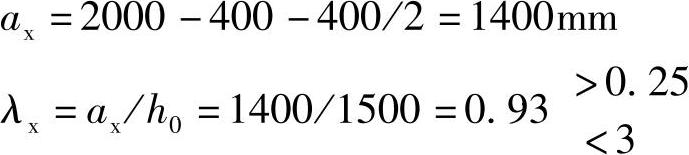
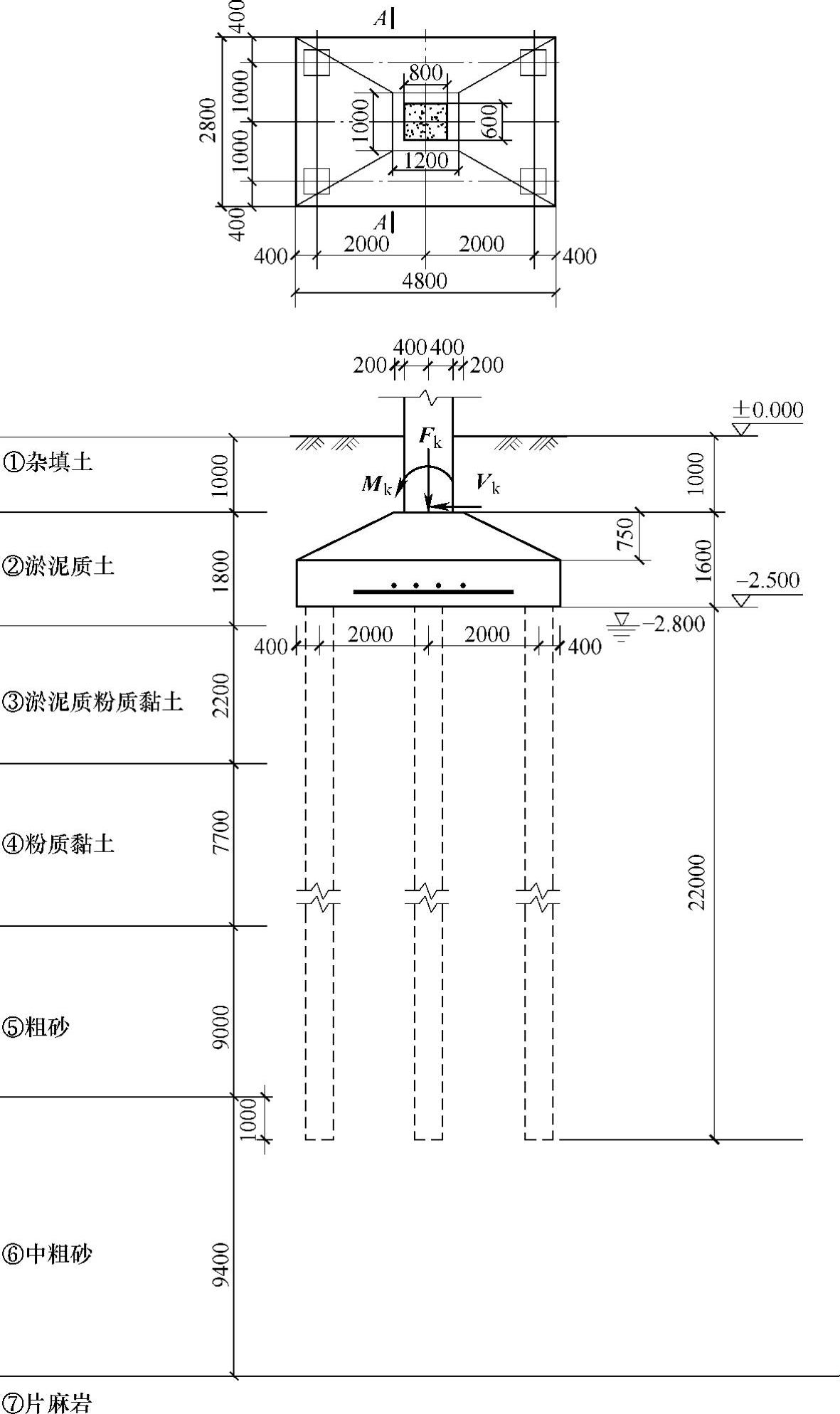
图 9.1.28

（2）求锥形承台A—A截面的计算宽度b_y0

根据《建筑桩基技术规范》5.9.10条3款：

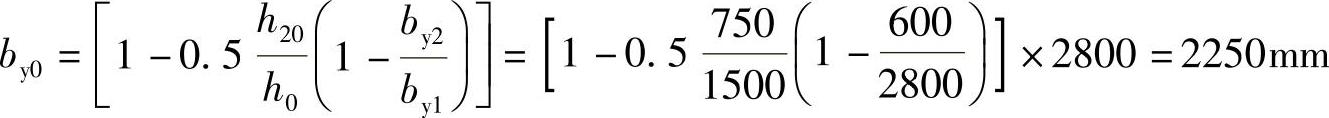
（3）求承台剪切系数

根据《建筑桩基技术规范》式（5.9.10⁃2）：

α=1.75/（λ+1）=1.75/（0.93+1）=0.907

（4）求柱边A—A截面承台的斜截面承载力设计值

f_t=1.43，根据《建筑桩基技术规范》式（5.9.10⁃1）：

V=β_hsαf_tb₀h₀=0.855×0.907×1.43×2250×1500=3743kN

故选（A）。

（四）局部受压计算

当承台的混凝土强度等级比柱子或桩的强度等级低时，《建筑桩基技术规范》5.9.15条规定要进行承台的局部受压验算。具体计算公式见《混凝土结构设计规范》。

5.9.15 对柱下桩基，当承台的混凝土强度等级低于柱或桩的混凝土强度等级时，应验算柱下或桩上承台的局部受压承载力。

【9.1.29】 承台局部受压承载力验算

条件：某桩基承台如图9.1.29所示，柱截面尺寸为400mm×600mm，柱的混凝土强度等级为C30，承台混凝土强度等级为C20。作用在基础顶面的荷载设计值为：F=2200kN。

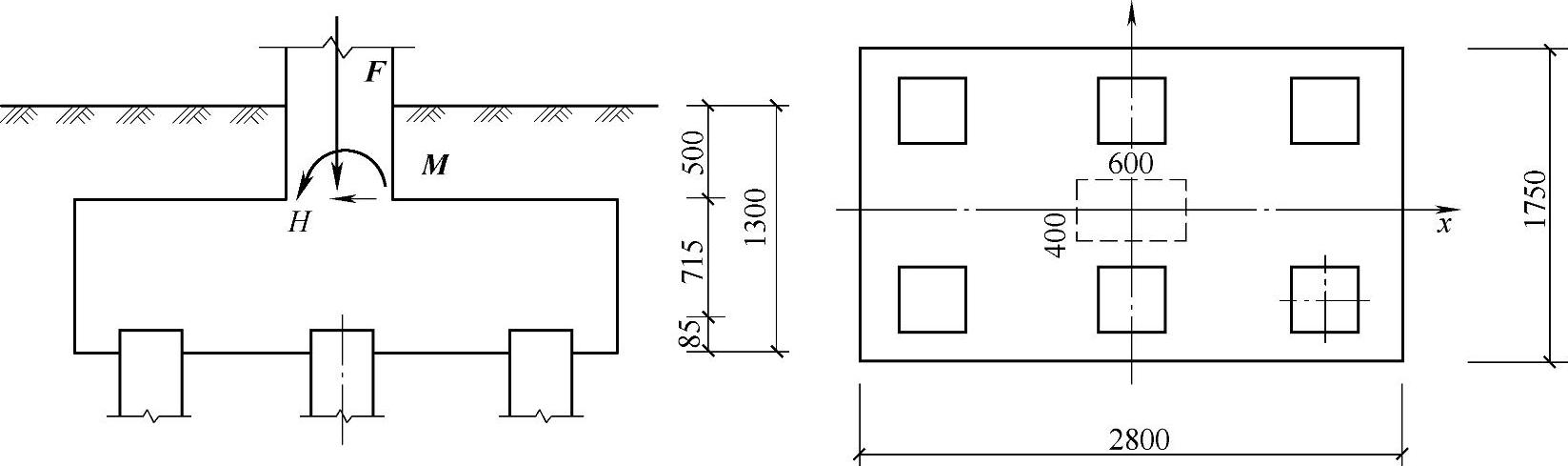
图 9.1.29

要求：验算承台在柱下的局部受压承载力。

【解答】 由于承台混凝土强度等级低于柱的混凝土强度等级，需按《混凝土结构设计规范》验算承台在柱下局部受压承载力。C20混凝土，f_c=9.6kPa；f_cc=0.85f_c=8.16kPa。

柱子截面边长为400mm×600mm，柱混凝土强度等级C30，承台局部受压面积

A_l=0.4×0.6=0.24m²

局部受压的计算底面积

A_b=（3×0.4）×（2×0.4+0.6）=1.68m²

混凝土局部受压时的强度提高系数

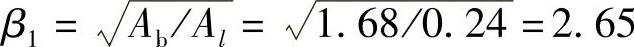
荷载的分布影响系数ω=1.0。

根据《混凝土结构设计规范》式（D.5.1⁃1）得局部抗压承载力

ωβ₁f_ccA_l=1.0×2.65×8.16×0.24×10⁶=5190kN>F=2200kN，满足要求。