1.可压缩土层为一层
如图5.2.1所示覆盖面很大的单一压缩土层,荷载的分布面积亦很大。设在压力p1作用下土样的高度为H,孔隙比e1。当压力从p1增加到p2时,产生的压缩量Δs并稳定后,孔隙比从e1减少到e2。由于土在受压过程中不能侧向变形,根据受压前土粒体积和土样横截面积均不改变的条件,可得单一土层单向压缩变形

上式即为侧限条件下计算土的压缩量的基本公式,根据上述压缩系数和压缩模量之间的关系式,还可导出如下公式
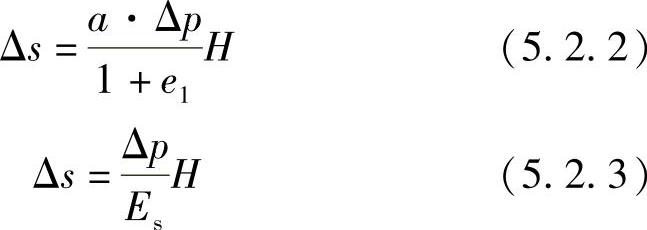
根据以上公式,就可计算土的压缩变形量。
 【5.2.1】 (2007年岩土考题)
【5.2.1】 (2007年岩土考题)

图 5.2.1
某条形基础持力层下面有厚度2.0m的正常固结黏土层,已知黏土层中部的自重压力为50kPa,附加压力为100kPa,此土层取土做固结试验结果见表5.2.1,试计算该土层的压缩变形量。
表 5.2.1

【解答】 黏土层中部自重压力加附加压力为50+100=150kPa,p=150kPa,对应的孔隙比e=0.95。
压缩系数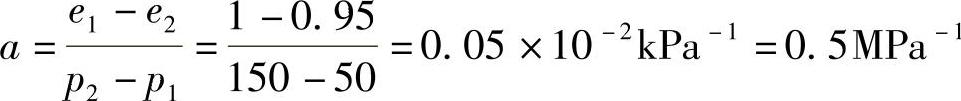
压缩模量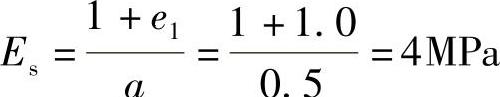
黏土层压缩变形量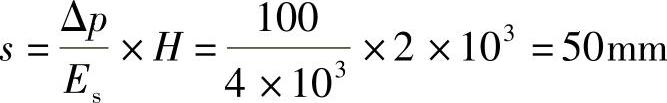
【5.2.2】 单层土的最终沉降量计算
条件:某基础长4.8m,宽3m,基底平均压力标准值p=170kPa,基础底面标高处的土自重应力σcd=20kPa,地基为均质黏土层,厚度1.2m,孔隙比e1=0.8,压缩系数a=0.25MPa-1,黏土层下为不可压缩的岩层。
要求:试计算基础的最终沉降量。
【解答】 (1)计算基底附加压力p0
p=170kPa,σcd=20kPa
p0=p-σcd=170-20=150kPa
(2)求压缩模量Es
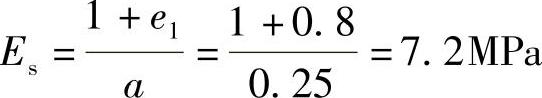
(3)求基础的最终沉降量
该基础下的地基情况是:1.2m厚的黏土层以下为不可压缩岩层,故沉降计算至岩层的上表面为止。
由公式
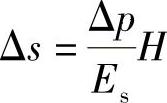
可知该土层的变形量为: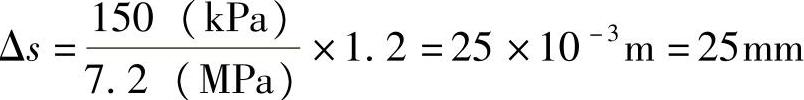
2.可压缩土层为多层
当可压缩土层为多层而需计算其中第i土层的压缩变形量Δsi时,仍采用式(5.2.2)计算,此时取Δs=Δsi、H=hi。
式中 Δp——薄压缩土层顶面和底面的附加应力平均值,kPa;
e1i——第i层土的自重应力平均值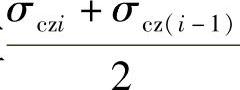 (即p1i)对应的压缩曲线上的孔隙比;
(即p1i)对应的压缩曲线上的孔隙比;
σczi、σcz(i-1)——第i层土底面、顶面处的自重应力,kPa;
e2i——第i层自重应力平均值与附加应力平均值之和对应的压缩曲线上的孔隙比;
hi——第i层土的厚度,m。
【5.2.3】 单层土的压缩变形量计算
条件:某土层厚5m,原自重压力p1=100kPa。现在考虑在该土层上建造建筑物,估计会增加压力Δp=150kPa。取土作压缩试验结果见表5.2.2。
表 5.2.2(https://www.xing528.com)

要求:求该土层的压缩变形量为多少?
【解答】 已知:p1=100kPa,Δp=150kPa,h=5m
所以,p2=p1+Δp=100+150=250kPa
由压缩试验结果可得:e1=1.12 e2=0.95(p2=250kPa,用上表结果插入求得)
则该厚度为5m的土层的压缩变形量为:
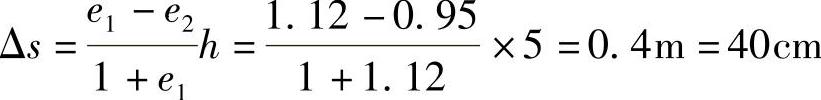
或用另一法求: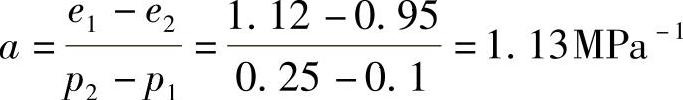
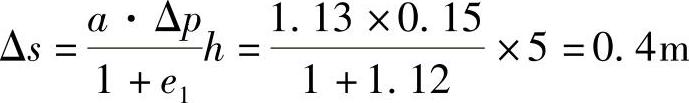
由a=1.13MPa-1知此为高压缩性土,所以变形量很大。
【5.2.4】 计算土层压缩量
条件:矩形基础底面尺寸b×l=3m×3m,自重应力和附加应力分布图如图5.2.2a所示,第二层土的压缩曲线如图5.2.2b所示。
要求:计算第二层土的压缩量。
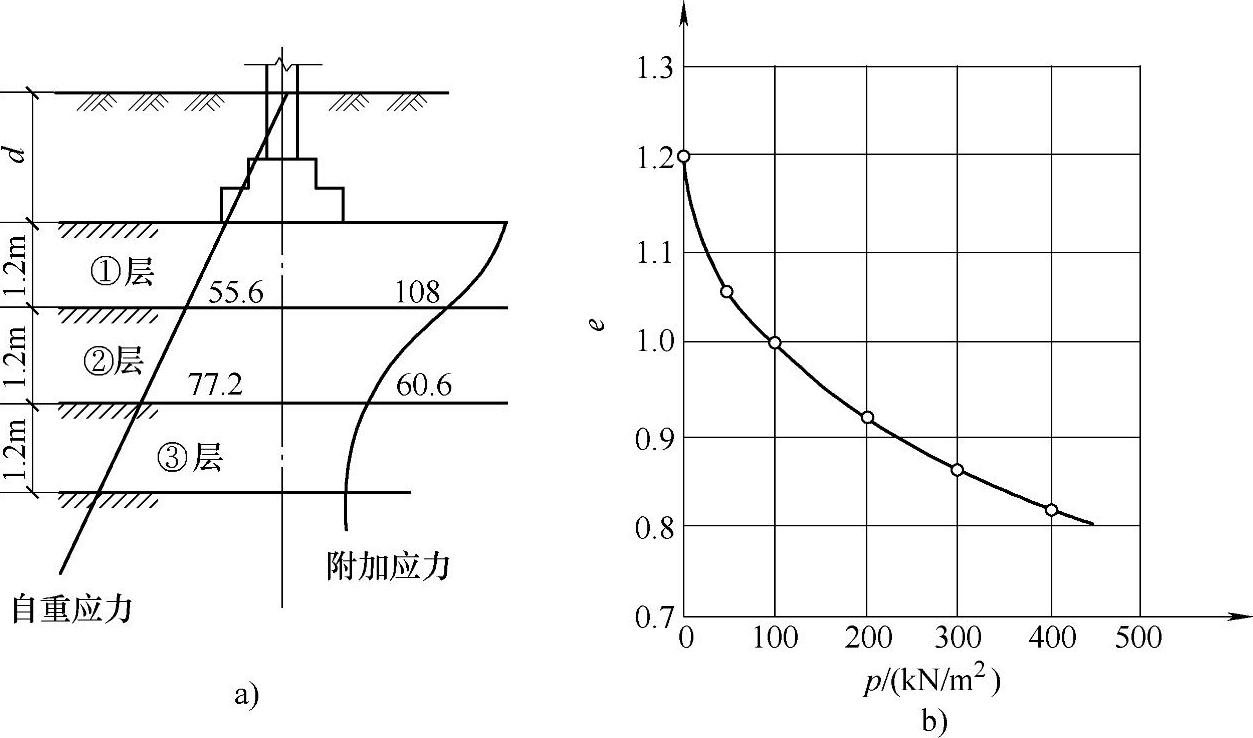
图 5.2.2
【解答】 (1)计算第二层土的平均自重应力
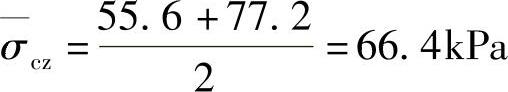
(2)计算第二层土平均附加应力
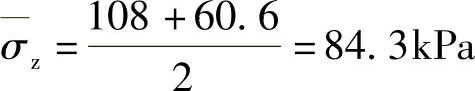
(3)求p1和p2
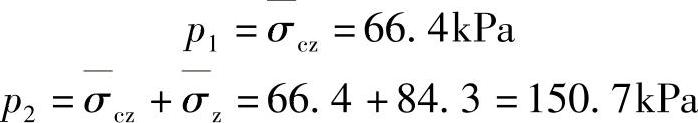
(4)求e1和e2
由图5.2.2b压缩曲线可查得相应于p1和p2的孔隙比
e1=1.030,e2=0.95
(5)计算第二层土的压缩量
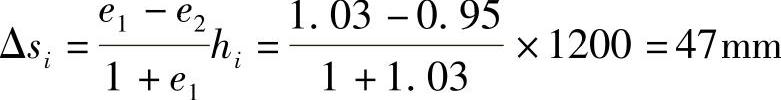
 【5.2.5】 (2009年岩土考题)
【5.2.5】 (2009年岩土考题)
某建筑物长度50m,宽度10m,比较筏板基础和1.5m的条形基础两种方案。已分别求得筏板基础和条形基础中轴线上变形计算深度范围内(为简化计算,假定两种基础的变形计算深度相同)的附加应力随深度分布的曲线(近似为折线)如图5.2.3所示。已知持力层的压缩模量Es=4MPa,下卧层的压缩模量Es=2MPa。估算由于这两层土的压缩变形引起的筏板基础沉降sf与条形基础沉降st之比最接近于下列何项数值?
(A)1.23 (B)1.41 (C)1.65 (D)1.86
【答案】 (A)
【解答】 由沉降量的计算公式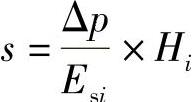 ,筏板基础的沉降量为
,筏板基础的沉降量为
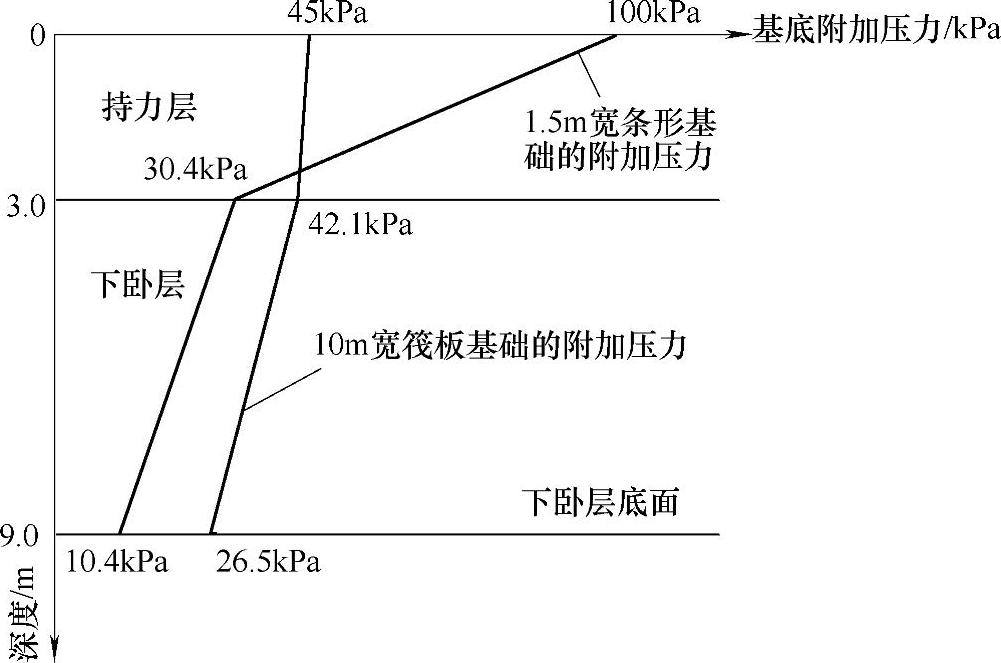
图 5.2.3
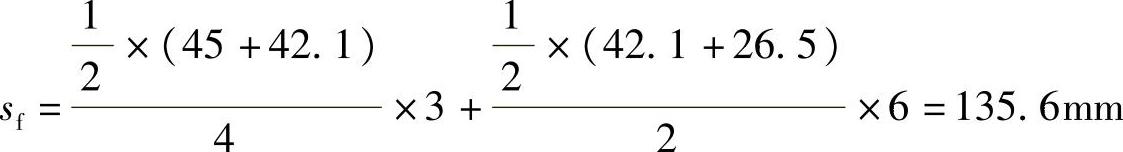
条形基础的沉降量为
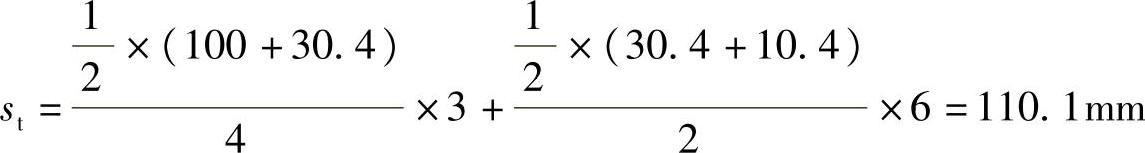
筏板基础的沉降量与条形基础的沉降量之比为
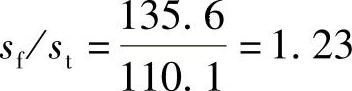
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




