用角点法计算土中附加应力

土中附加应力是由建筑物荷载在地基内引起的应力，通过土粒之间的传递，向水平与深度方向扩散，并逐渐减小，如图3.4.1所示，假设将构成地基土的土粒看做是无数个直径相同的小圆柱，当沿垂直纸面方向作用一个线荷载F=1，左图表示各深度处水平面上各点垂直应力大小，右图为集中力下各深度处的垂直应力大小。我们从该图可以形象地看到土中附加应力分布的特点。

（1）在地面下同一深度的水平面上各点的附加应力不等，沿力的作用线上的附加应力最大，向两边逐渐减小。

（2）距地面越深，附加应力分布范围越大，在同一铅直线上的附加应力不同，距地面越深，其值越小。

可见，地基中附加应力离荷载作用点越远，其值越小。我们称这种现象为附加应力的扩散作用。

图3.4.1 地基中附加应力扩散示意图

土中附加应力的计算方法有两种：一种是弹性理论方法；另一种是应力扩散角方法。后者在下一段中叙述。前者是假定地基为半无限均质弹性体，用弹性力学公式求解。现简述一种中心受压矩形基础作用下的“角点法”于下。

利用角点应力表达式，可以求算平面上任意点M（可以在矩形面积之外）下任意深度处的竖向应力，这种方法称为角点法。《建筑地基基础设计规范》附录K就是采用这种方法。

角点法求任意点应力的做法，是通过点M做一些辅助线，使M成为几个矩形的公共角点，M点以下z深度的应力σ_z就等于这几个矩形在该深度引起的应力之总和。根据M点位置不同，可分下列几种情况：

（1）M点在矩形均布荷载面以内时（图3.4.2a）：

σ_z（M）=（α_Ⅰ+α_Ⅱ+α_Ⅲ+α_Ⅳ）p

式中 p——基础底面的平均附加压力（kPa）；

α_Ⅰ、α_Ⅱ、α_Ⅲ、α_Ⅳ——小矩形Ⅰ、Ⅱ、Ⅲ、Ⅳ的角点附加应力系数，分别根据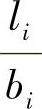、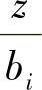（l_i、b_i—每个小矩形的长边和矩边）查《建筑地基基础设计规范》附录K表K.0.1⁃1。

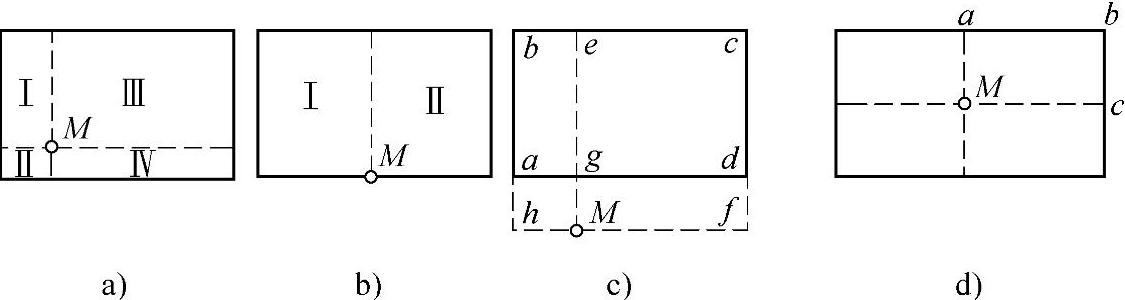
图3.4.2 按角点法确定地基应力

对图3.4.2b的情况有

σ_z（M）=（α_Ⅰ+α_Ⅱ）p

（2）M点在矩形均布荷载面以外时（图3.4.2c）：

σ_z（M）=[α_（Mb）+α_（Mc）-α_（Ma）-α_（Md）]p

式中 α_（）——表示矩形Mhbe、Mecf、Mhag、Mgdf的角点附加应力系数，查表K.0.1⁃1可得。

（3）M点在矩形均布荷载面的中点时，这时只需将荷载面划成四等分（图3.4.2d），M点下的σ_z值只是小矩形Mabc的4倍而已。

《建筑地基基础设计规范》规定：

附录K 附加应力系数α、平均附加应力系数α

K.0.1 矩形面积上均布荷载作用下角点的附加应力系数α、平均附加应力系数α（表K.0.1）。

表K.0.1⁃1 矩形面积上均布荷载作用下角点附加应力系数α

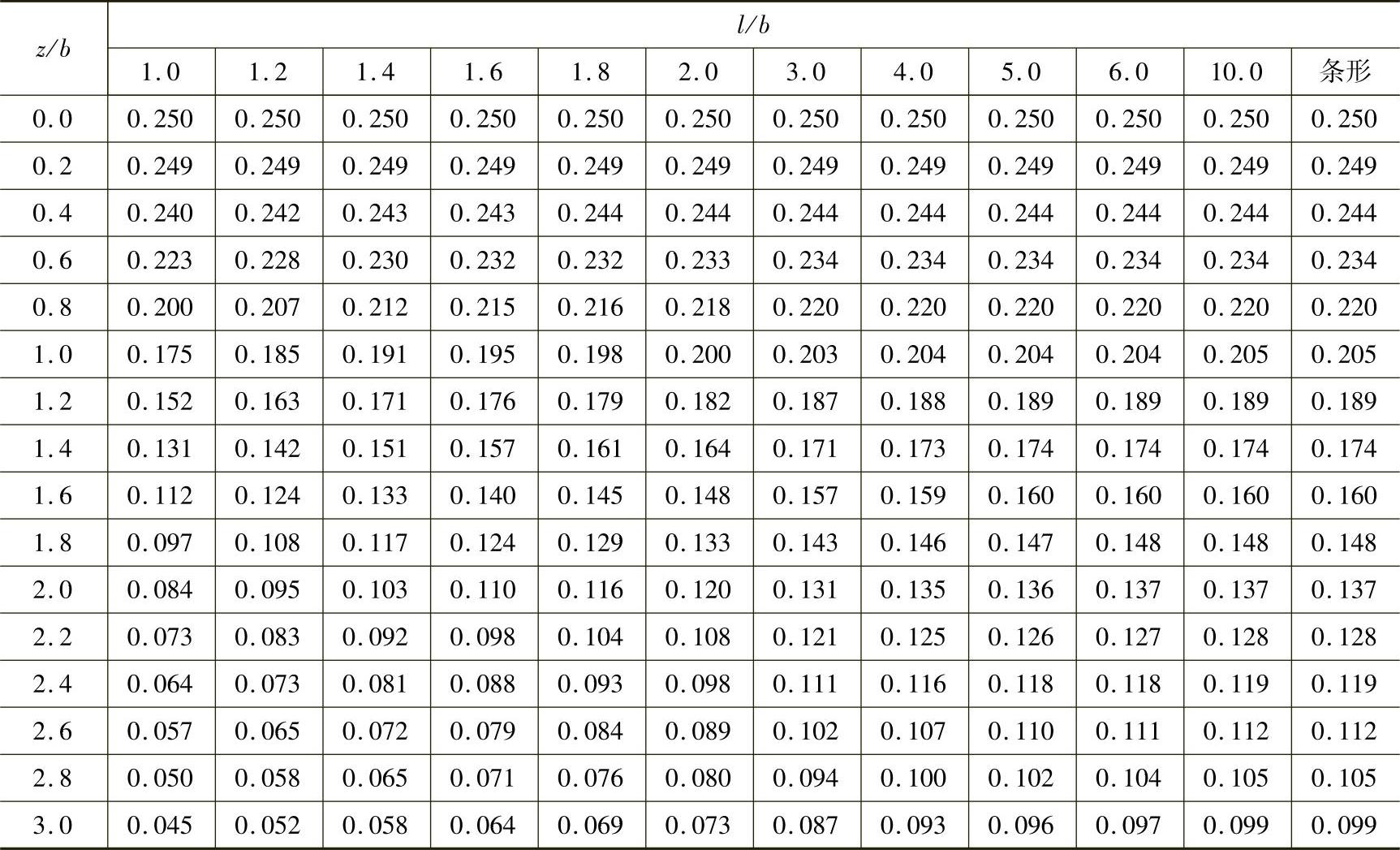
注：l—基础长度（m）；b—基础宽度（m）；z—计算点离基础底面垂直距离（m）。

【3.4.1】 基础中心点下的垂直附加应力条件：已知建筑物单柱基础面积为4m×6m，基底附加压力p₀=30kPa。要求：基础中心点下深度z=2m处的垂直附加应力σ_z。

【解答】

查《建筑地基基础设计规范》附录K得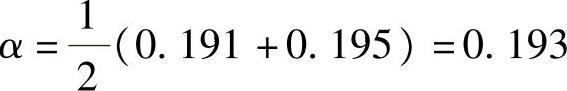

σ_z=4αp₀=4×0.193×30=23.16kPa

【3.4.2】 用角点法求基础平面中点基底下的附加应力

条件：基础底面埋深D=1.5m，基础尺寸B×L=1.25m×2m，地面处由上部结构传来荷载200kN，基底上下均为黏土，土的重度γ=18.1kN/m³，饱和重度为19.7kN/m³，地下水位位于基底下1.0m处。

图 3.4.3

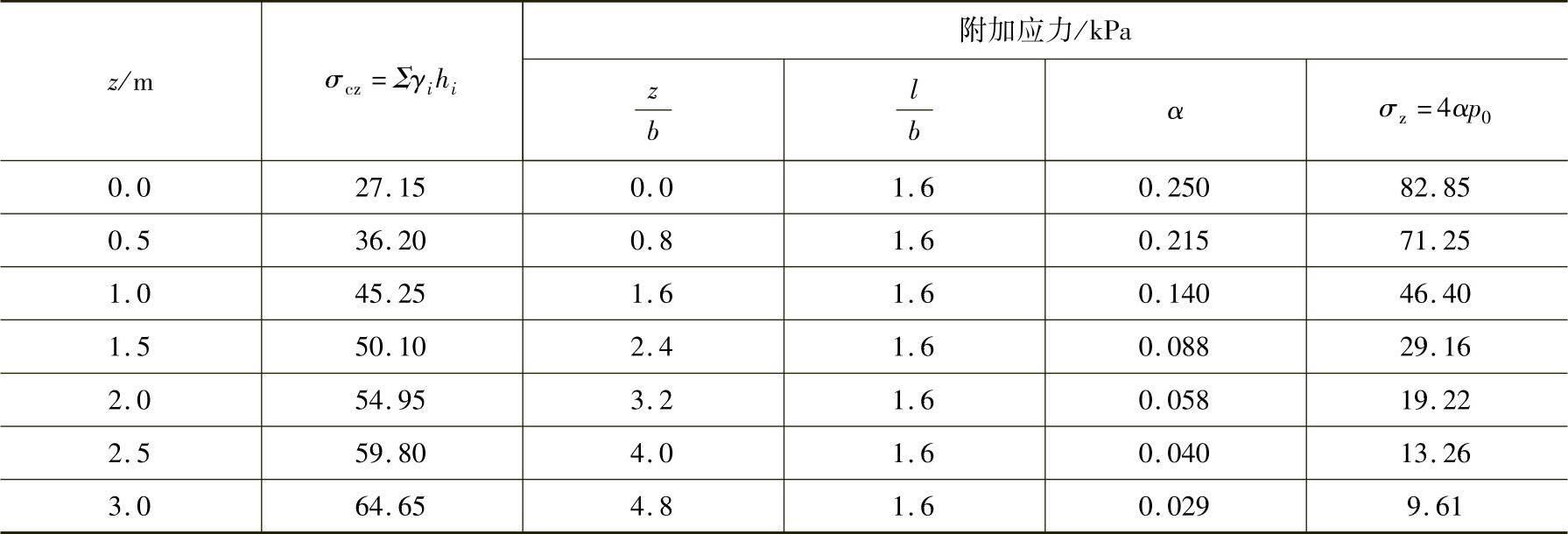
要求：如图3.4.3所示基底下1.0m、1.5m、2.0m、2.5m、3.0m处的自重应力和附加应力，并绘出其曲线。

【解答】 （1）地基中的自重应力基础底面：

σ_cz=γd=18.1×1.5=27.15kPa

地下水位面：

σ_cz=27.15+18.1×1.0=45.25kPa

地面下4.5m处：

σ_cz=45.25+（19.7-10）×2.0=64.65kPa

（2）基底附加压力

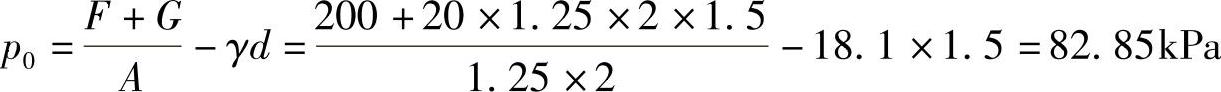
基底以下各点附加应力用角点法l=1m，b=0.625m，自重应力和附加应力计算见表3.4.1，曲线如图3.4.3所示。

表3.4.1 自重应力和附加应力计算表

【3.4.3】 （2007年二级考题）

某柱下独立基础地面尺寸为4.8m×2.4m，埋深1.5m，如图3.4.4所示。土层分布自地表起依次为：黏土，厚度2.5m；粉质黏土，厚度2m；黏土，厚度4.5m。地下水位在地表下1.5m处。基础及基底以上填土的加权平均重度为20kN/m³。

假定矩形面积上均布荷载作用下角点的附加应力系数见表3.4.2。试问，当基底的附加压力为202.7kPa时，在基底中心点下7.5m处土的附加应力（kPa），与下列何项数值最为接近？

（A）37.46 （B）22.9 （C）10.9 （D）5.45

【答案】 （B）

【详解】 作题提示：计算附加应力时，最后求附加应力使用的附加应力系数是划分的各个小矩形附加应力系数之和，例如计算基底中心点处的附加应力，最后求附加应力时应乘以4。

过基础中心点划分为面积相等的四个小矩形，每个小矩形的短边为b=1.2m，长边为l=2.4m，计算点在基底中心点下的深度为z=7.5m。

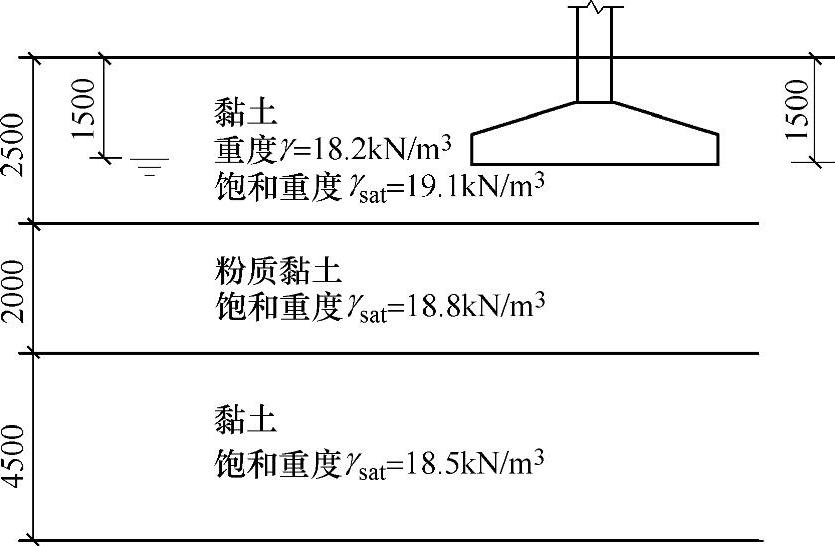
图 3.4.4

表 3.4.2

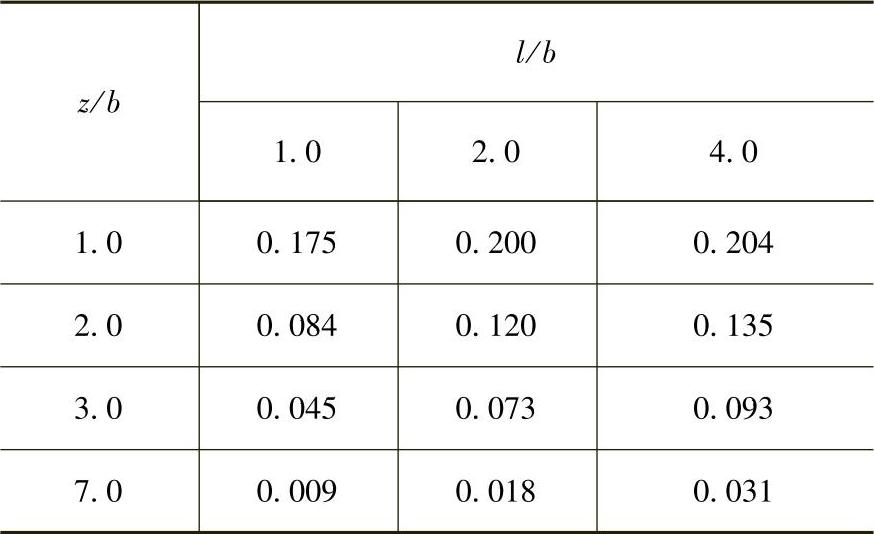
查询附加应力系数时，用到的比值如下

l/b=2.0，z/b=7.5/1.2=6.25

查询表3.4.2，并线性插值，得一个小矩形的附加应力系数为

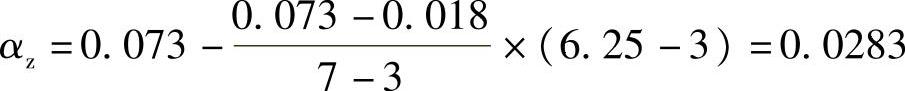
在基底中心点下7.5m处土的附加应力为(www.xing528.com)

σ_z=4αp₀=4×0.0283×202.7=22.9kPa

故（B）正确。

【简解】 划分为四个小矩形，则

l/b=2.0，z/b=6.25

查得α_z=0.0283

σ_z=4αp₀=4×0.0283×202.7=22.9kPa

【3.4.4】 （2007年岩土考题）

条件：某高低层一体的办公楼，采用整体筏形基础（图3.4.5），基础埋深7.0m，高层部分基础尺寸为40m×40m，基底压力430kPa，多层部分基础尺寸40m×16m，土层重度γ=20kN/m³，地下水位埋深3.0m。

要求：试求高层部分的荷载在多层建筑基底中心点以下深度12m处所引起的附加压力。

【解答】 高层基底附加压力为

图 3.4.5

p₀=p_k-γh=430-（3×20+4×10）=330kPa

面积acoel/b=48/20=2.4，z/b=12/20=0.6

α₁=0.2334

面积bcodl/b=20/8=2.5，z/b=12/8=1.5，α₂=0.16

p=p₀（2α₁-2α₂）=330×（2×0.2334-2×0.16）=48.4kPa

【3.4.5】 不同长度基础的附加应力

条件：三个宽度相同，长度不同的基础，它们的基底尺寸分别为2m×2m、4m×2m、20m×2m，埋深都是1m，地基土重度为18N/m³。作用在基底面上的中心荷载（F+G）分别为472kN、944kN、236kN。

要求：试求这三个基础中心点下z=2m处的竖向附加应力。

【解答】 （1）基础1：l=b=2m

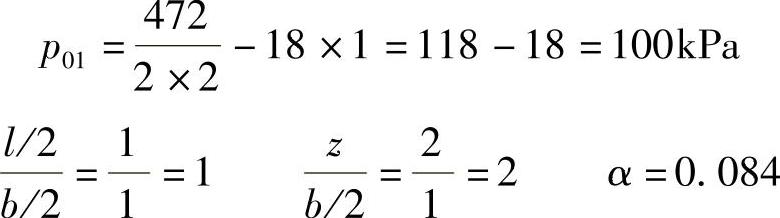
σ_z1=4αp₀=4×0.084×100=33.6kPa

（2）基础2：l=4m b=2m

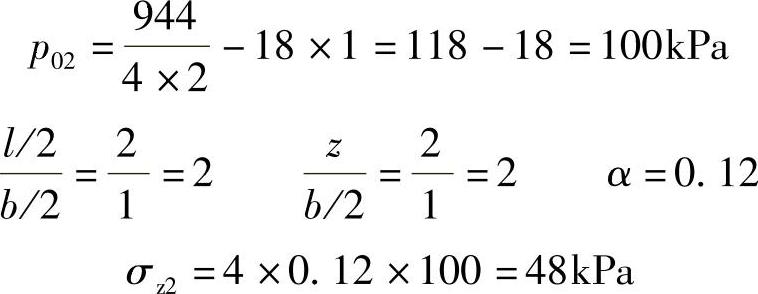
（3）基础3：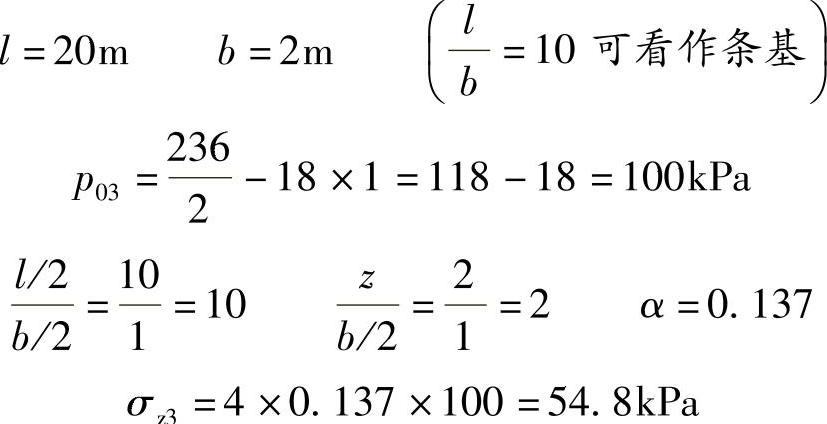

（4）讨论：比较此例题的计算结果可知，在其他条件相同（p₀相同，b相同，z相同）的条件下，地基中心点以下某点的附加应力随着基础长边与短边的比值增长而增大。因此，在基础设计施工中需要查明基础下一定深度范围的地基土是否存在有较软弱土层或其他异常情况，对于墙基础所需考虑的深度要比同宽度的柱基础深一些。

【3.4.6】 （2011年岩土考题）

如图3.4.6所示，在地面作用矩形均布荷载p=400kPa，承载面积为4m×4m。试求承载面积中心O点下4m深处的附加应力与角点C下8m深处的附加应力比值，最接近下列何项数值？（矩形均布荷载中心点下竖向附加应力系数a₀可由表3.4.3查得）

（A）1/2 （B）1 （C）2 （D）4

【答案】 （D）

【解答】 答题提示：本题附加应力系数表，是矩形均布荷载中心点下，而不是角点下的附加应力系数表。

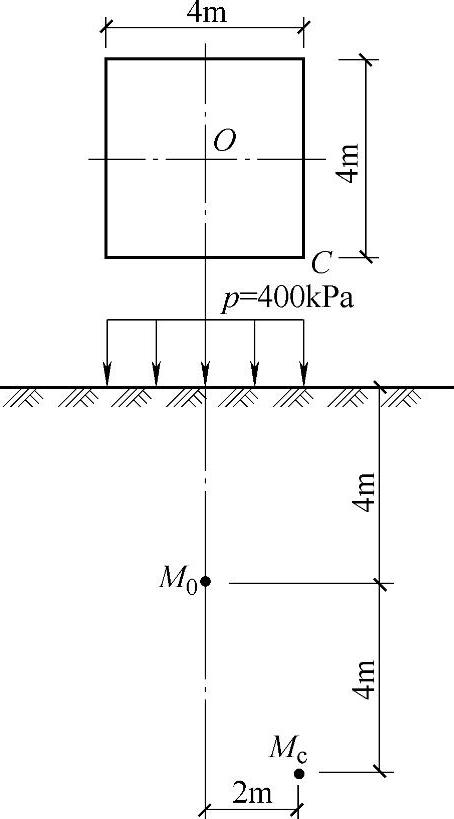
图3.4.6 应力计算示意图

求承载面积中心O点下4m深处的附加应力，查询附加应力系数时，用到的比值如下

l/b=1，z/b=1

查询表3.4.2，并线性插值，得承载面积中心O点下的附加应力系数为a₀=0.336

对于C点下8m深处的点M_C，由于上表无法查角点的附加应力系数，可以把C当成一个8m×8m大的矩形均布荷载的中心点，查表后将附加应力系数除以4即可。对于8m×8m大的矩形均布荷载作用下，l/b=8/8=1，z/b=8/8=1，查上表得a₀=0.336，于是点M_C的附加应力系数为a₀=0.336/4。

表3.4.3 附加应力系数a0

【3.4.7】 （2003年一级考题）

在同一非岩石地基上，建造相同埋置深度、相同基础底面宽度和相同基底附加压力的独立基础和条形基础，其地基最终变形量分别为s₁和s₂，试问，下列判断哪项正确？

（A）s₁>s₂ （B）s₁=s₂ （C）s₁<s₂ （D）不一定谁大谁小

【答案】 （C）

【详解】 就基底扩散面积而言，独立基础比条形基础大，因此，基底以下随深度变化的二者附加压力的收敛速度，独立基础较之条形基础要快，即基底以下同一深度处独立基础的附加应力比条形基础的附加压力小。所以，独立基础下地基最终变形量比条形基础下地基变形量要小。故（C）正确。

【简解】 相同埋置深度、相同基础底面宽度和相同基底附加压力的情况下，独立基础附加压力扩散面积大，所以独立基础下地基最终变形量比条形基础下地基变形量要小。

【3.4.8】 （2001年一级考题）

在非岩石的相同地质条件下，对于建筑物条形基础下的地基变形计算有下列四种论点。试判定哪一种论点是错误的？

（A）非承重墙可不作地基变形计算

（B）当两基础附加应力相等时，则基础底面宽度较大者，其最终沉降量较大。反之，基

础底面宽度较小者，其最终沉降量较小

（C）地基压缩变形与重量成正比，且与基础宽度无关

（D）当两个承受荷载大小不同的条形基础的埋深相同时，也可通过调整基础宽度的办法，

设计成使承受较大荷载的地基最终沉降量不大于承受较小荷载的地基最终沉降量

【答案】 （C）

【详解】 由《建筑地基基础设计规范》5.3.4条可知，砌体承重结构需满足地基变形允许值，非承重结构可不作变形验算。故（A）正确。

根据《建筑地基基础设计规范》5.3.5条式

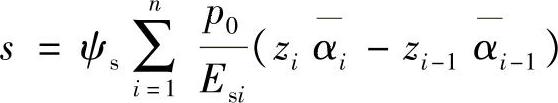
可以看出，地基最终变形量，与附加应力有关。当两基础附加应力相等时，由公式可以看出基础宽度越大，最终沉降量越大。故（B）正确。

重量越大，则地基附加应力越大，其地基变形量就越大。在同样的压力作用下，基础宽度越大，附加应力越小，则地基压缩变形越小。故（C）不正确。

当上部荷载大小不变，基础宽度越大，则附加应力越小，由公式可以看出，其地基变形量就越小，所以（D）的说法正确。

【简解】 重量越大，则地基附加应力越大，其地基变形量就越大。在同样的压力作用下，基础宽度越大，附加应力越小，则地基压缩变形越小。故（C）不正确。