自重应力分布曲线及其影响

1.基本假设与计算公式

由于土的自重产生的应力，称为自重应力。在一般情况下，土层的覆盖面积很大，所以土的自重可看作分布面积为无限大的荷载。土体在自重作用下既不能有侧向变形也不能有剪切变形，只能产生垂直变形（图3.1.1a），根据这个条件，均质土中的自重应力可按下式求得：

σ_cz=γz （3.1.1）

式中 σ_cz——地面下z深度处的垂直向自重应力（kPa）；

γ——土的天然重度（kN/m³）；

z——由地面至计算点的高度（m）。

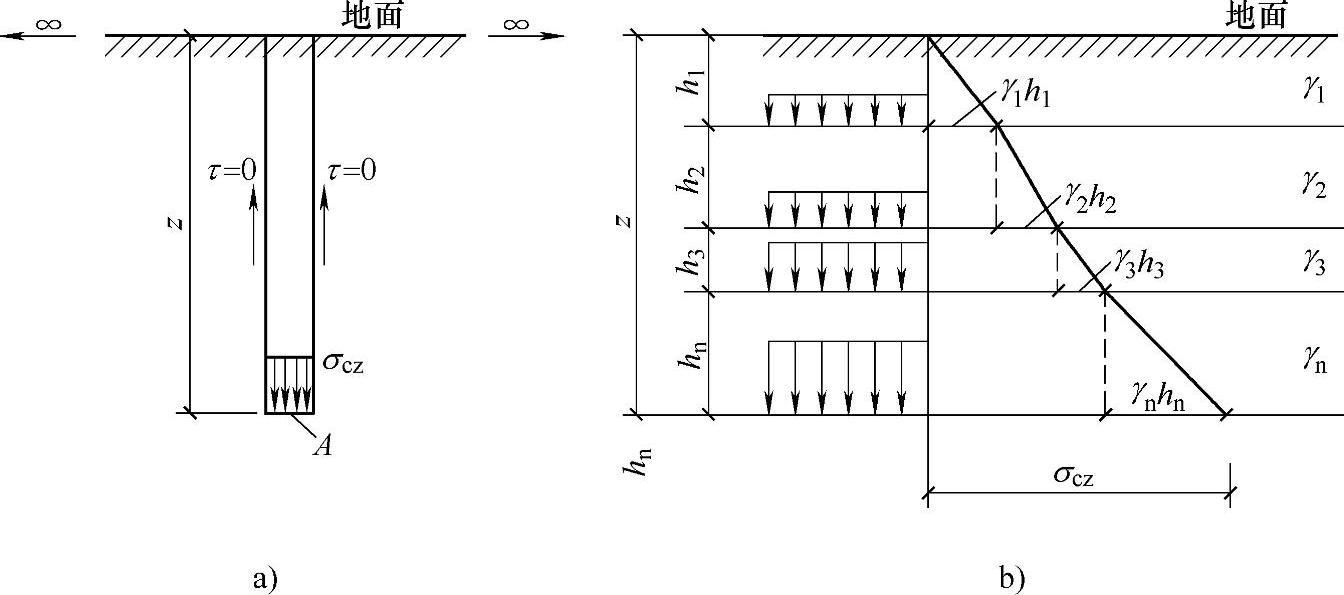
图3.1.1 自重应力的计算

a）计算简图 b）成层土的自重应力图

当地基由成层土组成（图3.1.1b），任意层i的厚度为h_i，重度为γ_i时，则在地面下深度为z处的自重应力σ_cz等于该处单位面积上土柱的重量，如下式所示：

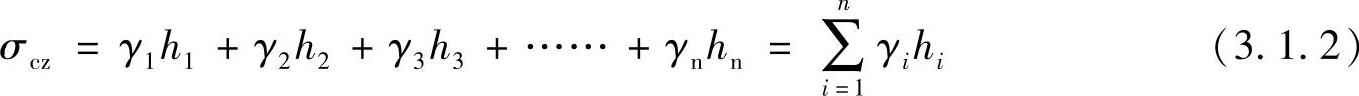
【3.1.1】 自重应力计算

条件：某地基土层如图3.1.2所示。

要求：求自重应力并绘出随深度分布图。

【解答】 自重应力计算见表3.1.1。

表 3.1.1

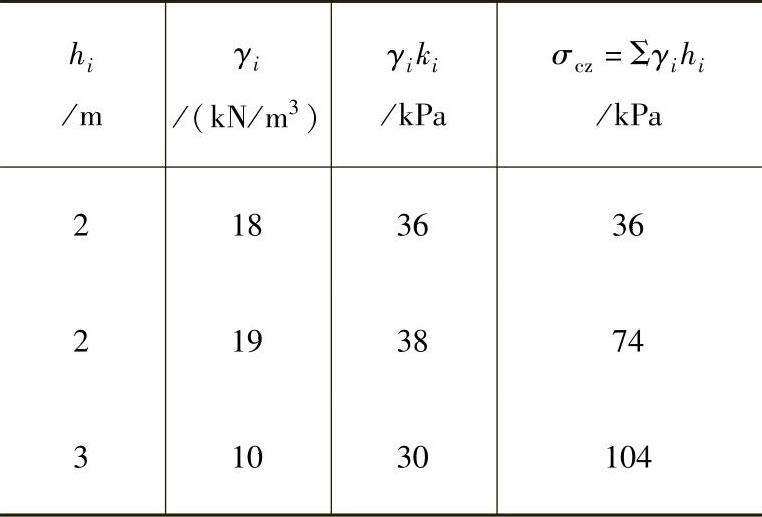
图 3.1.2

a）土层 b）σ_cz分布

2.地下水与不透水层的影响

（1）地下水的影响

地下水位以下的土层处于饱和状态，对于砂土或其他透水的土，由于土颗粒受浮力作用，计算自重应力时应采用土的浮重度γ′。这时地下水位面相当于土的一个分层面，在图3.1.3中，深度z处的自重应力为

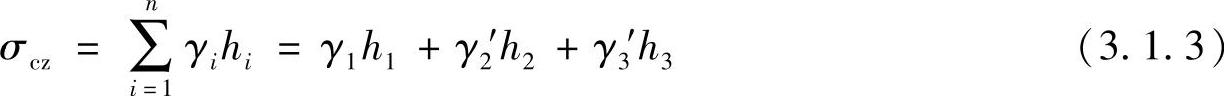
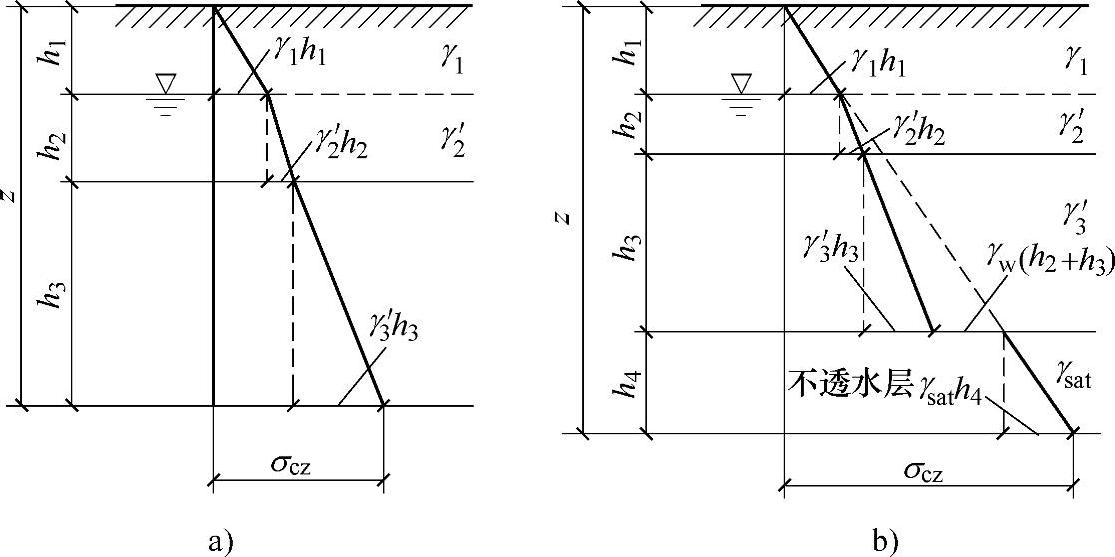
图3.1.3 土的自重应力分布

a）成层土，有地下水的情况 b）成层土，地下水下有不透水层的情况

黏性土则视其物理状态而定，一般认为，若水下的黏性土其液性指数I_L≥1，则土处于流动状态，土颗粒间存在着大量自由水，此时可以认为土体受到水的浮力作用；若I_L≤0，则土处于固体状态，故认为土体不受水的浮力作用；若0<I_L<1，土处于塑性状态时，土颗粒是否受到水的浮力作用就较难肯定，在实践中一般均按不利状态来考虑。

（2）不透水层的影响

不透水层一般为基岩或结构紧密的黏土层。地下水位以下的黏土层也处于饱和状态，由于土中的孔隙水几乎全部是结合水，土粒不受浮力作用，计算自重应力时应采用饱和重度。不透水层上表面处的自重应力等于全部上覆土和水的自重应力之和。在图3.1.3b中，不透水层顶面表面处的自重应力σ_cz为

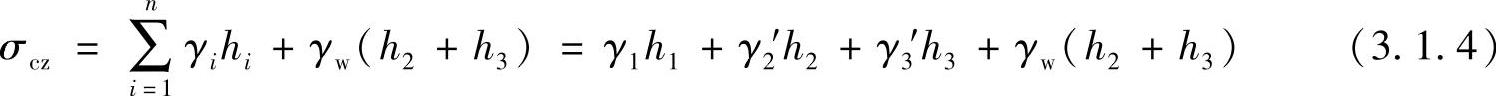
不透水层顶面以下的自重应力

σ_cz=γ₁h₁+γ₂′h₂+γ₃′h₃+γ_w（h₂+h₃）+γ_sat4h₄ （3.1.5）

图3.1.4将无地下水、有地下水和有地下水且存在不透水层的自重应力列在同一图中以便对比学习。

图 3.1.4

a）无地下水 b）有地下水 c）有地下水且存在不透水层

【3.1.2】 自重应力计算（有地下水）

条件：某地基的地质剖面如图3.1.5所示。

图3.1.5 自重应力分布曲线

要求：绘出自重应力分布曲线。(www.xing528.com)

【答案】 求不同重度分界面上土的自重应力大小。

耕植土层底面处：σ_cz=17.0×0.6=10.2kPa

地下水位处：σ_cz=10.2+18.6×0.5=19.5kPa

粉质黏土底面处：σ_cz=19.5+（19.7-10）×1.5=34.05kPa

淤泥质土底面处：σ_cz=34.05+（16.5-10）×2.0=47.05kPa

按一定比例在各分界面处水平位置上绘出自重应力大小，用直线连接可得图3.1.5所示自重应力分布曲线。

【3.1.3】 （2007年二级考题，原题是连锁题的子题，情境描述有所简化）

某柱下独立基础底面尺寸为4.8m×2.4m，埋深1.5m，如图3.1.6所示。土层分布自地表起依次为：黏土，厚度2.5m；粉质黏土，厚度2m；黏土，厚度4.5m。地下水位在地表下1.5m处。

试问，在基底中心点下7.5m处土的竖向自重应力（kPa），与下列何项数值最为接近？

（A）167.3 （B）139.5

（C）92.3 （D）79.5

【答案】 （C）

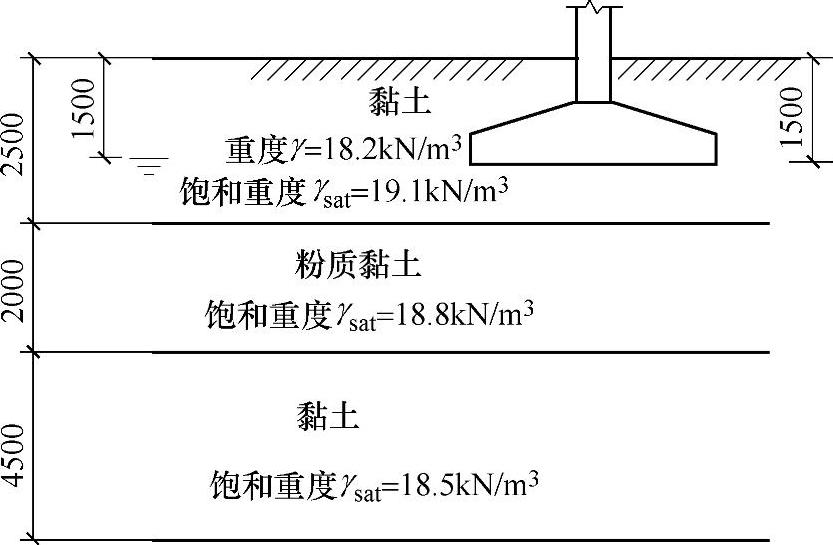
图 3.1.6

【详解】 作题提示：在自重应力计算时，自重应力从地面处算起，遇到地下水时取浮重度。竖向自重应力计算如下：

σ_cz=18.2×1.5+（19.1-10）×1+（18.8-10）×2+（18.5-10）×4.5=92.3kPa

故（C）正确。

【简解】σ_cz=18.2×1.5+（19.1-10）×1+（18.8-10）×2+（18.5-10）×4.5=92.3kPa

【3.1.4】 自重应力计算（地下水有升降）

条件：某工程地基如图3.1.7a所示，若地下水位从地表下1.5m迅速降到4.5m，假定降水后土的重度不变。

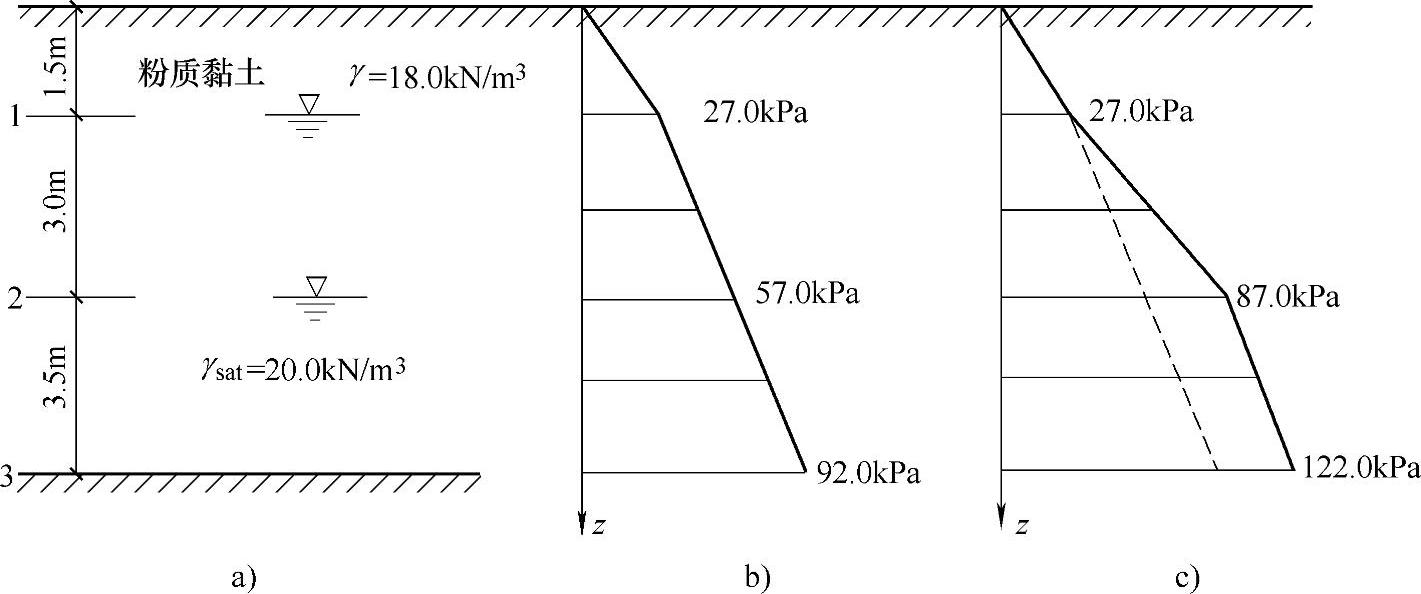
图 3.1.7

a）土层分布 b）降水前自重应力分布 c）降水后自重应力分布

要求：试作水位下降前后粉质黏土层中土的竖向自重应力分布图。

【解答】 粉质黏土层中自重应力计算过程和结果列于表3.1.2。

表3.1.2 自重应力计算

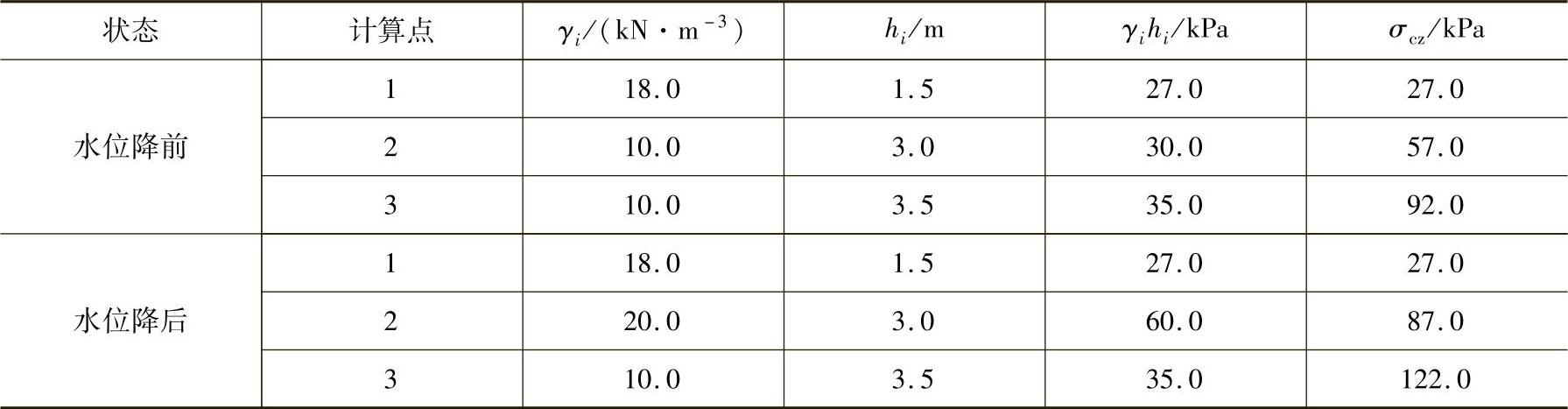
从本例题可以得出如下结论：

地下水位以上土的自重应力用天然重度计算。地下水位以下的土受到水的浮力作用，减轻了土的有效重力，计算时应该取土的有效重度γ′代替天然重度，有效重度等于饱和重度减去水的重度。用有效重度计算的自重应力实际上反映作用在土骨架上的应力，称为有效自重应力。有效自重应力与水压力的合力称为总自重应力。降低地下水位，会使地基中的自重应力增加，从而引起地基产生附加沉降变形。

实际上，当地基中存在着地下水时，土中的骨架和孔隙水分别受力，形成了两个独立的受力体系。两个力系各自保持平衡且又互相联系。

现通过图3.1.8a所示的水面位于地面以上的情况来讨论。现取一个竖直柱体进行分析，在截面a—a上作用着由截面上方柱体中土和水的自重产生的作用力P。为了分析P值在土骨架和孔隙水上的分布情况，将a—a截面放大，如图3.1.8b所示，可以看到该截面由孔隙水与土颗粒两种材料组成。为更清晰地说明力的传递情况，设想将分散的颗粒集中为一个大颗粒，如图3.1.8c所示。由力的平衡条件可得：通过a—a面传递的总压力，由通过a—a面上土颗粒传递的压力和通过a—a面上孔隙水传递的压力共同向下传递。通过土骨架传递的应力，称土骨架应力（也称粒间应力）；通过孔隙水传递的压力，称孔隙水压力（或应力）。这是土力学中十分重要的两种力系之间的关系，即土中一点的总应力是该点粒间应力与孔隙水压力之和。所以，地下水位以下土层中土骨架产生的自重应力等于土的浮重度乘以相应的土层厚度。

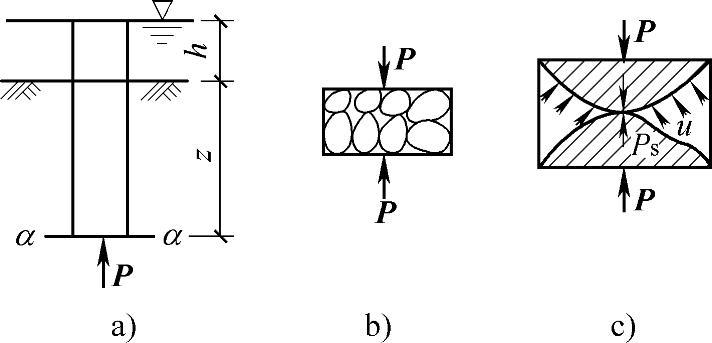
图3.1.8 自重应力的骨架孔隙水应力的分析

图3.1.9 地面有满布压力时土中自重应力

a）地面有满布压力 b）将满布压力化为换算土层

3.满布荷载的影响

如图3.1.9a所示，如果地面上满布着荷载q（例如大面积的水），则在深度为z的水平面上，除了土的自重应力γz外，还有满布荷载压力q，总的应力为

σ_cz=γz+q（ 3.1.6）

由于q是满布的，它的力学作用就相当于在原地面上增加了一层厚度为h=q/γ的土，h叫做换算土层厚度，如图3.1.9b所示。这样在原地面以下z处的应力为

σ_cz=γ（z+h）=γ（z+q/γ） （3.1.7）