新型复合材料受弯构件分析方法及变形分析

对木材、竹材这样的新型复合材料，受弯构件的极限状态分析方法还没有建立。例如，现行木结构受弯构件的计算方法仍采用线弹性材料力学计算方法。而重组竹材料在单轴受压应力状态下表现出了很强的非线性应力—应变关系，因此，重组竹梁的弯曲必然呈非线性破坏特征。故线弹性理论不能应用于重组竹受弯构件极限状态分析。

1.破坏形态与破坏机理

由于重组竹梁是在横向逐层铺设竹篾压制而成的，截面层状之间的界面力学性能比较复杂，加载后沿层界面会产生法向应力，使层状逐渐剥离，从而产生细微的裂纹；随荷载增加，裂纹沿层界面慢慢展开，同时材料达到比例极限值；当荷载超过比例极限时，材料进入塑性阶段，梁顶部开始出现受压屈曲，梁中和轴以下部位开始出现水平裂纹，这些裂纹随荷载增加不断向两端扩展，并且伴随新的裂纹产生；当荷载接近极限值时，伴随竹界面剥离的响声，微裂纹沿层界面迅速扩展，形成宽裂缝，裂缝以下的竹束达到材料抗拉强度后被脆性拉断，梁宣告破坏。

重组竹梁弯曲破坏呈非线性渐进破坏特性。首先，梁上部纤维受压屈曲；其次，受拉区纤维束之间发生界面分离，形成平行于纤维方向的纵向裂纹，这些裂纹随外荷载的增加不断扩展，宽度逐渐增大；最后，梁下部纤维束拉断，梁丧失承载能力。梁在整个受力过程中，荷载—位移曲线首先呈线性关系；随着梁跨中裂纹的出现、发展，荷载—位移曲线逐渐偏离直线状态，直至极限荷载梁有较长的非线性段。竹梁破坏前，截面应变沿高度方向基本上呈线性变化，因此在竹梁受弯构件设计计算时，梁的受弯破坏截面符合平截面假定。

构件在破坏之前，都会断断续续地出现竹纤维束断裂或压屈分层的响声，破坏过程并不突然，并且破坏时梁的整体变形十分显著。总体来说，重组竹梁作为受弯构件的破坏征兆比较明显，这对于重组竹梁在房屋结构中的应用很有意义。

2.承载力计算

为了得出重组竹梁极限受弯承载力及非弹性变形计算公式，假定梁的受弯破坏截面承载力极限状态为：

（1）符合平截面假定，即梁在弯曲变形过程中，横截面始终保持为平面，并且与梁轴线垂直；

（2）对于重组竹中的胶层，不考虑其厚度，并假定其力学性能与竹（木）相同；

（3）不考虑材料各向异性的影响，构件的受弯性能主要由材料顺纹方向的力学性能决定，并且忽略剪切效应；

（4）忽略截面应力分布沿构件厚度方向的变化，将平面内弯曲简化为平面应力问题；

（5）材料受拉时为线弹性体，受压时分为弹性和塑性两部分。

根据以上假定，极限状态下梁截面的应力、应变分布如图6-16所示，中性轴以下部位为构件受拉区，破坏截面受拉区外侧纤维达到抗拉极限强度；中性轴以上部位为构件受压区，材料经历了弹性受压、原始裂纹扩展、纤维与基体剥离、纤维屈曲、基体压溃等复杂的非线性渐进过程，最终外侧纤维压屈，材料达到抗压强度极限值。受弯构件破坏截面可分为三部分，即：

（1）中和轴以下的受拉部分（A），材料线性受拉；

（2）中和轴以上的弹性受压部分（B），材料线性受压；

（3）中和轴以上的塑性受压部分（C），材料应力与应变呈二次曲线关系。

图6-16 受弯构件横截面应力、应变分布图

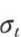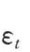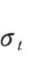图中，为材料的受拉强度，分别为材料的比例极限和抗压强度；为对应的拉应变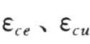，分别为对应的压应变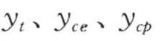；分别为受拉区、弹性受压区和塑性受压区的高度。由图6-16还可以看出，在求解梁、柱非弹性极限承载力时，构件的塑性受压区只考虑材料的非线性强化阶段。

根据以上构件破坏模式的分析，结合平截面假定，即截面任一点纵向应变 与该点至中性轴距离y成正比，以及材料的线弹性本构关系及非线性应力—应变关系，构件截面的应力分布可表示为

式中：E——材料弹性模量；

φ——构件弯曲曲率；

б（y）——材料非线性强化阶段的应力—应变关系。

如图6-16所示，受弯构件由力的平衡条件，得

根据式（6-8），式（6-9）可以写成

考虑弹性受拉区和弹塑性受压区之间的关系为

根据受拉区与受压区高度的几何关系，有(www.xing528.com)

结合式（6-10）、式（6-11）和式（6-12），即可求解yt、yce、ycp的值，分别为

式中：

α是采用矩形分布来替代实际应力分布所引起误差的修正系数。当材料为理想弹塑性时，α＝1；当基于本书设定的非线性应力—应变函数关系式时，α＝1.33。故此处的修正系数α一般与材料的本构关系相关，而与塑性受压区高度无关。修正系数α的定义基于构件破坏时受压区边缘材料达到抗压极限强度，这与实际状态会有一定误差。但对于竹木结构材料，在受弯、压弯构件的极限状态下，破坏截面受压区最外层材料强度与抗压极限值比较接近，故这种简化产生的误差可以接受。

将бt＝бtu代入式（6-13）可以得到构件极限状态下，破坏截面的受拉区以及弹、塑性受压区高度，从而求得各区间的应力分布。同时，利用式（6-13）还可以得到构件整个加载过程的截面应力分布变化情况。

根据构件截面破坏模式分析，极限状态下梁的破坏表现为：截面顶端材料压屈，达到抗压极限值бcu；截面底部材料拉断，达到抗拉极限值бtu，则极限状态时，梁截面弯矩为

式中：Фu——构件极限状态下的弯曲曲率。

令截面塑性受压区的压应力产生的弯矩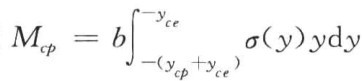，根据平截面假定，有ε（y）＝Фuy，将其代入非线性强化阶段的应力—应变函数关系式，则有

结合式（6-16），对Mcp进行积分，得

结合弹性阶段截面正应力产生的弯矩，则受弯构件的极限弯矩为

式中，构件极限状态下的弯曲曲率Фu是处于非线性阶段的曲率，可依据极限状态下受拉区的应力—应变仍服从胡克定律，故

式中：бtu——构件极限状态下抗拉极限强度；

ytu——构件极限状态下弹性受压区高度。

图6-17给出了受弯构件弯矩—曲率关系曲线，从中可以看出，弹性阶段，M-φ呈线性关系；进入弹塑性阶段，M-φ关系曲线是非线性的，此时EI不能作为一个常值。这再一次说明了竹（木）梁—柱构件的计算不能简单地按照弹性理论方法思考，需要考虑到材料应力—应变关系的非线性特性。

图6-17 受弯构件的弯矩—曲率关系曲线

3.变形分析

利用对称性，梁的变形分析可采用图6-18所示的模型。

图6-18 梁变形分析模型

假定梁的纯弯段处于塑性状态，而剪跨段处于弹性工作状态，它们的曲率分别为kp和ke。则梁的挠曲线满足下述微分关系

考虑到曲率与弯矩之间的关系，上式可以写成

通过边界条件和连续性条件

得到梁挠曲线方程为

式中：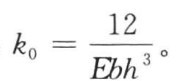

若梁的纯弯段亦处于弹性工作阶段，考虑x＝α处连续性条件可得纯弯段的曲率

以式（6-23）中的kem代替式（6-22）中的kp得到梁处于弹性工作阶段时纯弯段的挠曲线方程为