针对破裂面为直线的形式,考虑地震力和裂隙中静水压力计算锚固边坡的地震稳定性,具体见图4.12所示。其中H为边坡高度,H1为坡顶后缘裂隙深度,H2为潜在滑裂面高度,zw为裂隙中水柱高度,Pw1为裂缝中的静水压力,Pw2为潜在滑裂面上的静水压力,kh(t)为质心处水平地震系数,kv(t)为质心处竖向地震系数,G为潜在滑体重量,T1、T2、T3为锚索预应力,θ为滑裂面倾角,ψp为边坡坡角。根据边坡体的几何尺寸和岩土体材料的力学参数可求得锚索预应力、破裂面黏聚力、静水压力、水平地震力、竖向地震力和重力在速度v上的功率。
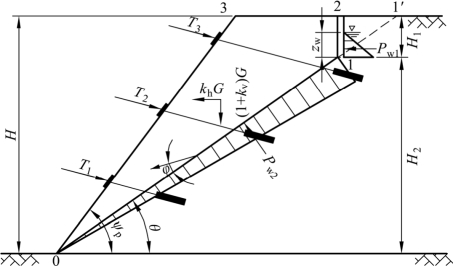
图4.12 预应力锚索加固直线形破裂面示意
1.锚索预应力做功
由图4.12知预应力锚索提供的阻滑力T(t)

阻滑力T(t)与塑性势速度v之间的夹角θ1
![]()
阻滑力T(t)在速度v上所做的功率W1为负功,起到阻止边坡下滑的作用
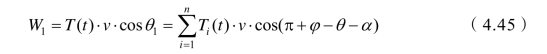
2.黏聚力做功
直线型破裂面上的黏聚力c与塑性势速度v之间的夹角θ2
![]()
黏聚力c在速度v上所做的功率W2为负功,起到阻止边坡下滑的作用
![]()
3.静水压力做功
裂隙中静水压力由两部分组成,分别为坡顶后缘裂隙中的静水压力Pw1和潜在滑裂面上的静水压力Pw2,按下式计算

静水压力Pw1与塑性势速度v间的夹角θ3
![]()
静水压力Pw1在速度v上所做的功率W3为正功,引起边坡下滑
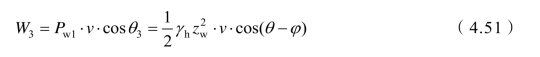
静水压力Pw2与塑性势速度v间的夹角θ4

静水压力Pw2在速度v上所做的功率W4为正功,引起边坡下滑

4.滑体重力做功(https://www.xing528.com)
由图4.12所示边坡体的几何特征知单位宽度滑体重量G

竖向重力G与塑性势速度v间的夹角θ5

竖向重力G在速度v上所做的功率W5为正功,引起边坡下滑

5.地震力做功
滑体中的地震力由两部分组成,即水平向地震力kh(t)G与竖直向地震力kv(t)G,与塑性势速度v间的夹角分别为θ3、θ5,其在速度v上所做的功率为正功,引起边坡下滑。
水平地震力W6可按下式求解
![]()
竖向地震力W7可按下式求解
![]()
滑裂面上摩擦力与法向反力的合力与塑性势速度v间的夹角为π/2,见图4.13所示,故其做功为零。
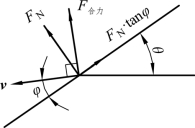
图4.13 滑裂面上法向反力与摩擦力做功示意
根据正功与负功的关系得到锚固边坡的稳定系数K,即阻止边坡下滑做功与引起边坡下滑做功之比
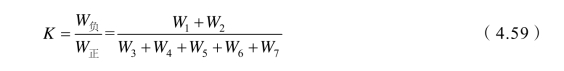
将式(4.45)、式(4.47)、式(4.51)、式(4.53)、式(4.56)、式(4.57)、式(4.58)代入式(4.59),化简得
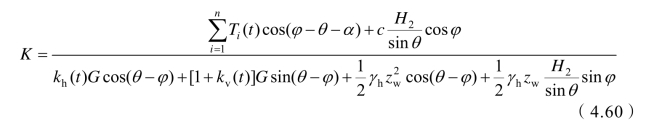
若将地震作用过程中每一时刻的加速度响应值代入式(4.60)即可得到锚固边坡的安全系数时程曲线。现阶段工程设计都是基于安全系数的概念,即一旦边坡的安全系数小于1则认为产生失效破坏,而实际震害调查及前章振动台模型试验均显示,当边坡安全系数小于1时上部滑体将产生沿潜在破裂面的向下位移,但锚固边坡的稳定性仍然能够得到保证,这也说明现有的安全系数法过于保守。本节根据地震过程中边坡响应加速度是否存在超过其临界加速度的状况建立滑动位移求解方程,再由边坡位移引起的锚索轴力改变值评价锚固体系的安全性能。
若在地震过程中,地震加速度时程曲线中出现了大于屈服加速度的时间段,此后边坡体将沿潜在破裂面出现向下的滑动位移。对于滑动的边坡体而言,产生滑动时的地震惯性力可分解为刚达到屈服加速度时的惯性力(这部分与滑体重力、黏聚力、静水压力等做功相抵消)和超过屈服加速度部分产生的惯性力这两部分。根据达朗贝尔原理,滑块在运动过程中假设一虚拟惯性力,在其作用下滑体仍处于平衡状态。若不考虑竖直方向的地震力变化,可得水平地震动超出屈服加速度部分所做的功率为Wy,虚拟惯性力做功为Wv,即
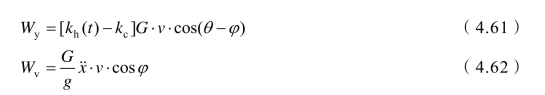
式中 kc ── 水平向屈服加速度系数;
x˙˙ ── 沿滑面的加速度。
令功率Wy与功率Wv相等,得到上部滑体沿潜在滑裂面的位移x
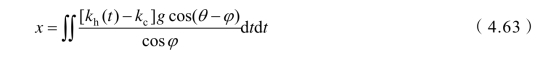
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




