振动台试验结果对框架锚索加固边坡地震动特性的影响

本节以第3章振动台模型试验为例，验证锚索轴力地震响应理论值求解结果的正确性。选取加载地震波峰值为0.564g时的人工波，通过坡脚自由场处的加速度时程曲线计算模型试验中编号T1的锚索轴力残余值时程曲线，如图4.9（临界加速度为0.5g，计算见第4.2节）所示。由图知锚索轴力残余值增加量约为3N，与模型试验测得的轴力增长值2.5N基本一致，具体计算程序见表4.8。分析产生这种差异性的原因是在位移响应时程计算过程中未 考虑锚索轴力改变对边坡临界加速度的影响，导致位移响应值计算结果略大于实际地震响应值。

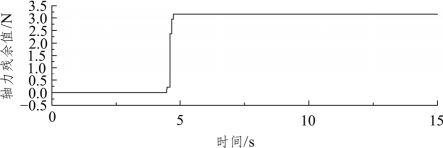
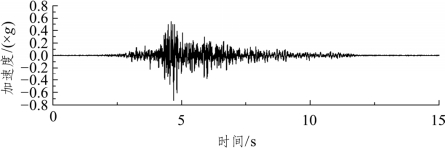
图4.9　地震下轴力残余值时程曲线

表4.8　锚索轴力残余值Matlab计算程序

对于第3章框架锚索加固边坡的振动台试验模型而言，ki＝120 kN/m、mi＝2.4 kg，假设其形函数ψ呈线性分布，由公式（4.15）得

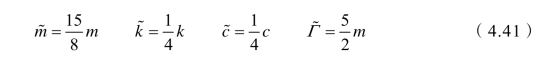
将式（4.41）带入式（4.16）得

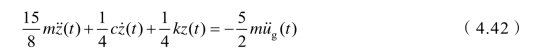
为求解式（4.42），本节取地震波采样频率的时间间隔Δt＝0.002s，依据动力反应的数值计算方法编制Matlab程序（表4.9）求解广义位移的响应时程曲线，将其结果带入式（4.40）得到T1测点的锚索轴力弹性响应值，见图4.10所示。(www.xing528.com)

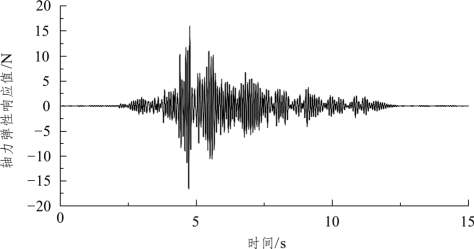
图4.10　广义单自由度体系计算的轴力弹性响应时程曲线

表4.9　地震波作用下的轴力弹性响应的Matlab计算程序

续表

将上述求解的锚索轴力残余值响应时程曲线与锚索轴力弹性响应值时程曲线叠加，与振动台模型试验时实测的T1测点轴力响应时程曲线进行对比，具体见图4.11所示，可见本节提出的理论计算方法不论是轴力峰值还是轴力残余值都大于实测结果，但两者的差别较小，因此可认为地震工况下根据本节计算方法所得的轴力响应时程曲线与实测结果吻合，为地震波作用下锚索轴力动态响应值的计算提供了一种理论计算方法。

图4.11　T1测点锚索轴力计算结果与振动台试验实测值

由于实际边坡锚固工程在设计时常考虑了较大的安全系数，在经历地震后，如汶川地震震害调查成果中^{[4] [5]}仅有个别锚固体发生锚固系统失效的情况，因此建议在地震过后锚固系统的安全性评价时仍采用现阶段的规范设计方法。