锚索轴力地震响应值计算方法-地震动特性研究

地震作用过程中锚索轴力的变化值可以按两种情况考虑：① 边坡无残余变形时，锚索轴力在地震作用前和地震结束时刻一致，只是在地震激励过程中产生动应力，这时可按结构动力学方程求解地震作用过程中的锚索轴力时程响应曲线；② 边坡产生滑移变形，此时锚索自由端轴力在地震结束时刻大于地震前，假设边坡为刚性块体滑移，锚索轴力的地震响应值可按弹性动态响应值与残余变形引起的轴力增量这两部分叠加组成。

1.轴力弹性响应值

对于框架锚索加固边坡，地震时框架梁结构与边坡体变形是协调一致的，锚索轴力的地震响应值可通过先求解框架梁结构的位移响应值[16]，再根据锚索钢材的力-位移换算关系得到锚索轴力的时程曲线；而对于无框架结构的锚垫墩加固边坡，锚头处的地震响应与边坡岩土体一致，参考土坝坝体多质点体系[17]建立其在地震作用下的运动方程进而求得锚索轴力响应值。本节将分别对这两种情况下的锚索轴力进行地震响应值求解。

1）框架锚索加固边坡

框架锚索加固边坡时框架梁与边坡体的相互作用见图4.2所示。首先对框架梁进行分块，即以框架梁节点为中心，上下各取框架梁竖向间距的一半做质量集中，见图4.2中编号1、2、…、n所示，此时框架梁结构成为一个具有集中质量的多自由度体系，根据结构动力学理论求出框架梁各节点在地震时的位移响应值。

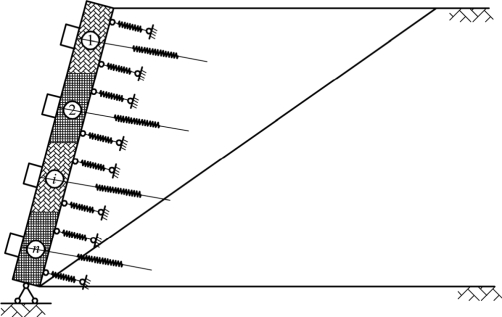
图4.2　框架梁与边坡体相互作用的简化示意

取框架梁结构中的第j块，见图4.3所示，建立其地震运动方程。假设框架梁第j层相对于坡脚地面的位移可表达为

式中 ψj ── 定义偏转形状的位移形函数；

u j(t) ── 第j层相对位移；

z j(t) ── 广义位移。 则，第j层梁体的绝对位移为

第j层梁体与j+1层间的剪力fSbj通过层间刚度kj与层间相对位移Δj＝uj－uj+1存在的关系如下：

其中，层间刚度为

式中 EI ── 框架梁柱的弯曲刚度；

lj ── 第j层梁体的长度。

第j层梁体与j+1层间的阻尼力fDbj通过层间阻尼系数cj与层间相对速度存在的关系如下

对于第j层梁体，它在地震作用过程中的每一瞬时，在内部的层间剪力fSbj、阻尼力fDbj、假想的惯性力、地基反力和锚索轴力的共同作用下处于平衡状态，其中地基反力和锚索轴力在水平方向上大小相等、方向相反。根据虚位移原理，建立框架梁体的运动方程。假设第j层框架梁体发生虚位移juδ，则外力在虚位移上所做的外力虚功

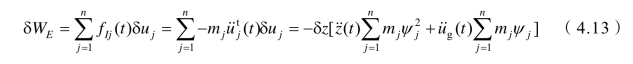
层间剪力和阻尼力在经历与虚位移相关的层间位移时所做的内力虚功

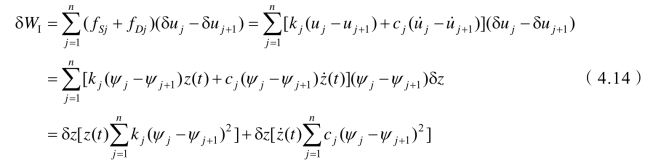
因外力虚功和内力虚功相等，消去δz后可得

令

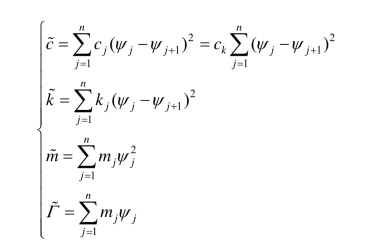
则，式（4.15）可化为标准形式的运动方程

假设框架梁结构的密度为ρk，纵梁的截面尺寸为a b×，横梁的截面尺寸为c b×，将纵梁由坡顶向下依次划分为n段，则

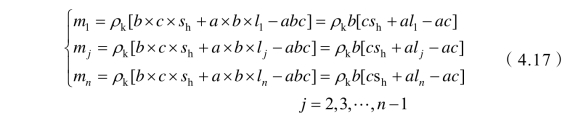
其中

由上述求解过程可得到地震时框架梁第j层的位移响应值，再将其代入式（4.19）即可求得锚索轴力的响应时程。

式中 ΔTj(t) ── 锚索轴力的地震响应增量；

lj ── 第j孔锚索自由段长度；

Ej ── 第j孔锚索的弹性模量；

Aj ── 第j孔锚索的横截面积；

α ── 锚索的锚固倾角。

由上述推导可知，地震时框架锚索加固边坡的锚索轴力弹性响应值的求解步骤为：

① 对于给定的框架梁截面尺寸、节点高度、密度、边坡高度以及坡度等相关参数，将其带入式（4.17）、式（4.18）求得框架梁结构体系的集中质量分布。

② 假设框架梁沿高度方向的形函数、各分层的黏滞阻尼系数和剪切刚度，将其带入式（4.15）、式（4.16）求得在给定的地震荷载作用下的动力方程，计算出地震时框架梁各节点处的位移响应时程。

③ 将步骤②中的位移时程代入式（4.19）求得地震作用过程中框架锚索加固边坡体处于弹性阶段时，锚索自由段的轴力响应时程。

2）锚垫墩加固边坡

锚垫墩加固边坡时，将坡体从上到下依次划分为n个集中质量，其中每一集中质量在坡面的中心为锚头出露处，具体见图4.4所示，选择第i块土体进行地震作用时的受力分析，具体见图4.5所示。根据牛顿第二定律可得地震情况下第i块土体的运动方程，即

式中 mi ── 第i块土体质量；

üi(t) ── 第i块土体的加速度；

ci ── 第i块土体的阻尼系数；

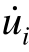(t) ── 第i块土体的速度；

ki ── 第i块土体的剪切刚度；

ui(t) ── 第i块土体的位移；

ΔTi(t) ── 锚索轴力的地震响应增量，其与ui(t)的关系见式（4.19）。 定义第i孔锚索的刚度系数为ik′，则

将式（4.19）、式（4.21）带入式（4.20），得

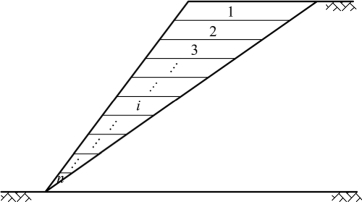
图4.4　边坡集中质量体系

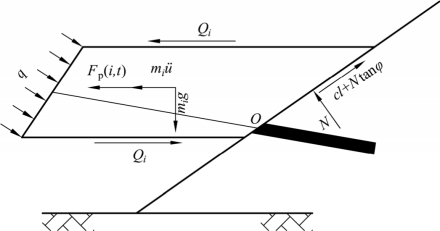
图4.5　第i块土体受力示意

对于多质点体系，将节点的相对位移、相对速度和相对加速度分别记为向量，即

（1）质量分量矩阵。

假设边坡高度为H、滑裂面后缘距坡面距离为L、锚索框架梁的水平间距为sh、竖直间距为sv、岩土体密度为ρs、第i块土体锚头距坡脚的竖直距离为hi，则第i块土体的质量为

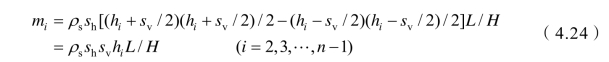(www.xing528.com)

编号为1的土体质量为

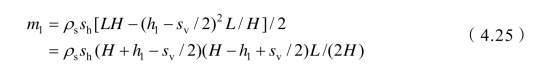
编号为n的土体质量为

由式（4.24）～式（4.26）得到多质点体系的质量分量矩阵M

（2）刚度分量矩阵。

地震时第i块土体与相邻土体间的相互作用见图4.6所示，则第i块土体的层间刚度为

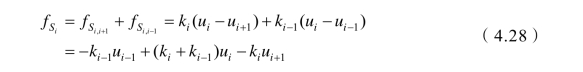
编号为1的土体层间刚度为 编号为n的土体层间刚度为

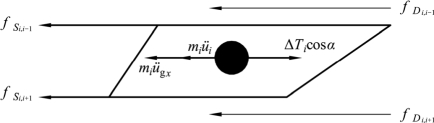
图4.6　相邻土体相互作用示意图

由式（4.28）～式（4.30）得到多质点体系的刚度分量矩阵K1

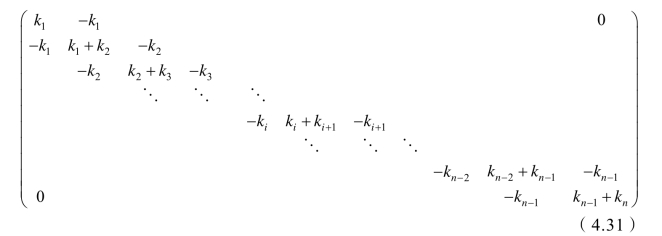
考虑锚索的刚度系数，由式（4.22）得锚索加固滑体的刚度分量矩阵K

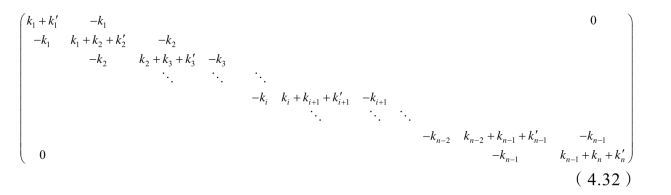
其中：k1，k2，k3，…，kn与划分的各土层的几何形状和物理力学性质有关，参考坝体剪切刚度^[3]的定义，得第i块边坡土体的剪切刚度

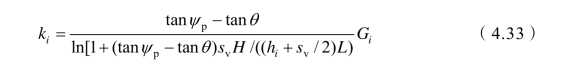
式中 Gi ── 第i块土体的剪切模量；

ψp ── 边坡坡角；

θ ── 滑裂面倾角。

（3）阻尼分量矩阵。

边坡集中质量体系的阻尼系数采用经典阻尼矩阵中的Rayleigh阻尼[16]，即

式中 α0 ── 质量比例阻尼系数（s－1），由公式（4.35）计算；

β0 ── 刚度比例阻尼系数（s），由公式（4.35）计算。

式中 ζ ── 阻尼比，通常取5%；

ω ── 自振频率，通常取第一阶振型的自振频率，即

式中 Si ── 分层土层的厚度；

G ── 分层土层剪切模量Gi的加权平均值，对于均质边坡而言，G为常数；

ρ ── 分层土层密度ρi的加权平均值，对于均质边坡而言，ρ为常数。

将上述（1）、（2）、（3）中的质量分量矩阵、刚度分量矩阵和阻尼分量矩阵带入公式（4.22），得到多自由度体系在地震引起的地面运动作用下的控制微分方程，即

式中E可由下式表示

对于任意给定的地面地震加速度时程曲线，将式（4.27）、式（4.32）、式（4.34）、式（4.38）代入式（4.37），即可求得边坡体各土层在弹性阶段的位移响应时程曲线。概括起来，上述锚垫墩加固边坡的位移响应时程求解步骤如下：

（1）以锚头的出露位置为中心，将边坡进行竖向分层计算集中质量，集合组成质量矩阵。

（2）求解分层岩土体的剪切刚度和锚束体的抗拉刚度，集合组成刚度矩阵。

（3）按照Rayleigh阻尼求解体系的经典阻尼矩阵。

（4）将给定的地震加速度时程曲线按照傅里叶变换分解成若干个简谐波，求解简谐波作用下集中质量体系的位移时程。

（5）叠加步骤（4）中求得的位移时程，进而得到给定的地震加速度作用时边坡体的位移响应时程。

（6）将步骤（5）中各时段的位移带入式（4.19），求得地震作用过程中边坡体处于弹性阶段时的锚索自由段轴力响应时程。

综合比较框架锚索加固边坡和锚垫墩加固边坡的锚索轴力响应值求解过程知，后者涉及的参数较多，且岩土体参数的变异性较大，部分参数需采取经验取值，容易造成较大的误差。而钢筋混凝土框架梁结构体系的动力参数取值较稳定，且动力求解过程中避免了相关刚度矩阵、阻尼矩阵的集合，使计算过程得到合理的简化，方便工程实际应用。对于多级框架锚索支护结构体系，在式（4.16）计算时若将各级边坡平台处的üg(t)值乘以其相对坡脚的加速度放大系数，可考虑加速度放大效应对锚索轴力响应时程的影响。

2.轴力残余值

地震结束时刻锚索轴力的增加值与锚头-基岩内灌浆体的位移响应差值有关，通常基岩在地震过程中始终处于弹性响应阶段，地震结束时锚索轴力出现增加的现象必定伴随着相应位置边坡体残余变形的出现。为确定边坡体在地震作用过程中是否产生残余变形及计算残余变形值的大小，我们采用Newmark滑块理论[18]来计算边坡体在给定地震荷载作用下的变形值，具体见3.2节，然后按下文求解锚索轴力增加值。

刚性块体沿潜在破裂面的滑动见图4.7所示，假设张拉锁定后的锚索自由段长度为lf（即ob段），地震作用过程中上部块体沿潜在滑动面产生了刚性滑移量x（即bb′段），锚固倾角与水平面夹角的变化值为Δα（即∠bob′），锚索自由段长度变为fl′，则相较于地震前，锚束体的伸长量为

因锚索伸长量引起的轴力增加值为ΔTi，即

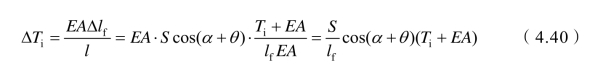
式中 E ── 锚束体的弹性模量（MPa）；

A ── 锚束体的横截面积（mm2）；

Ti ── 初始预应力（N）；

α ── 锚固倾角（°）；

θ ── 滑裂面与水平面的夹角（°）。

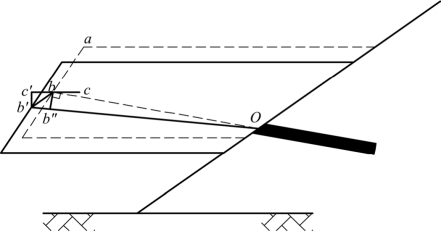
图4.7　刚性块体滑移示意

在实际地震作用下，当地震加速度大于临界加速度时边坡体开始出现残余变形，因锚索与边坡岩土体的变形相协调，残余变形的出现必将引起锚索轴力增加，进而导致边坡体临界加速度的提高。鉴于地震作用过程通常较短暂，为简化计算过程且偏于保守设计，本节在计算给定地震波作用下的边坡体的残余变形值时认为其临界加速度值不变。刚体滑移阶段锚索轴力量值增加的时程曲线可按如下步骤求解：

① 已知边坡体及锚固系统的相关参数，将其带入第4.2节求解锚固边坡体的临界屈服加速度kc。

② 对于给定的地震加速度时程曲线，对超过临界屈服加速度部分进行积分，求解边坡体的残余变形时程曲线，具体见图4.8所示。

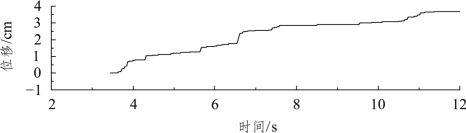
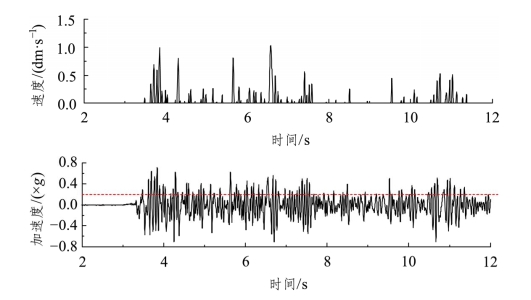
图4.8　加速度时程曲线求解永久变形值

③ 针对不同高度处的锚索，根据式（4.40）计算每孔锚索轴力ΔT（t）随时间的变化值，即锚索轴力残余值的时程曲线。

综上可知，将本节第1点中求得的锚索轴力弹性响应时程与本节求得的锚索轴力残余值增加量叠加后即可求出在给定地震波作用下的锚索轴力响应时程曲线。为验证本节提出方法的正确性，下节将其计算结果与第3章振动台模型试验测试结果进行比较。