智能车辆行为决策模型与安全评估结果分析

通过对采集的数据进行预处理并进行统计分析后得到共计21 个变量（见表5-2），其中驾驶模式为分类变量，剩余20 个变量为传感器或者统计得出的属性变量。为了能够得出对人机共驾智能车系统驾驶模式决策具有显著性影响的属性，本研究采用助理人员记录的300 例不同类型数据为研究对象，以驾驶人自汇报的驾驶模式结果为分类属性，进行人机共驾智能车系统决策属性挖掘。

表5-2　数据采集类型及详细参数

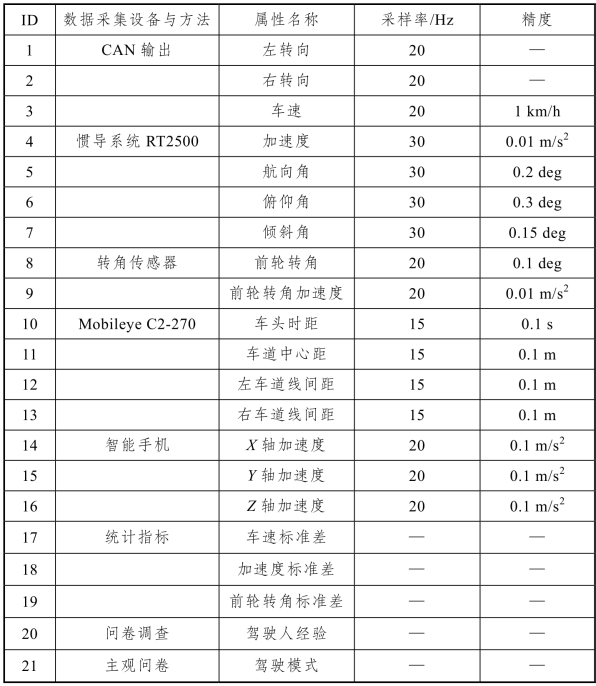
在表5-2 中，车速标准差、加速度标准差、前轮转角标准差是通过计算得出的，其计算方法[95]：

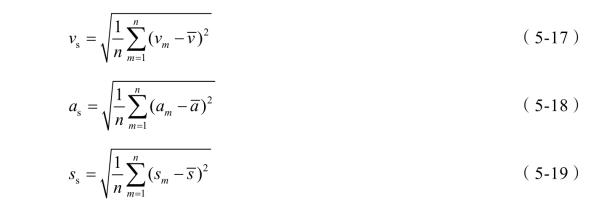
式中，m 表示第m 次样本的状态；n 为在单位时间内采集的样本总量； v m为车辆采集的第m 次车速值； vs 为单位时间内速度标准差； as 为单位时间内加速度标准差； a m表示车辆采集的第m 次加速度值；a 单位时间内加速度的标准差； ss 表示前轮转角标准差； s m为采集的第m 次前轮转角值；s 为单位时间内前轮转角的平均值。

驾驶经验则是通过融合驾驶人的驾龄和驾驶里程得出的，其表达式：

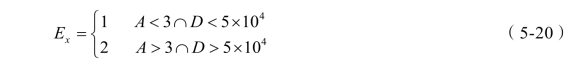
式中，Ex 为驾驶人经验单位为km； A 为驾龄；D 为驾驶里程。

5.4.3.1　基于改进马尔科夫毯（MB-NEW）的属性选择结果

图5-9 所示为采用马尔科夫毯（MB）方法进行人机共驾智能车系统驾驶模式决策属性选择的结果，其中阴影节点为驾驶模式选择的马尔科夫毯。该算法首先获得驾驶模式选择的父子节点集合为车头时距、加速度、车道中心距、驾驶经验、前轮转角标准差，然后寻找选取节点的父子节点，其中加速度的父子节点为X 轴加速度、Y 轴加速度、Z 轴加速度、速度，车道中心距的父子节点为左车道线间距和右车道线间距，前轮转角标准差的父子节点为前轮转角、左转向、右转向，车头时距和驾驶人经验不存在父子节点。由马尔科夫毯的条件独立性及依赖性最后得出车头时距、加速度、车道中心距、驾驶经验、前轮转角标准差、Z 轴加速度、左车道线间距、右车道线间距、左转向、右转向为最终的马尔科夫毯。

为了进一步对人机共驾智能车系统驾驶模式选择决策属性进行优化，最大限度删除冗余属性。本研究对传统的马尔科夫毯算法进行了改进，引入了条件最大条件互信息（CMIM）和边界阈值实现对马尔科夫毯的优化。通过计算得到基于改进马尔科夫毯的属性选择结果如图5-10 所示，最终得出驾驶人经验、车头时距、车道中心距、加速度和车速6 个属性为驾驶模式决策的最优因子集。通过对比分析图5-9 和图5-10 可知，采用改进的马尔科夫毯方法相较于马尔科夫毯方法能够有效地减少选择属性的数量，极大程度上消除了马尔科夫毯中存在的冗余属性。

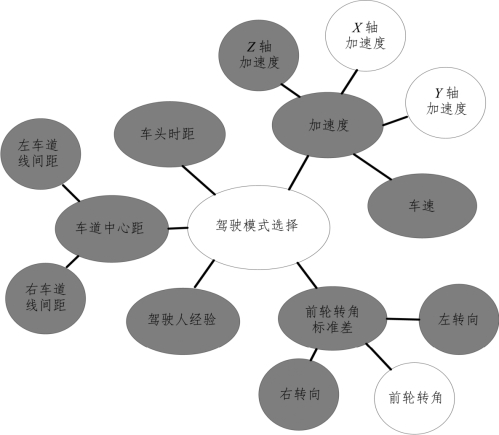
图5-9　基于MB 的属性选择结果

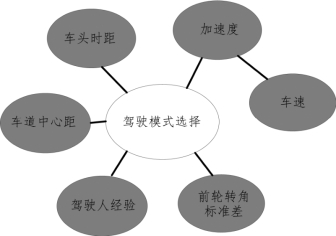
图5-10　基于MB-NEW 的属性选择结果

5.4.3.2　融合信息增益和多分类器的属性选择结果

相关研究表明，当以分类错误率为评价函数时，选择属性的分类准确率最高。所以本研究从分类准确率角度出发提出一种融合信息增益和多分类器的属性选择方法。首先以信息增益为依据对驾驶模式决策属性按照其对驾驶模式影响的重要度进行排序，然后分别采用KNN、SVM 和NB 三个分类器按照排序结果分别选取不同数量的特征进行驾驶模式决策分析。

由于该属性提取方法在进行特征排序时要求所有的决策特征必须为离散型变量，而采集的特征数据多为非离散型变量，所以在进行排序前需将连续变量离散化，本研究采用MDL（最小描述长度方法）[97]对决策变量进行离散化处理，然后通过计算其信息增益来实现对所有属性进行排序。同时，本研究中还采用3 种常用的属性提取方法[以实例（RF）为依据的属性排序方法、贪心选择（Greedy）属性排序法、遗传（GA）最优搜索算法]作为对照进行对比分析。其中以实例为依据的属性排序算法、贪心选择属性排序算法、以信息增益为依据的属性排序算法都是对属性进行排序，而遗传最优搜索算法则是直接选择最优属性集合。不同方法的属性排序和选择结果如图5-11 所示。

由图5-11 可知，采用遗传最优搜索属性选择算法[见图5-11（d）]从20个决策属性中选取前轮转角标准差、驾驶经验、车头时距、车道中心距离为驾驶模式决策因子。而以信息增益为依据的属性排序算法[见图5-11（a）]、以实例为依据的属性排序算法[见图5-11（b）]、贪心选择属性排序算法[见图5-11（c）]分别按照其评价规则对各属性的重要度进行计算并得出排序结果。

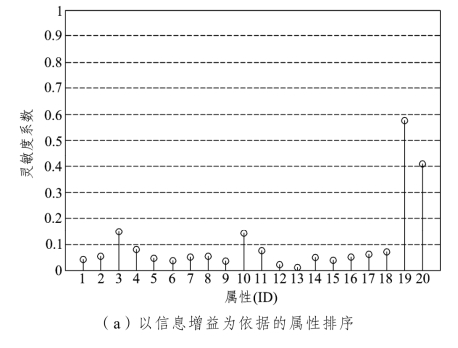
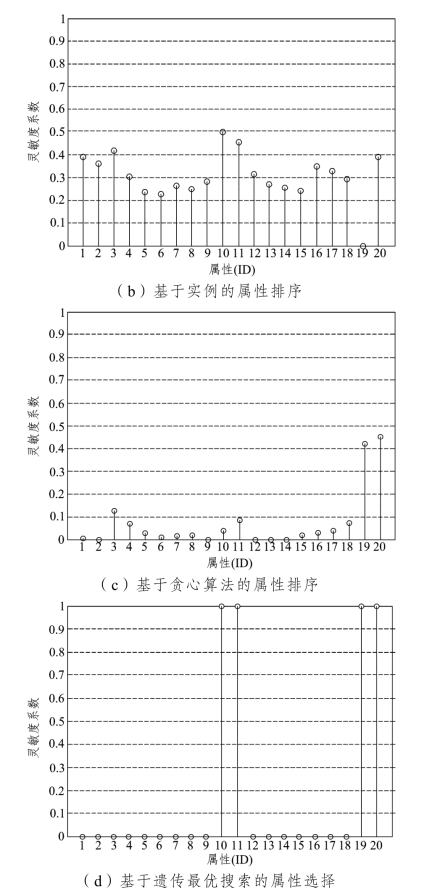
图5-11　不同方法的属性排序和选择结果

（注：图5-11 中X 轴的属性ID 的编号与表5-2 的ID 相对应）

属性排序算法只能实现对驾驶模式决策因子进行排序，无法对最优的提取结果进行确定。而加入分级模型则能够有效解决这一问题。通过对选择不同数量属性计算其分级准确率，最后选择最优属性组合以期得到最优识别结果。本研究中采用SVM、NB、KNN 这3 种常用的分类器模型对不同属性选择方法下的识别效果进行评价。在测试过程中，将所有的数据集分成10 份，轮流将其中9 份作为训练集，剩余1 份作为测试集，10 次结果的均值则为对算法精度的估计。图5-12～5-14 所示为不同分类器采用不同属性提取算法时的分类结果。

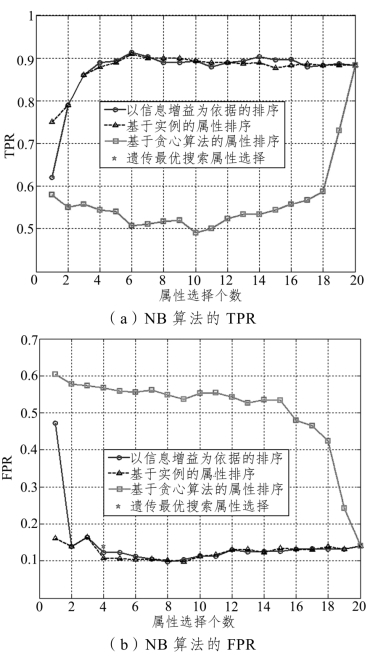
图5-12　不同属性选择算法下NB 的分类结果

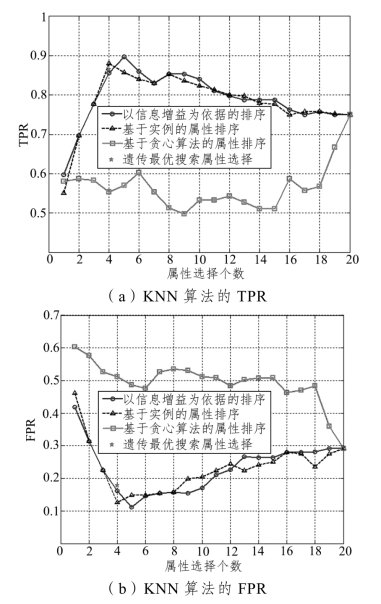
图5-13　不同属性选择算法下KNN 的分类结果

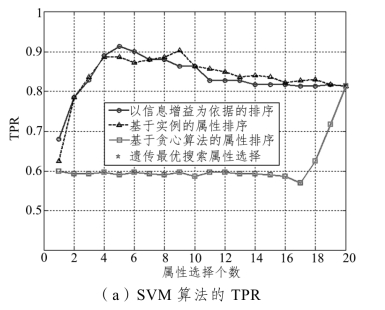
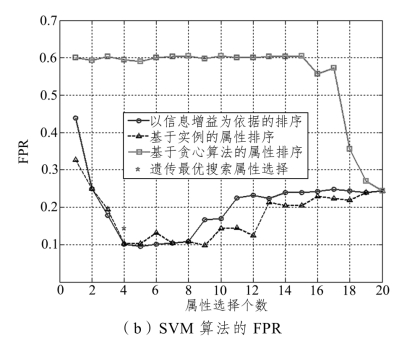
图5-14　不同属性选择算法下SVM 的分类结果(www.xing528.com)

由图5-12 可知，当采用NB 作为分类器时，以信息增益为依据的属性排序算法选择前6 个属性为决策因子时，分类的TPR 和FPR 结果最为理想。基于实例排序算法的分类最优结果也是出现在选择前6 个属性时。而贪心算法的最优分类结果则为选择所有属性时出现。

由图5-13 可知，当采用KNN 作为分类器时，以信息增益为依据的属性排序算法选择前5 个属性为决策因子时，分类的TPR 和FPR 结果最为理想。基于实例排序算法的分类最优结果出现在选择前4 个属性时。而贪心算法的最优分类结果则为选择所有属性时出现。

由图5-14 可知，当采用SVM 作为分类器时，以信息增益为依据的属性排序算法选择前5 个属性为决策因子时，分类的TPR 和FPR 结果最为理想。基于实例排序算法的分类最优结果出现在选择前9 个属性时。而贪心算法的最优分类结果则为选择所有属性时出现。

此外，由于遗传最优搜索算法不具有参数可调性，所以其在图中的结果只有一个点，即其最优分类结果在选择4 个属性时出现。

由上可知，当采用不同的分类算法和属性选择方法进行计算时，所选取的最优属性集合也具有一定的差异性。为了能够获取最佳的属性结合，需对不同属性选择方法和分类算法组合下的分类结果进行分析。其对比分析结果如图5-15 所示。

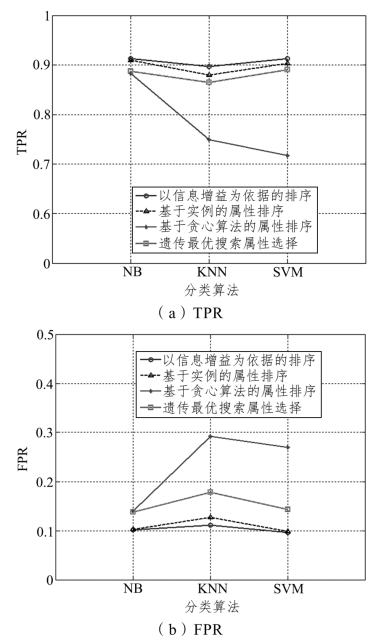
图5-15　不同属性选择方法和分类算法组合的最优分类结果

由图5-15 可知，采用以信息增益为依据的属性排序方法后，进行分类辨识得到的分类真正率（TPR）[见图5-15（a）]相较于其他三种算法更为优越，同时分类假正率（FPR）[见图5-15（b）]也较小。当采用以信息增益为依据的属性排序方法和支持向量机或朴素贝叶斯组合进行识别时真正率最大为0.913，此时假正率分别为0.102 和0.096。其选择的属性数量分别为5 个和6个。所以可以认为选择5 个或者6 个属性进行识别时都能得到理想的分类结果。其中5 个属性的集合为车速、车头时距、加速度、前轮转角标准差、驾驶经验，而6 个属性的集合为车速、车头时距、加速度、前轮转角标准差、驾驶经验和车道中心距。

5.4.3.3　改进马尔科夫毯（MB-NEW）算法执行效率验证

由于人机共驾智能车系统驾驶模式决策实验为探索性研究，所以采集的数据样本有限，不同属性选择算法的执行效率差异性较小。为了验证本研究提出的改进马尔科夫毯方法在属性选择执行效率方面的优越性，实验选择美国FARS（Fatality Analysis Reporting System，死亡事故分析报告系统）中2010—2014 年的事故数据开展测试，并将数据按照年份分为不同的6 个数据集。通过对原始数据进行预处理，对无效和不可量化的数据进行消除，最终得到的数据集如表5-3 所示。

表5-3　FARS 数据集

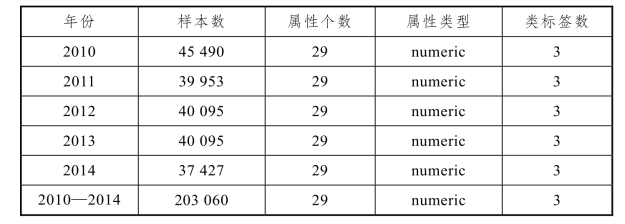
表5-3 中，根据事故的严重程度将类标签分为没有伤亡、有伤亡、存在严重伤亡这3 种，而数据集中属性的特性则如表5-4 所示。

表5-4　FARS 数据属性描述

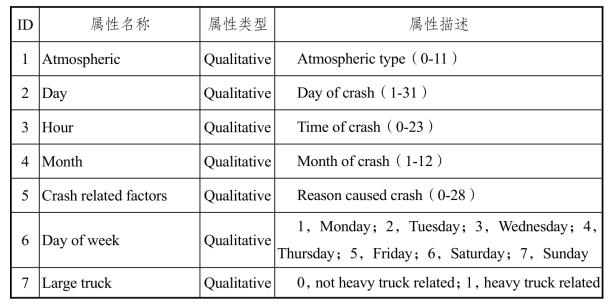
续表

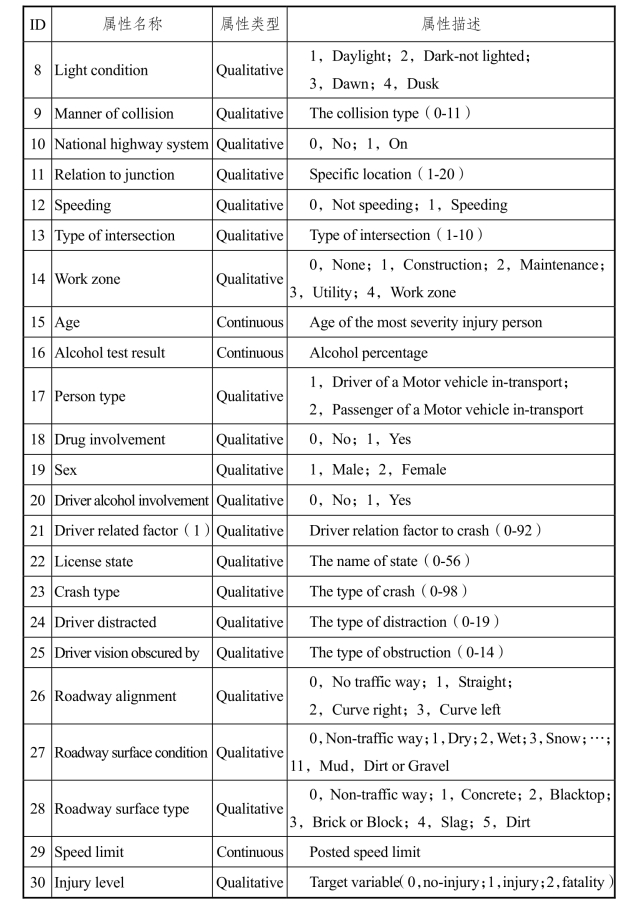
从表5-4 中可以看出，考虑到各个属性的特点，对其属性状态分类也存在较大的差异性。数据集中的数据类型包括定性的属性，同时也包含了定量的变量。为了能够实现对这些异质数据的分析，在实验之前采用有监督离散算法Minimum Descriptive Length（MDL）对其进行离散化，然后再进行相应的计算处理。

为了综合分析改进马尔科夫毯方法在处理大样本数据集上的优势，本研究将所提出算法（MB-NEW）与现有的应用较为广泛的特征选择算法[FCBF、ReliefF 及嵌入机器学习算法（SVM）的属性排序方法（Wrapper-SVM）]进行比较，以下为3 种典型算法的简单介绍。

FCBF（Fast Correlation-Based Feature selection）[98]：在这个算法中，度量准则为Symmetrical Uncertainty（SU）。首先按照特征的相关性降序排列所有的特征，然后再是近似马尔科夫毯排除冗余特征，其准则是：如果SU ( F1 ; C )＞SU ( F2 : C)且SU ( F1 ; C )＞SU ( F1 ; F2)，那么就是的冗余特征。

ReliefF[99]：是一个著名的基于距离的特征排序方法。该方法选择特征的准则是选择具有最大区分不同类标签距离和最小区分相同类标签距离的特征。该算法在运行前需要设定近邻数k 和参与样本数m，根据文献，本研究中k 取5，m 取30。

Wrapper-SVM：该方法的特点就是将支持向量机算法嵌入Wrapper 类属性排序算法中，以分类准确率为评价依据得出最优或者局部最优属性集合。

而考虑到这3 种算法在Weka 平台中已经存在，所以本研究直接调用这些算法进行运算。不同算法在不同数据集中属性选择的结果和运行时间如图5-16 和表5-5 所示。

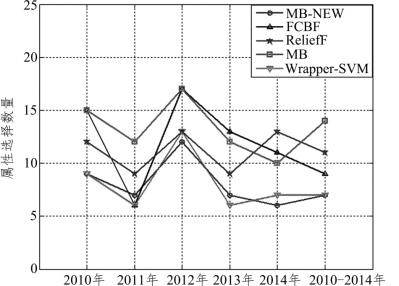
图5-16　各算法属性选择结果

表5-5　各属性选择算法执行时间

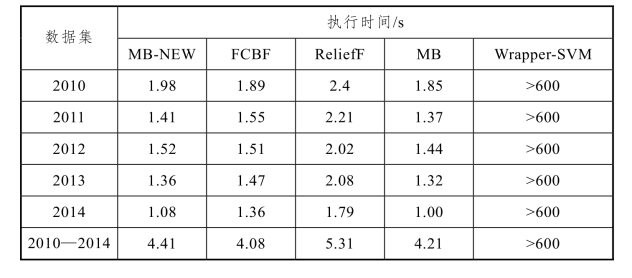
由图5-16 可知，采用MB-NEW 和Wrapper-SVM 对交通事故严重性关联属性进行选择时，其选择的属性数量相较于其他算法最少。而从算法的执行时间可以看出，MB 算法的执行时间最短，MB-NEW 次之。此外，为验证属性选择结果对交通事故严重性识别的影响，采用前文提到的 3 种分类器（KNN、NB、SVM）分别进行分类识别，得到不同属性选择算法的识别准确性对比结果，如图5-17 所示。

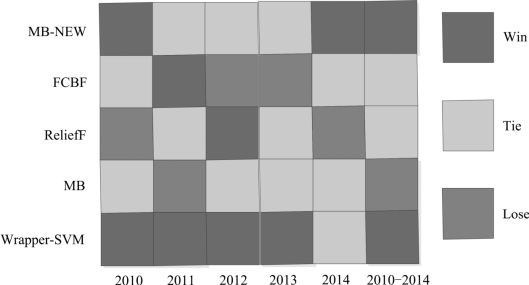
图5-17　不同属性选择算法的识别准确性对比

由图5-17 可知：MB-NEW 算法在3 个数据集中分类结果为最优，而Wrapper-SVM 算法则在5 个数据集中最优，FCBF、和ReliefF 分别出现过一次分类结果最优。由此可知，就分类准确性而言，采用Wrapper-SVM 属性选择效果最佳，MB-NEW 算法次之，其余3 个算法各有优劣。

通过对不同属性选择算法的属性选择数量、算法执行时间、分类准确率三方面结果进行分析可知：MB-NEW 算法在属性选择数量、算法执行时间、分类准确率都体现出较大的优越性，虽然Wrapper-SVM 算法在分类准确率方面要优于 MB-NEW 算法，但是 MB-NEW 算法执行效率要远远高于Wrapper-SVM 算法。当数据维度较高或者样本数量庞大时，采用MB-NEW算法进行属性选择显然更好。