改进的MB-NEW方法：智能车辆行为决策与安全评估

作为一种典型的Filter 属性选择方法，马尔科夫毯（Markov Blanket）方法的优势是能够对多维高样本量的数据进行属性提取，通过消除和约减冗余变量的方法进行属性选择，其评价函数是属性与目标属性之间的相关性测度[87]。

1996 年，Koller 等人率先提出将马尔科夫毯方法引入工程应用领域，并很快在该领域得到了广泛的应用。其定义为：假设存在一个数据集V，其目标变量为T ，则目标变量T 的马尔科夫毯可以定义为MB (T　)（数学表述见定义1）。其中MB (T　)为目标变量T 的最优属性集，MB (T　)中所有的子属性 f i与目标变量之间的关系都是独立的（独立性判断见定义2）。由此可知，根据MB (T　)中变量状态即足以确定目标变量T 的概率分布，而不需要利用所有属性进行选择预测。更重要的是，在一定条件下（满足贝叶斯网络的忠实性条件见定义3），M B (T　)在贝叶斯网络（见图5-4，其中阴影部分为目标变量T 的马尔科夫毯）中是一个包含目标变量T 的父节点、子节点以及子节点的父节点的属性集合[88]。

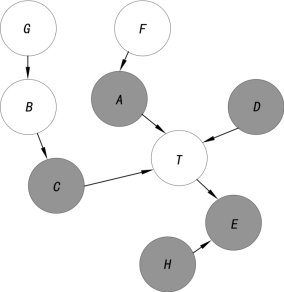
图5-4　贝叶斯网络中的马尔科夫毯（示例）

定义1（马尔科夫毯）：假设存在目标属性T ∈V ，则目标变量T 的马尔科夫毯为MB (T　)，MB (T　)应满足：

式中，V 为属性全集；标志“⊥”表示独立性。

定义 2（条件独立性）：给定一个目标属性f i，假设属性子集Mi ⊂F(f i∉Mi)，我们称M i是 f i的马尔科夫毯，当且仅当在给定M i的条件下 f i与F -Mi-{ fi}是独立的，则有：

推论1：假设属性子集M i是属性 f i的马尔科夫毯，那么在给定M i的条件下， fi 与类C 之间的关系也是独立的：

由定义2 和推论1 可知，所选择的马尔科夫毯必然不包含无关属性，当一个属性完全依赖于另一属性时，可以将该属性看作是另一个属性的冗余，进而实现对冗余属性的删减。

定义3（忠实性，faithfulness）：存在无环图G（见图5-4）忠诚于变量集合T 的联合概率分布P，当且仅当P 的每个独立分布都是由无环图G 及其马尔科夫条件所决定。一个分布P 是忠诚的当且仅当存在这样一个有向无环图G，且G 忠诚于P。在忠实性贝叶斯网络中，任意变量的马尔科夫毯都是唯一存在的。

根据马尔科夫毯的定义及其特点可得出，其实现流程可以分为以下5 个步骤：

（1）输入各个属性和类属性的样本数据，并对数据进行归一化处理；

（2）采用启发式搜索方法寻找与目标类属性相关的变量；

（3）利用独立性条件对错误或无关节点进行去除，获取目标类属性的父子节点集合；

（4）根据条件依赖性从获取集合的父子节点中得出目标类属性的配偶节点；

（5）输出最终得出的目标类属性的马尔科夫毯。

基于马尔科夫毯的属性选择方法的伪代码如算法5-1 所示。算法中以属性子集F 和类T 为输入，以类T 的马尔科夫毯MB (T ) 作为算法的输出。其中算法主要包括两个步骤：第一步（算法中第2～6 行）将属性节点添加到MB (T )中，该步骤中采用的搜索算法是启发式搜索（算法中第3 行），在这一过程中，其中可能存在部分不属于MB (T　)的属性节点也同样会被添加到MB (T　)中，而这些无关的节点将通过第二步（算法中第7～9 行）进行删除[89]。(www.xing528.com)

在该算法中，数学符号“⊥/ ”表示“不独立于”，“⊥”表示“独立于”，“|”表示“在满足某条件下”，“dep”表示“满足独立性条件”。

算法5-1：基于马尔科夫毯的属性选择算法（MB）。

在马尔科夫毯算法中，属性与类之间的独立性主要依靠两变量之间的互信息决定的。其中互信息的定义如下：

在随机变量Y 的取值条件确定的条件下，随机变量X 的条件熵 H ( X | Y)小于或者等于变量X 的无条件熵 H ( X )其计算公式：

当Y 已知时，X 的不确定度减少量为 H ( X )-H ( X | Y)，该差值即为随机变量X 和Y 之间的互信息 I ( X ; Y )，其计算方法：

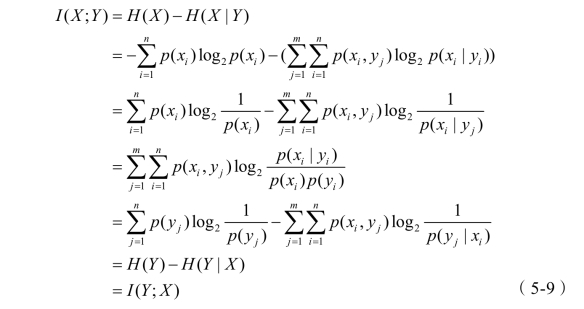
式中， xi 为属性集合中的某一属性，其对应的概率分布为 p ( xi )； yi 为目标类属性集合中的某一属性，其对应的概率分布为 p ( yi )。

由式 5-9 可知，互信息 I ( X ; Y )与 I ( X ; Y )是相等的，且都满足关系式0≤I ( X ; Y)=I (Y　; X) ≤min( H ( X )， H (Y　))，当变量X 与Y 之间统计独立时有I ( X ; Y ) = 0。在马尔科夫毯算法中，类的值一般都是已知的，通过计算属性与类之间的独立性即可确定类的马尔科夫毯。

相关研究表明，采用马尔科夫毯属性选择方法能够去掉数据集中的无关和冗余属性，并最终得到一个最优的属性子集。采用马尔科夫毯属性选择方法需对所有属性子空间进行搜索，其计算复杂性很高，时间复杂性达到O（2n），当属性维数较高或者样本数量过大时，计算其马尔科夫毯几乎是无法实现的。因此，本研究中拟引入最大条件互信息（CMIM）和边界阈值ε 分别从属性冗余性和计算收敛速度两方面对马尔科夫毯方法进行改进和提高。

在广义信息论中，条件互信息的作用就是用来表明在某个随机变量的数值条件已知的条件，其余随机变量之间存在的相互关系。由此可得出其定义为：当随机变量T 的一个值t 已知时，随机变量X 和Y 之间的互信息可由式（5-10）计算得出。

另外，根据条件互信息的定义及式（5-10）可得出：

通过采用关系式（5-11）即可计算条件熵已知条件下变量之间的条件互信息。在属性选择过程中，T 为类别， X 为不包含于MB (T　)中的属性，Y 可表示为MB (T　)， I ( X ; Y | T )表示属性Y 已经确定的前提下，属性X 所包含的与类别相关的信息。此外，为了避免由于样本数量或变量维度过高导致的无法找到马尔科夫毯的现象，书中引入边界阈值ε 进行边界设定，当条件互信息值 I ( X ; T |MB (T ))＜ ε时，我们认为X ⊥T |MB (T　)。

算法5-2：改进的马尔科夫毯算法（MB-NEW）。

在算法5-2 中，改进的马尔科夫毯算法（MB-NEW）包含两个阶段：生长阶段（算法5-2 中第2～9 行）和收缩阶段（算法5-2 中第10～14 行）。生长阶段的任务是保证能够找到马尔科夫边界，并且在这个边界之外其他属性对类T 而言都是多余的。而在收缩阶段，改进的马尔科夫毯算法通过采用条件互相关性进一步删除冗余的属性。同时，通过参考前人研究成果[90]最终将边界阈值ε 设定为0.01。算法中，互信息用 I (· | )· 表示，值得注意的是，条件属性集合在每一步迭代过程中都会发生变化，直到得出最优或局部最优马尔科夫毯算法终止。