K-means聚类算法介绍及其应用

假设存在样本数据集为S={x1 ， x2， …， xn}，需将该数据集通过采用K-means 聚类算法自动划分为K 类，其中每个类分别用 C1 ， C2， …， CK表示，则C1 ， C2， …， CK应满足：

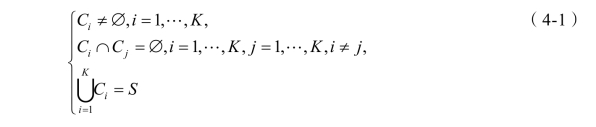
目前，聚类结果类别的判定最常用的方法为多维欧式距离法，其评价的准则函数J 如式（4-2）：

其中， ni 表示第i 个簇的对象个数； d ij( x j， C i)表示各个簇中所有数据对象到其对应的簇质心的欧式距离。由此可知，准则函数J 表示为所有对象对其所在簇中心的欧式距离之和，当函数J 的值越小时，说明簇内各对象之间关系越紧凑，与其他不同簇之前就越独立。所以通过不断对函数J 的取值进行优化最终能够获取最优的聚类方案[73]。

采用K-means 聚类算法对驾驶行为险态进行辨识分类的具体步骤如下：

（1）确定用于聚类分析的特征向量 xi 及其数据集S={x1 ， x2， …， xn}。

（2）确定聚类数目，根据数据特点将聚类数目设定为C = 3（将驾驶行为险态分为可忽略、可容忍、不可容忍三类）。

（3）从数据集S 中随机选取3 个为初始聚类中心 C1 ， C 2，C 3。(www.xing528.com)

（4）计算各数据对象到设定的初始聚类中心的欧式距离 d [ xi ， C j( I )]，其中i=1，2， …， n ，I=1，2，3，若满足 d [ xi ， C j( I)] =min{d　[ xi ， C j( I )]，j=1，2，3}，则xi = Cj；

（5）重新寻找簇的质心 Ci ( I+1)，I=1，2，3，其计算公式：

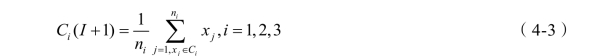
（6）当存在任意的 i ∈{1，2，3}，对于 Ci　( I+ 1)=C i( I )都成立时，算法终止。且当前的 Ci ( I )，I =1，2，3为最终的簇，否则，返回步骤（4）。值得注意的是，为了避免由于无法得出最优解而导致的无限循环，算法中设置最大的迭代次数为10，当运行至最大迭代次数时，算法也将终止，并输出最终的聚类结果。

（7）对输出的聚类结果进行判断，通过调整迭代步数等再次优化聚类结果[74]。

该算法实现的流程如图4-9 所示。

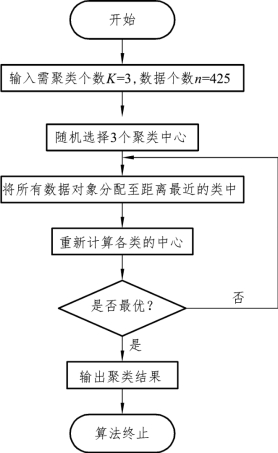
图4-9　K-means 聚类算法流程