生态建筑第三版：多层次权重分析法

多层次权重分析法又称为AHP（the analytical hierarchy process），该分析法是美国著名数学家T.L.Saaty于20世纪70年代初提出的用于分析复杂问题的一种方法。其原理是把要研究的复杂问题看作一个大系统，通过对系统的多个因素的分析，划分出各因素相互联系的有序层次，再请专家对每一层次各因素进行判断后，给出相对重要性的定量表示，通过建立或利用相关数学模型，计算出每一层次全部因子的权重并排序；最后通过排序结果进行分析决策。这种方法是把人的思维过程层次化、数量化，用数学分析为决策提供较为客观的依据，实质是一种定性与定量相结合的分析方法。新疆塔里木河中下游面临严重的生态危机，生态环境恶化已严重阻碍了当地经济发展，退耕还林、还草是其恢复生态的重要措施。对其退耕进行适宜性分析，可为其退耕规划和退耕规模提供相关依据。结合新疆塔里木河中下游退耕适宜性分析的实例，将多层次权重分析法的实施步骤说明如下。

（1）分析系统中各因素之间的关系，建立系统的递阶层次关系（见图3-10）。其中，最高层也称为目标层，是问题的预定目标或理想状态；中间层是实现目标所涉及的中间环节考虑的准则，它可由若干准则和子准则组成；最底层指实现目标可供选择的各种措施、决策和方案，也是具体的影响因素。

（2）构造两两比较判断矩阵。当某层元素ui对上一层元素的重要性可以定量时（如货币、重量、质量等），其权重就可以直接确定；当不能定量只能定性时，就要用两两比较方法，确定各元素的重要程度。两两比较时，一般按1～9比例标度对重要性程度进行赋值，表3-5示出了各数值的标度含义。

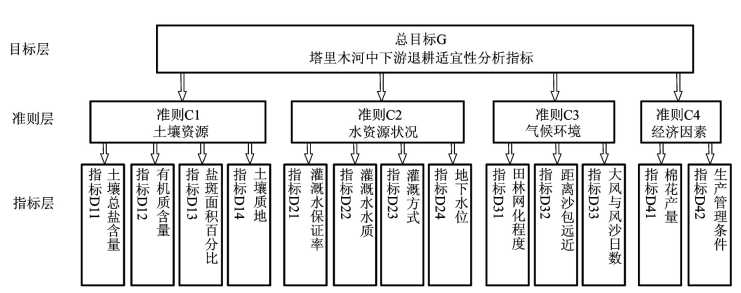
图3-10　塔里木河中下游退耕层次分析结构图

（来源：编者根据文献［45］整理）

表3-5　标度的含义

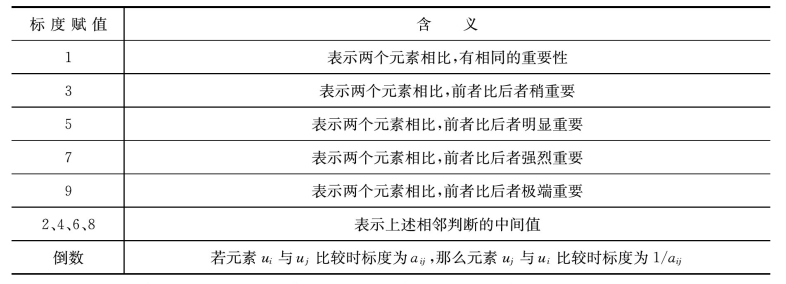
根据n个元素两两比较标度赋值aij，可以创建一个n阶判断矩阵A=（aij）n×n。由于有aij＞0、aii=1、aji=1/aij三种情况，判断矩阵A只要知道上三角或下三角各元素即可，也就是只需作n（n-1）/2次判断即可创建判断矩阵。对塔里木河中下游退耕适宜性分析建立的判断矩阵如下：

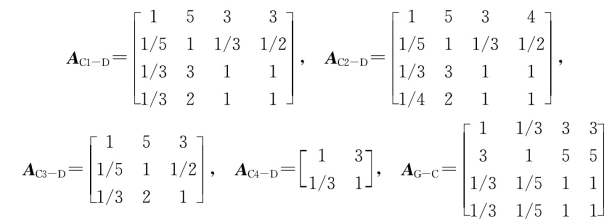
（3）元素对上层指标的影响权重计算。元素ui对上层指标的影响权重ωi的计算主要有下列三种方法。

第一种方法称为和法，就是将判断矩阵A的n个行向量归一化后取算术平均值，作为权重值，即按式（3-1）进行计算。

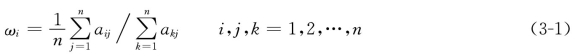
第二种方法称为根法，就是将A的各行向量进行几何平均，然后归一化处理得到的行向量即为权重向量，即按式（3-2）进行计算。

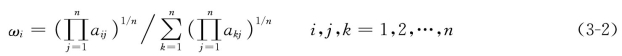(www.xing528.com)

第三种方法称为特征根法，就是求解矩阵A的n个特征根，即解方程|A-λE|=0，利用最大的特征根值λmax按AW=λmaxW求出对应的特征向量W（W1，W2，…，Wn），然后将W进行归一化处理得到ωi，也就是按式（3-3）计算ωi。

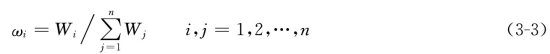
对塔里木河中下游退耕适宜性进行分析，利用特征根法计算各元素对上层指标的影响权重，见表3-6。

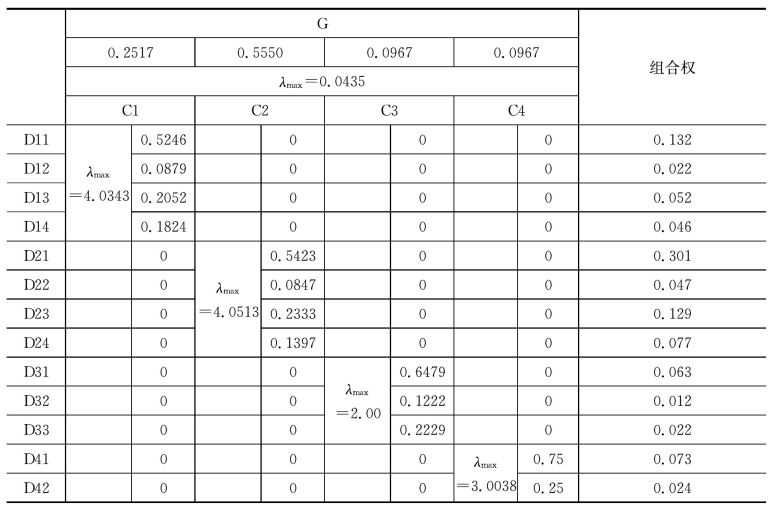
表3-6　各层级判断矩阵最大特征值及各层元素权重值

采用这种方法需要进行一致性验证。首先按照式（3-4）计算一致性指标CI（consistency index），然后按照表3-7查出对应的平均随机一致性指标RI（random index），最后按照式（3-5）计算一致性比例CR（consistency ratio）。当CR＜0.1时，认为一致性是可以接受的，当CR≥0.1时，应该对判断矩阵进行适当修正。

表3-7　平均随机一致性指标RI

（4）计算各层元素对目标层的总排序权重值。总排序权重值的计算是自上而下地将单准则下的权重进行合成，并逐层进行一致性检验。设k-1层上有m个元素，它们对总目标的排序权重向量为k层上有n个元素，它们对k-1层上第i个准则的排序权重向量为在中，当j元素不受i准则支配时，权重值赋0，这样可以构造k层元素对k-1层所有准则的权重向量矩阵它是一个m×n阶矩阵。最后，按照式（3-6）计算k层上元素对目标层的排序权重向量Wk。逐层下推，即可得到最底层各元素对目标层的排序权重值。

设k-1层上元素i为准则的一致性指标为平均随机一致性指标为一致性比例为按照式（3-7）和式（3-8）从上到下分别进行各层一致性验证。

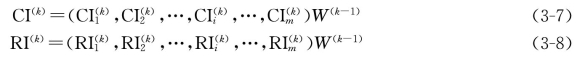
表3-6中最后一列示出了所选因素对塔里木河中下游生态环境的影响权重。从适宜性分析的结果可以看出，灌水保证率是最重要的因素，其次是土壤总盐含量，再次是灌溉方式。