建筑识图与房屋构造：圆和曲面立体的轴测投影

1）正等测投影

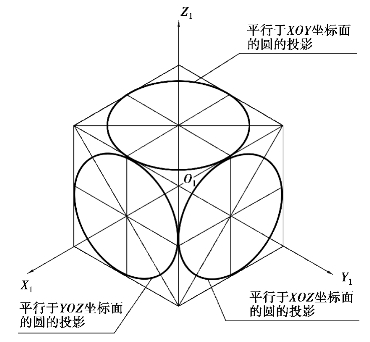
图5.15　圆的正等测投影

（1）圆的正等测投影

在平行投影中，当圆所在的平面平行于投影面时，其投影是圆；当圆所在的平面平行投射方向时，其投影为直线；而当圆所在平面倾斜于投影面时，则投影为椭圆。如图5.15所示为三个坐标面内直径相等的圆的正等测投影。

工程上常用近似画法来作轴测椭圆，对于平行于坐标面的圆的正等测投影，通常采用“四心法”近似画椭圆。“四心法”画椭圆就是用四段圆弧代替椭圆。下面以平行于H面（即XOY坐标面）的圆，说明圆的正等测图的画法，如图5.16所示。

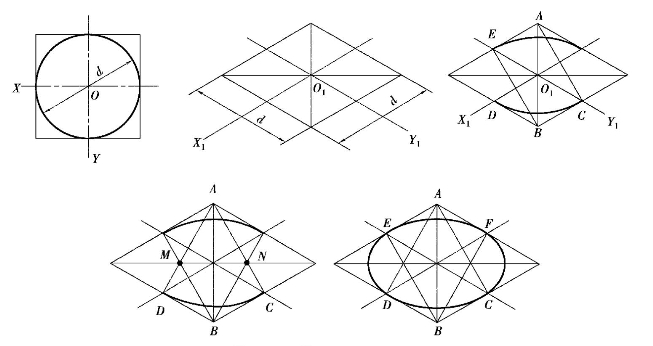
图5.16　用四心法画椭圆

作图步骤如下：

a.画出轴测轴，按圆的外切正方形画出菱形。

b.以A，B为圆心，AC，BE为半径画两大弧。

c.连AC和AD分别交长轴于M，N两点。

d.以M，N为圆心，MD，NC为半径画两小弧，在C，D，E，F处与大弧连接。

（2）曲面立体的正等测投影

掌握了圆的正等测的画法以后，就不难画出曲面立体的正等测投影。图5.17（a）及图5.17（b）所示分别为圆柱和圆台的正等测画法，作图时先分别用四心法作出其顶面和底面的椭圆，再作其公切线，擦去多余线型并描深加粗即成。

（3）圆角的正等测投影

圆角正等测投影的作图过程如图5.18所示。

作图步骤如下：

①在角上分别沿轴向取一段长度等于半径R的线段，得A，A′和B，B′点，过这4点作相应边的垂线分别交于O1及O2。

②以O1及O2为圆心，以O1A及O2B为半径作弧，即为顶面上圆角的轴测图。

③将O1及O2点垂直下移，取O3，O4点，使O1O3=O2O4=h（板厚）。以O3及O4为圆心，以O1A及O2B为半径作弧，作底面上圆角的轴测图，再作上、下圆弧的公切线，即完成作图。

④擦去多余的图线并描深，即得到圆角的正等测图。

【例5.10】试画出图示形体的正等测图。

【解】作图过程如图5.19所示。

2）斜二测投影

（1）圆的斜二测投影

在斜二测中，三个坐标面（或其平行面）上圆的轴测投影如图5.20所示。(www.xing528.com)

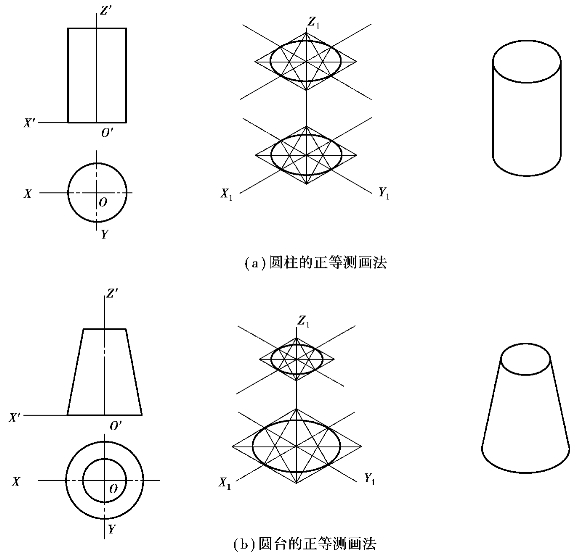
图5.17　曲面立体正等测投影

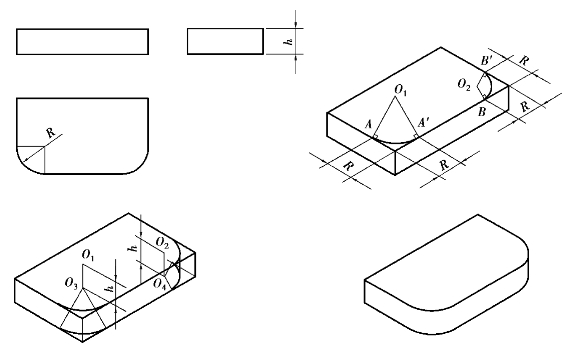
图5.18　圆角的正等测投影

斜二测投影中的椭圆不能用四心法绘制，所以现在再介绍一种画椭圆的方法——“八点法”，这种方法不仅适用于斜轴测投影，也适用于正轴测投影中。

下面以平行于H面（即XOY坐标面）的圆，说明圆的斜二测图的画法，如图5.21所示。

作图步骤如下：

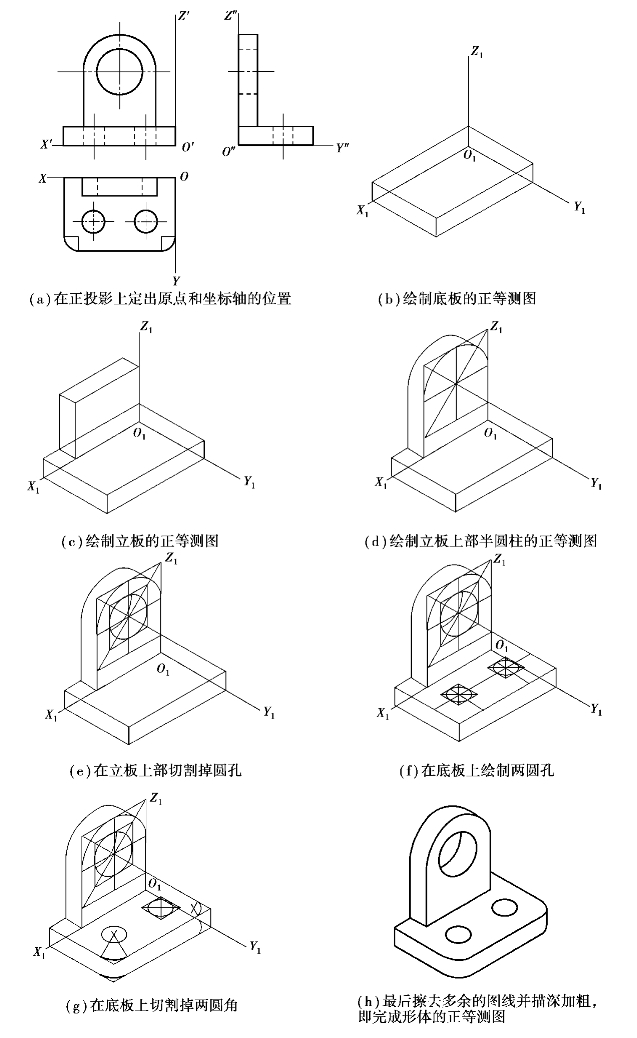
图5.19　综合法绘制形体的正等测图

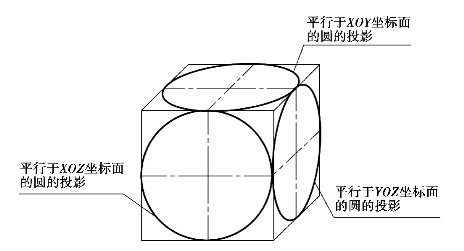
图5.20　圆的斜二测投影

①在圆的正投影图中作圆的外切正方形ABCD及对角线AC，BD，则正方形和对角线分别和圆相交于8个点，如图5.21（a）所示。其中1，2，3，4为正方形各边的切点；5，6，7，8为对角线上的点。

②如图5.21（b）所示，作圆的外切正方形及其对角线的斜二测投影，则此四边形与O1X1，O1Y1的交点即为4个切点的轴测投影——11，21，31，41。

③任取四边形的一个边C1D1，在其上以C141为底边，作一个等腰直角三角形C1E141，然后再以其腰长41E1为半径画圆弧则可在边C1D1上截得M1，N1两个点。过M1，N1点引O1Y1轴平行线，与四边形对角线A1C1及B1D1分别交得51，61，71，81各点，即5，6，7，8各点的轴测投影，如图5.21（b）所示。

④将11—81各点用光滑曲线相连，然后加深即可完成平行于H面圆的斜二测，如图5.21（b）所示。

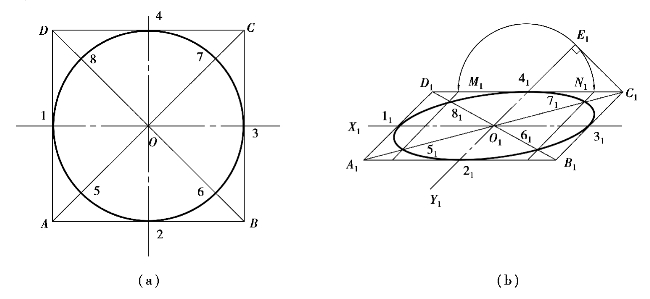
图5.21　八点法画椭圆

（2）曲面立体的斜二测投影

作出带孔圆台的斜二测投影，如图5.22所示。

作图方法与步骤如下：

①建立轴测轴O1X1，O1Y1，O1Z1，在O1Y1轴上量取L/2，定出前端面的圆心A。

②作出前、后端面的轴测投影。

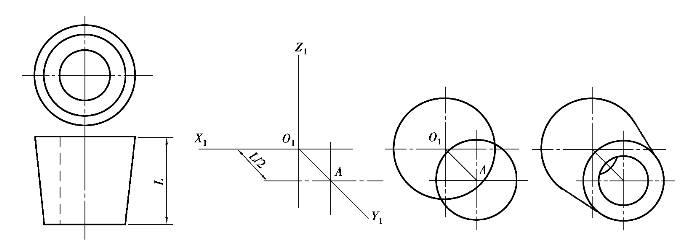
图5.22　带孔圆台的斜二测投影

③作出两端面圆的公切线及前孔口和后孔口的可见部分。

④擦去多余的图线并描深加粗，即得到圆台的斜二等轴测图。