常用的平面立体轴测投影画法

1）正等测投影

当选定三个轴向变形系数相等时，即p=q=r，所得的正轴测投影称为正等测投影。经过计算，可得p=q=r=0.82，φ=σ=30°，轴间角均为120°，如图5.2所示。但在实际作图中，按上述的轴向伸缩系数计算尺寸是相当麻烦的。由于绘制轴测图的主要目的是表达物体的直观形状，因此为了作图方便，常采用简化轴向变形系数，取p=q=r=1，即平行于轴向的所有线段都按原长度量，这样画出来的轴测图沿轴向分别放大了1/0.82≈1.22倍，如图5.3所示为长方体分别用未简化和简化的轴向变形系数所作的对比，由图可见其形状是不变的，仅是图形按一定比例放大。

图5.2　正等测的轴间角及轴向变化率

①坐标法：即将形体上各点的直角坐标位置移植于轴测坐标系统中去，定出各点的轴测投影，从而就能作出整个形体的轴测图。

【例5.1】试用坐标法画出图示正六棱柱的正等轴测图。

【解】由于形体的轴测图习惯上是不画出虚线的，因此作正六棱柱的轴测时，为了减少不必要的作图线，先从顶面开始作图比较方便。作图过程如图5.4所示。

【讨论】例题5.1所选用的是Z轴向下方，作图时也可选择Z轴向上，但是后期作完图后，擦拭图纸上其余线形时，擦拭的线形相对多一点，所以本题在讲解实例时选取的是Z轴向下的方向，读者可自行比较，体会轴测图绘制的灵活性。

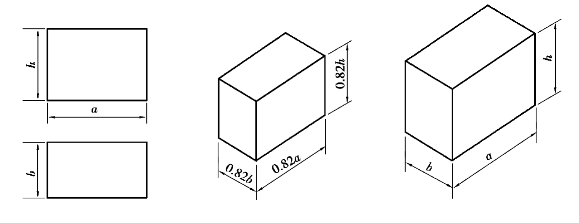
图5.3　长方体的正等测

图5.4　正六棱柱正等测的作图步骤（坐标法）

由此题读者可自行思考棱柱的绘制，例如三棱柱、四棱柱等。

【例5.2】试画出图示棱台的正等轴测图。

作图过程如图5.5所示。读者绘制轴测图的过程中可以将坐标轴及其原点的位置自己选定在其他的方位。

图5.5　棱台的正等测的作图步骤

【例5.3】试画出图示棱锥的正等轴测图。

【解】棱锥的轴测绘制，选择中心点为坐标点原点绘图会相对简单一些，作图过程如图5.6所示。

【讨论】读者可自行思考其余棱锥的绘制，例如正三棱锥、正四棱锥及其正五棱锥的绘制，由此掌握棱锥的基本绘制方法。

②切割法：是将切割型的形体，看作一个完整的、简单的基本形体，作出它的轴测图，然后将多余的部分逐步地切割掉，最后得到形体的轴测图。

【例5.4】试用切割法画出图示正六棱柱的正等轴测图。

【解】例题5.1的六棱柱的绘制采用了坐标法绘制，此处题目要求用切割法绘制，那么就要将原切割前的形体先绘制出来，再进行切割。此处可假设六棱柱原来是一个四棱柱，那么切去四棱柱的4个角即可得到六棱柱。作图过程如图5.7所示。

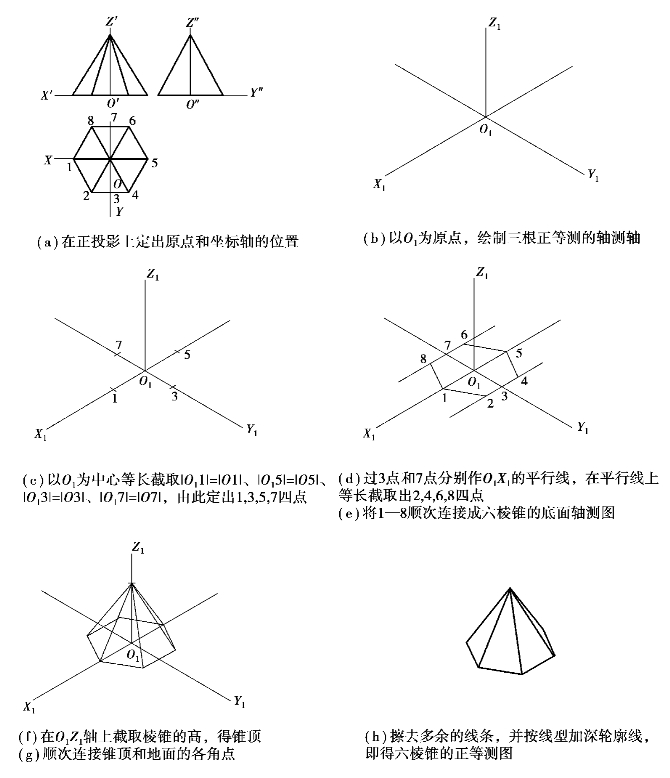
图5.6　棱锥的正等测的作图步骤

【例5.5】试用切割法画出图示形体的正等轴测图。

【解】观察形体，得出形体的最初状态是一个四棱柱，然后在四棱柱上又切割了一个三棱柱，再在剩下的形体上切割掉一个楔块，由此知此形体是在四棱柱的基础上，切割了两次而得出的，分析过程如图5.8所示，作图过程如图5.9所示。

③叠加法：将组合体的轴测投影分为几个部分，然后分别画出各部分的轴测投影，从而得到整个形体的轴测投影。画图时注意叠加时的相对位置的确定。(www.xing528.com)

【例5.6】试用叠加法画出图示形体的正等轴测图。

【解】运用叠加法作图过程如图5.10所示。

④综合法：对于较复杂的组合体，可先分析其组合特征，然后综合运用其他的绘制方法画出其轴测投影（见例5.7和例5.10）。

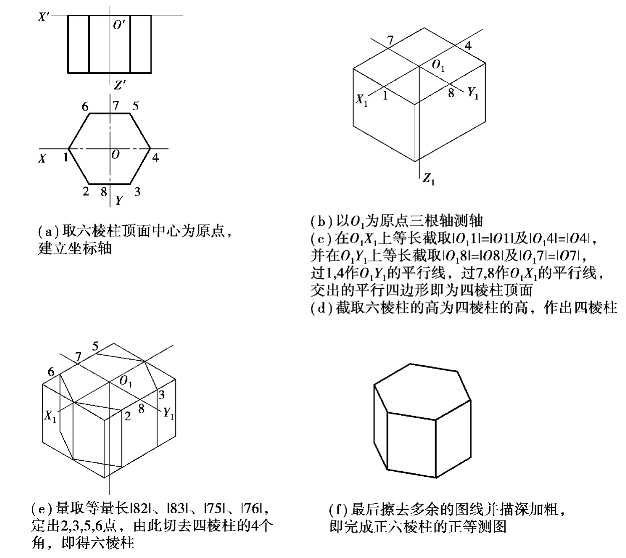
图5.7　正六棱柱的正等测的作图步骤（切割法）

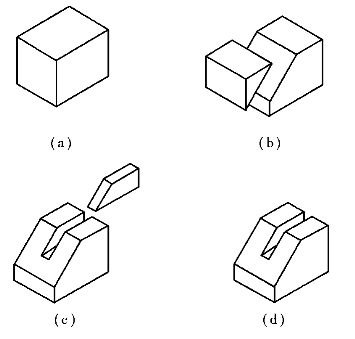
图5.8　切割法绘制形体的分析形成过程图示

读者可不拘泥于以上的几种作图方法，只要能准确和迅速地画出形体的轴测即可，从而归纳和总结自己的绘制方法。

【例5.7】根据三视图画出图示形体的正等轴测图。

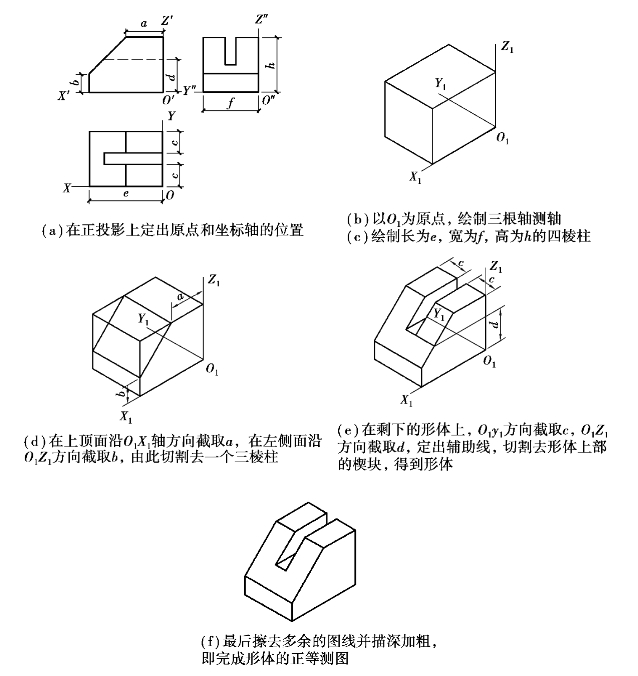
图5.9　切割法绘制轴测形体的作图步骤

【解】先将各部分基本形体绘制出来，根据相对位置组合在一起，然后对基本形体进行切割，最后擦去多余图线，加粗形体线，如图5.11所示。

2）斜二测投影

当形体仍处于正投影的位置，投射方向倾斜于投影面，将形体向投影面投影，所得的投影称为正面斜二测投影（斜二测）。如图5.12所示，其轴间角∠X1O1Z1=90°，∠X1O1Y1=∠Y1O1Z1=135°，轴向变形系数p=r=1，q=0.5。作图时，一般使O1Z1轴处于垂直位置，则O1X1轴为水平线，O1Y1与水平线成45°，可利用45°三角板方便作出。作形体的斜二测时，只要采用上述的轴间角和轴向变形系数，其作图的步骤和正等测完全一样。图5.12所示即为斜二测的轴间角及轴向变形系数。由此可知斜二测图绘制的最大优点：形体上平行于V面的平面反映实形。

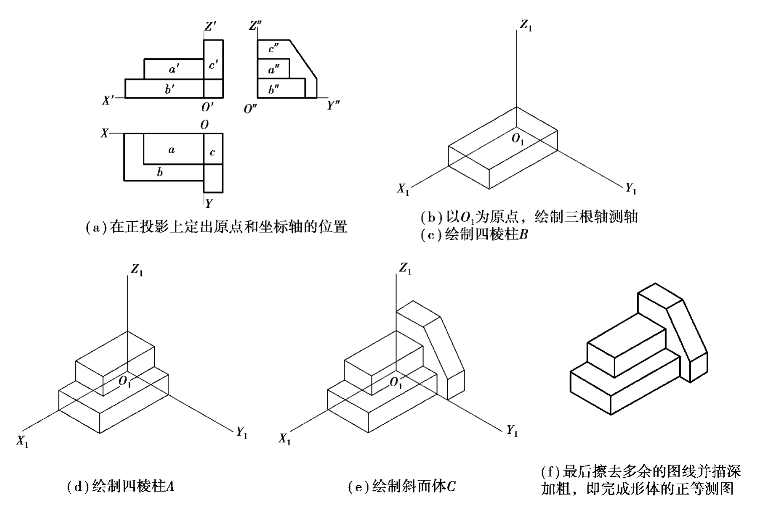
图5.10　叠加法绘制轴测形体的作图步骤

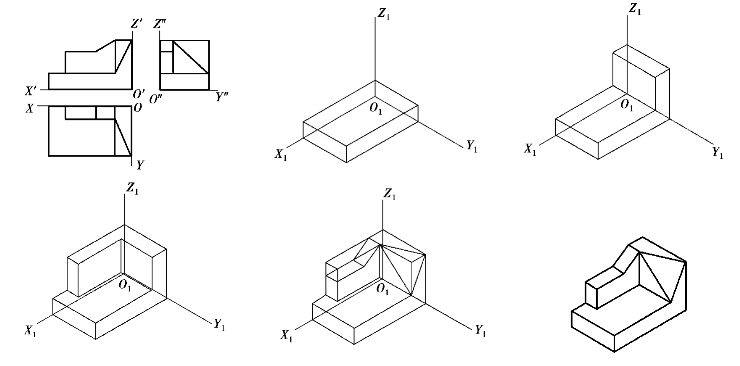
图5.11　综合法绘制形体正等测投影

【例5.8】试画出图示正六棱柱的斜二测图。

【解】作图过程如图5.13所示。

【例5.9】试画出图示六棱锥的斜二测图。

【解】作图过程如图5.14所示。

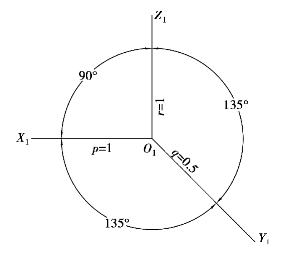
图5.12　斜二测的轴间角及轴向变形系数

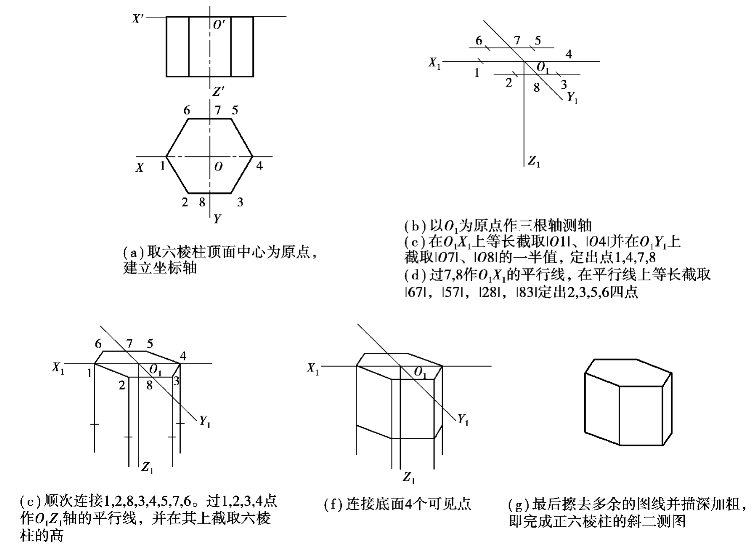
图5.13　正六棱柱的斜二测的作图步骤

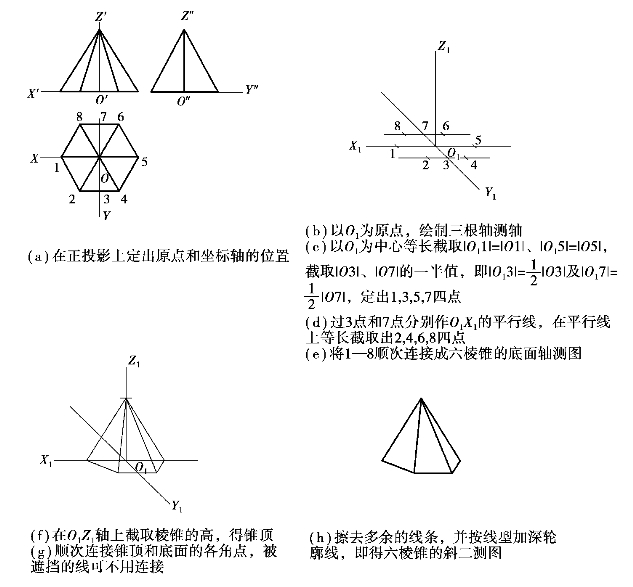
图5.14　六棱锥的斜二测的作图步骤