学建筑识图：棱柱体投影能否写两行左右

由两个互相平行的多边形平面，其余平面均为四边形且每相邻两个四边形平面的交线互相平行的平面围成的基本平面体称为棱柱体。两个互相平行的平面称为底面，其余各面称为棱面，棱面与棱面的交线称为棱线，棱面与底面的交线称为底面边线，两底面间的距离称为棱柱体的高。棱线垂直于底面的棱柱称为直棱柱，如图3.3所示；棱线与底面斜交的棱柱称为斜棱柱，如图3.4所示；底面为正多边形的直棱柱称为正棱柱。依据底面多边形的边数，有三棱柱、四棱柱、五棱柱、六棱柱等。

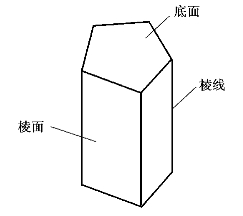
图3.3　直棱柱

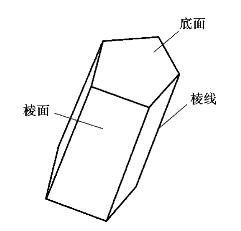
图3.4　斜棱柱

现以直三棱柱为例，来分析棱柱体的投影特性。如图3.5所示，三棱柱由5个平面组成，上、下2个底面（三角形），左、右、后3个棱面（矩形）。为了便于绘制棱柱体的三面正投影图，通常是将棱柱体的底面与投影面平行或垂直放置，由此得出5个平面的空间位置，两个水平面（上、下底面）、一个正平面（后棱面ADFC）、两个铅垂面（左棱面ABDE和右棱面BCEF）。

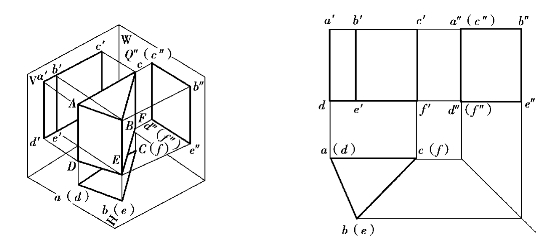
图3.5　三棱柱的投影

由于知道5个面的空间位置，就可得出5个面在3个投影面中的投影，在每个投影图中我们都能找到这5个面的投影。

正面投影是2个矩形，它是两铅垂面（左、右棱面）在V面上的投影（可见，但不反映实形）。两个矩形的外围线框构成的大长方形是正平面（后棱面）的投影（不可见，但反映实形）。大矩形的上、下两条边线是两水平面（上、下底面）的积聚投影。(www.xing528.com)

水平投影是一个三角形，它是上、下两底面的投影（上、下底面重影，上底可见，下底不可见），并反映实形。三角形的3条边是3个棱面的投影（具有积聚性）。

侧面投影是一个矩形，它是左、右两个棱面的投影（左可见右不可见，不反映实形）。矩形上、下两个边分别是上底面和下底面的积聚投影，矩形边线a″d″是后棱面的积聚投影。

为了保证三棱柱的投影对应关系：正面投影和水平投影长对正、正面投影和侧面投影高平齐、水平投影和侧面投影宽相等，这就是三面投影图之间的“三等关系”。

同理，可以画出六棱柱的投影，如图3.6所示。

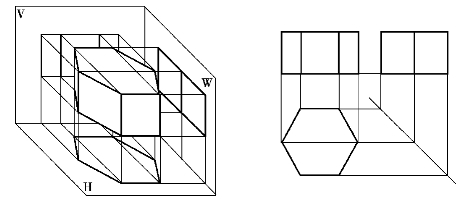
图3.6　六棱柱的投影

综合分析，棱柱体的投影规律如下：

①底面平行的投影面上的投影为多边形，多边形的边数反映棱柱体的棱数。

②另两个投影面上为N个矩形围成的大矩形。