若一点在平面内的一条直线上,则该点必定在这个平面内。
直线在平面内的几何条件如下:
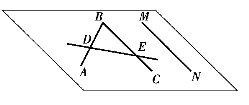
图2.37 直线在平面内的几何条件
①直线通过平面内的两点;如图2.37所示,AB,BC为平面内直线,则DE在平面内。
②直线通过平面内的一点,且平行于该平面上的一条直线。如图2.37所示,BC在平面内,M点在平面内,作MN//BC,则MN在平面内。
只要满足以上两个条件之一的直线,即为该平面内的直线。
【例2.7】已知△ABC及其上一点M的投影m′,求作点M的水平投影m。
【解】方法1:如图2.38所示;方法2:如图2.39所示。

图2.38 补出平面上的点投影(方法1)
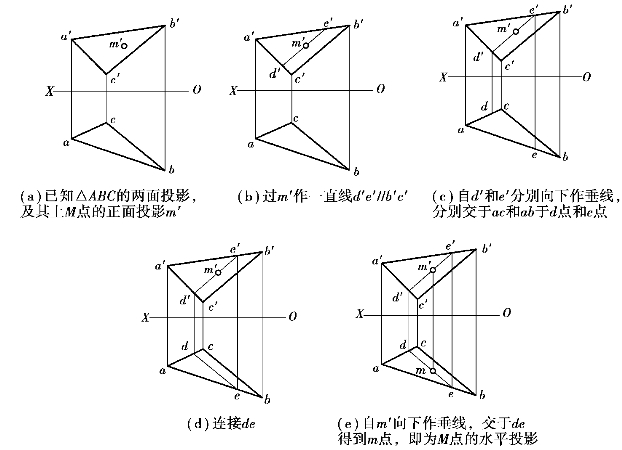
图2.39 补出平面上的点投影(方法2)
【例2.8】完成图示四边形平面的水平投影。
【解】对角线AC和BD的连线交点必在平面ABCD上。解题过程如图2.40所示。
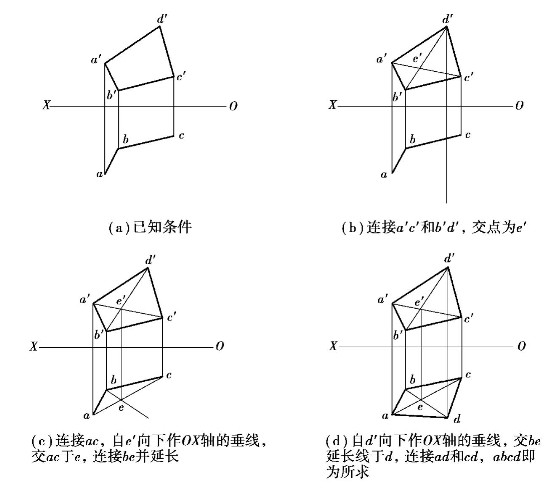
图2.40 求作平面的水平投影(https://www.xing528.com)
本章小结
1.投影的形成有三个要素:投影线(光线)、物体、投影面。投影法分为中心投影法和平行投影法。平行投影分为正投影和斜投影两种。正投影的3大特性有:实形性、积聚性、缩小性。
2.3个互相垂直的投影面H,V,W组成一个三面投影体系。利用正投影原理将物体向这3个投影面投视,即得水平投影、正面投影、侧面投影。3个投影面之间存在的投影关系是:长对正、高平齐、宽相等。
3.任何复杂的形体都可看成是点、直线、平面的组成。点的投影仍是点。当空间两点位于某一投影面的同一直线上时,则此两点的投影重合,这两点称为重影点。直线的投影可能是直线或点。平面的投影可能是平面或直线。根据其对投影面的相对位置不同,投影特性亦不同。
复习思考题
1.点的三面投影规律是什么?
2.点的三个面投影是如何标注的?
3.根据点的两个投影如何求第三个投影,即如何“二补三”?
4.根据点的坐标作出其三面投影图和直观图。
5.什么叫重影点及其可见性的判别?
6.试述直线上点的投影特性。
7.试述平行两直线投影特性。
8.试比较相交两直线和交叉两直线的投影特性。
9.叙述投影面的平行线、投影面的垂直线以及一般位置直线的投影特点。
10.叙述投影面的平行面、投影面的垂直面以及一般位置平面的投影特点。
11.怎样在已知平面上取直线和点?
12.怎样在已知平面上作投影面的平行线?
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




