建筑识图与房屋构造：两直线相对位置

空间两直线的相对位置归纳为三种情况：两直线平行、两直线相交和两直线交叉。其中注意相交和交叉两直线都包含有垂直的特殊情况。

1）两直线平行

（1）投影特性

空间两直线平行，则它们的同面投影必相互平行，且空间两直线的比值等于同面投影的比值，如图2.28所示。

（2）判定

若两直线的各组同面投影相互平行，则两直线在空间中必是平行的。以下分为两种情况来讨论：

①对于一般位置直线，只要任意两组同面投影分别平行，则可判定这两直线在空间是平行的。

②若两直线为某一投影面的平行线，则要用两直线所平行的那个投影面的投影来判断。如图2.29（a）所示，图示两水平线AB和CD的H面和V面投影均平行，即ab//cd，a′b′//c′d′，则可确定两直线平行，即AB//CD。侧平线AB和CD的H面和V面投影是平行的，但是不能确定空间两直线是否平行，所以必须要作出这两条侧平线在W面的投影，才能判定两直线是否空间平行。如图2.29（b）所示，作出W面投影以后，由于a″b″不平行于c″d″，则由此断定直线AB不平行于CD。

图2.28　两直线平行

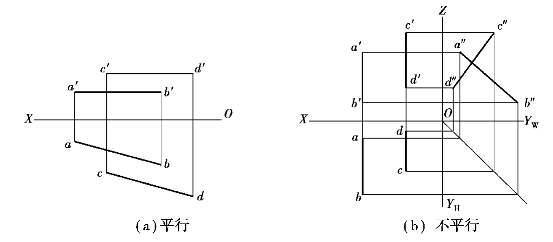
图2.29　判定两直线是否平行

2）两直线相交

（1）投影特性

两直线相交，则它们的同面投影必相交，而且交点是空间同一点的投影，即此交点满足点的三面投影特性，如图2.30所示。

(www.xing528.com)

图2.30　两直线相交

（2）判定

若两直线的各组同面投影分别相交，且满足交点是空间中同一点的三面投影特性，则两直线在空间中必是相交的。

以下分为两种情况来讨论：

①对于两条一般位置直线，只要两组同面投影分别相交，且满足交点是空间同一点的三面投影特性，即可判定两直线在空间中是相交的。

②若两直线中有一条是某一投影面的平行线，则要验证直线在所平行的投影面上的投影是否相交，且满足交点是空间同一点的三面投影特性，如图2.31所示。

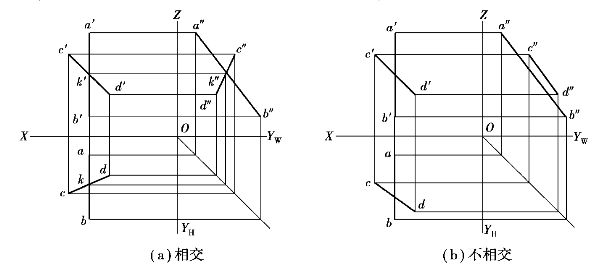
图2.31　判定两直线是否相交

3）两直线交叉

（1）投影特性

空间中两直线既不平行也不相交，则称之为交叉两直线。交叉两直线的各组同面投影可能有平行的，但是不会同时分别平行；同面投影可能有相交，但是交点绝不符合同一点的三面投影特性，因为这三个点投影并不是空间中同一点的三面投影，如图2.32所示。

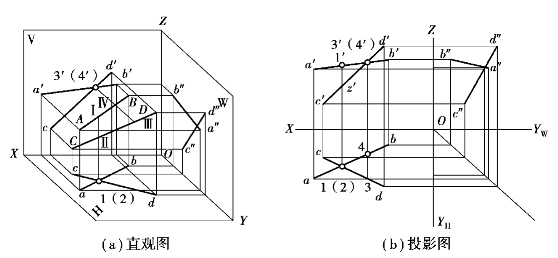
图2.32　两直线交叉

（2）交叉两直线重影点可见性的判别

两条直线交叉，其同面投影的交点为该投影面重影点的投影，可根据其他面上的点判断可见性。如图2.32所示，Ⅰ，Ⅱ点为H面的重影点，通过V面投影来判别，V面投影中，Ⅰ在上，Ⅱ在下，所以从上向下看时，Ⅰ可见，而Ⅱ不可见，H面标注重影点为1（2）；同理，Ⅲ，Ⅳ点为V面的重影点，通过H面投影来判别，H面投影中，Ⅲ在前，而Ⅳ在后，所以从前向后看时，Ⅲ可见，而Ⅳ不可见，V面标注重影点为3′（4′）。