1）从属性
点在线上，则点的各个投影必定在该直线的同面投影上；反之，点的各个投影在直线的同面投影上，则该点一定在空间直线上，这种性质，称为点投影的从属性。
如图2.23所示，点C为直线AB上的一点，则点C的三面投影c，c′，c″必定在直线AB的同面投影ab，a′b′，a″b″上。
2）定比性
直线上点分线段成正比，则分线段的各个同面投影之比等于其线段之比，这种性质称为点投影的定比性。
如图2.23所示，点C为直线AB上的一点，点C将直线段AB分成AC和CB两段。则两直线段AC，CB和其投影之间的关系为：AC∶CB=ac∶cb=a′c′∶c′b′=a″c″∶c″b″。
图2.23 直线上点的投影
【例2.4】已知侧平线AB的两投影ab，a′b′和直线上的点C的正面投影c′，求水平投影c。
本题用两种方法解题，分别为用从属性解题和用定比法解题。
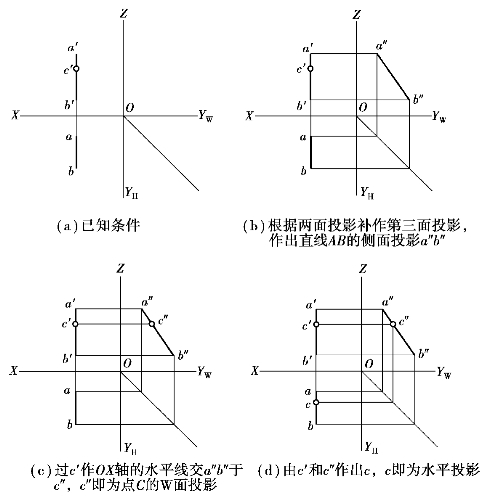
【解】方法1：AB为侧平线，所以不能直接由c′作出c，根据从属性，可知点C在直线上，则点C的各个投影都在直线的同面投影上，即c必在ab，c″必在a″b″上，由此推知作题思路为：先作出直线第三面投影a″b″，利用“高平齐”作出c″，然后根据“二补三”作出c。解题过程如图2.24所示。
(www.xing528.com)
图2.24 求作直线上点（从属性）
方法2：点C在AB上，所以根据定比性质，必定满足a′c′∶c′b′=ac∶cb的比例关系，所以利用定比直接解题，无须求作直线第三面投影。解题过程如图2.25所示。
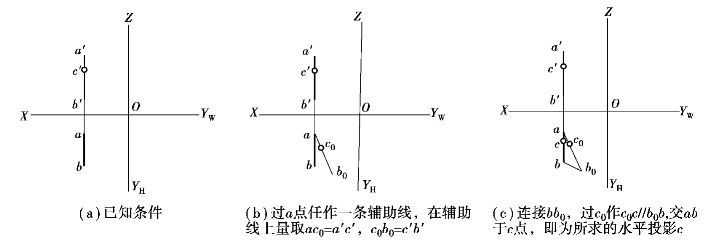
图2.25 求作直线上点（定比性）
【例2.5】判定点C是否在侧平线AB上。
【解】判定即性质的逆过程，要判定点在直线上，有两种方法：
①若点的投影均在直线的同面投影上，则点在直线上；反之，点则不在直线上。解题过程如图2.26所示。
②点分线段成定比，则点在直线上；反之，点则不在直线上。解题过程如图2.27所示。
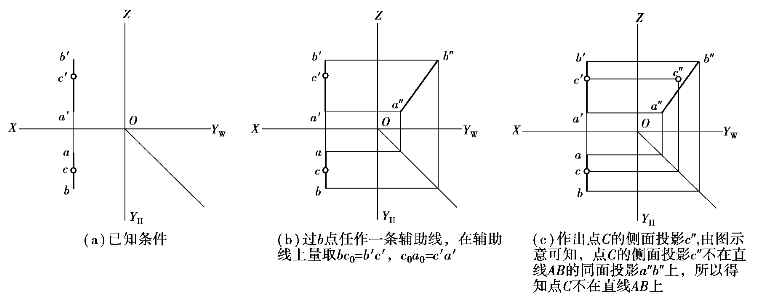
图2.26 判断点是否在直线上（从属性）
图2.27 判断点是否在直线上（定比性）
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
