（一）罕遇地震作用下的弹塑性变形分析
1.“试题”回顾
〖试题4.9.10〗罕遇地震作用下结构变形验算（2000年）
下列关于进行罕遇地震作用下结构变形验算的见解，何项错误？
（A）当遭遇预估的罕遇地震时，结构将产生较大的弹性变形，需予以控制，以免倒塌
（B）为防止结构在罕遇地震中倒塌，体现“大震不倒”的设防目标，必要时应进行第二阶段设计，包括变形验算
（C）应对有特殊要求的建筑和大震中易倒塌结构的易损部位进行塑性变形验算，以实现第三水准的设防要求
（D）对大多数的结构，可只通过强度设计、概念设计和抗震构造措施来满足第三水准的设计要求
2.《规范》规定
《建筑抗震设计规范》规定：
3.6.2 不规则且具有明显薄弱部位可能导致地震时严重破坏的建筑结构，应按本规范有关规定进行罕遇地震作用下的弹塑性变形分析。此时，可根据结构特点采用静力弹塑性分析或弹塑性时程分析方法。
大量震害分析表明，大震作用下一般结构均存在“塑性变形集中”的薄弱层，这种薄弱层仅按承载力计算有时难以发现。这是因为结构构件强度是按小震作用计算的，各截面实际配筋与计算往往不一致，同时各部位在大震下其效应增大的比例也不同，从而使有些层可能率先屈服，形成塑性变形集中。随着地震强度的增加，结构进入弹塑性变形状态，这些塑性变形集中部位的弹塑性变形超过某种限值，形成薄弱部位（薄弱层），就会产生局部倒塌。而局部倒塌往往又会引起整体的坍塌。
图4.9.5 结构弹塑性层间变形分布
结构的时程分析也说明弹塑性层间变形沿高度的分布是不均匀的（图4.9.5）。影响层间变形的主要因素是楼层屈服强度分布，在屈服强度相对较低的薄弱部位，地震作用下将产生很大的塑性层间变形。而其他各层的层间变形相对较小，接近于弹性反应计算结果。因此，在抗震设计中，只要控制了薄弱部位在罕遇地震下的变形，即可控制结构的抗震安全性。
判断薄弱层的部位和验算薄弱层的弹塑性变形是否满足抗震要求，就成了大震不倒验算的主要内容。如果将截面抗震验算和多遇地震下的弹性变形验算合称为第一阶段抗震设计（即解决小震不坏），则罕遇地震下弹塑性变形验算可称为第二阶段抗震设计（解决大震不倒）。
（二）需要进行弹塑性变形验算的范围
1.“试题”回顾
〖试题4.9.11〗薄弱层抗震变形（1999年）
Ⅰ.框架 Ⅱ.框架-剪力墙 Ⅲ.填充墙框架 Ⅳ.剪力墙 V.乙类建筑中的结构
下面哪项列出的结构宜进行罕遇地震作用下的薄弱层抗震变形验算？
（A）Ⅰ、Ⅴ （B）Ⅰ、Ⅱ、Ⅳ （C）Ⅰ、Ⅲ、V （D）Ⅰ、Ⅲ
2.《规范》规定
（1）应进行弹塑性变形验算的结构
《建筑抗震设计规范》规定：
5.5.2 结构在罕遇地震作用下薄弱层的弹塑性变形验算，应符合下列要求：
1 下列结构应进行弹塑性变形验算：
1）8度Ⅲ、Ⅳ类场地和9度时，高大的单层钢筋混凝土柱厂房的横向排架；
2）7～9度时楼层屈服强度系数小于0.5的钢筋混凝土框架结构；
3）高度大于150m的结构；
5）采用隔震和消能减震设计的结构。
《高层建筑混凝土结构技术规程》亦有同样规定：
3.7.4 高层建筑结构在罕遇地震作用下的薄弱层弹塑性变形验算，应符合下列规定：
1 下列结构应进行弹塑性变形验算：
1）7～9度时楼层屈服强度系数小于0.5的框架结构；
2）甲类建筑和9度抗震设防的乙类建筑结构；
3）采用隔震和消能减震设计的建筑结构；
4）房屋高度大于150m的结构。
（2）宜进行弹塑性变形验算的结构
《建筑抗震设计规范》规定：
5.5.2 结构在罕遇地震作用下薄弱层的弹塑性变形验算，应符合下列要求：
2 下列结构宜进行弹塑性变形验算：
1）本规范表5.1.2-1所列高度范围且属于本规范表3.4.2-2所列竖向不规则类型的高层建筑结构；
2）7度Ⅲ、Ⅳ类场地和8度时乙类建筑中的钢筋混凝土结构和钢结构；
3）板柱-抗震墙结构和底部框架砌体房屋；
4）高度不大于150m的其他高层钢结构；
5）不规则的地下建筑结构及地下空间综合体。
《高层建筑混凝土结构技术规程》亦有同样规定：
3.7.4 高层建筑结构在罕遇地震作用下的薄弱层弹塑性变形验算，应符合下列规定：
2 下列结构宜进行弹塑性变形验算：
1）本规程表4.3.4所列高度范围且不满足本规程第3.5.2～3.5.6条规定的竖向不规则高层建筑结构；
2）7度Ⅲ、IV类场地和8度抗震设防的乙类建筑结构；
3）板柱-剪力墙结构。
以上规定是为了在满足抗震设计基本要求的前提下，尽量减少设计计算工作量。所以，根据震害调查及科学研究结果，只要求对上述在大地震中较易倒塌的延性结构和特殊要求的钢筋混凝土建筑进行薄弱层或薄弱部位的变形验算。
（三）结构薄弱层（部位）位置判断
研究表明，结构弹塑性层间变形与多种因素有关，但主要取决于楼层屈服强度系数的大小及楼层屈服强度系数沿房屋高度的分布情况。对混凝土结构，薄弱层的确定主要用楼层屈服强度系数来判别。当此系数大于0.5时，这种楼层可不必再验算弹塑性变形。当此系数等于或小于0.5时，则必须进一步验算该层的弹塑性变形是否满足《建筑抗震设计规范》要求。
1.“试题”回顾
〖试题4.9.12〗结构薄弱层（2002年）
试问，对于下列关于建筑结构薄弱层特征及有关规定的论述，其中何项是错误的？
（A）在地震作用下，建筑结构出现塑性变形集中的楼层，称为薄弱层
（B）在地震作用下，在薄弱层处必定首先屈服，而结构的倒塌极大可能就是在这个区域开始
（C）为了防止结构倒塌，应按规定设防烈度对高层建筑结构进行抗震变形验算
（D）框架结构薄弱层层间弹塑性位移Δup，应符合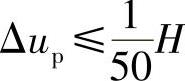
的要求，式中H为薄弱层部位的层高
2.《规范》规定
（1）“楼层屈服强度系数”的计算方法
《建筑抗震设计规范》5.5.2条讲述了“楼层屈服强度系数”的计算方法：
5.5.2
注：楼层屈服强度系数为按钢筋混凝土构件实际配筋和材料强度标准值计算的楼层受剪承载力和按罕遇地震作用标准值计算的楼层弹性地震剪力的比值；对排架柱，指按实际配筋面积、材料强度标准值和轴向力计算的正截面受弯承载力与按罕遇地震作用标准值计算的弹性地震弯矩的比值。
《高层建筑混凝土结构技术规程》亦有同样规定：
3.7.4
注：楼层屈服强度系数为按构件实际配筋和材料强度标准值计算的楼层受剪承载力与按罕遇地震作用计算的楼层弹性地震剪力的比值。
结构第i层楼层屈服强度系数ξy（i）可表示为
ξy（i）=Vy（i）/Vu（i） （4.9.1）
式中 ξy（i）——楼层屈服强度系数，按构件实际配筋和材料强度标准值计算的楼层受剪承载力和楼层弹性地震剪力的比值；
Vy（i）——第i层受剪实际承载力，根据第一阶段设计所得到的截面实际配筋和材料强度标准值计算；
Vu（i）——第i层弹性地震剪力，计算时水平地震影响系数最大值αmax应采用罕遇地震时的数值。
（2）结构薄弱层（部位）的确定
楼层屈服强度系数ξy反映了结构中楼层所具有的实际强度与该楼层所受罕遇地震下弹性地震剪力的相对关系。两者差值越大则ξy越小，说明该楼层最弱，有可能率先屈服，出现较大弹塑性层间变形。根据数千个1～15层剪切型结构弹塑性时程分析的结果可知另一个规律是：多层结构存在“塑性变形集中”的薄弱层是一种普遍现象。薄弱层的位置对于屈服强度系数沿高度分布均匀的结构多在底层，分布不均匀的结构则在ξy最小处或相对较小处；单层厂房往往在上柱。《建筑抗震设计规范》5.5.4条第1款讲述了这一规律。
5.5.4 结构薄弱层（部位）弹塑性层间位移的简化计算，宜符合下列要求：
1 结构薄弱层（部位）的位置可按下列情况确定：
1）楼层屈服强度系数沿高度分布均匀的结构，可取底层；
2）楼层屈服强度系数沿高度分布不均匀的结构，可取该系数最小的楼层（部位）和相对较小的楼层，一般不超过2～3处；
3）单层厂房，可取上柱。
《高层建筑混凝土结构技术规程》亦有同样规定：
5.5.3 结构薄弱层（部位）的弹塑性层间位移的简化计算，宜符合下列规定：
1 结构薄弱层（部位）的位置可按下列情况确定：
1）楼层屈服强度系数沿高度分布均匀的结构，可取底层；
2）楼层屈服强度系数沿高度分布不均匀的结构，可取该系数最小的楼层（部位）和相对较小的楼层，一般不超过2～3处。
（四）结构薄弱层（部位）弹塑性层间位移简化计算法的适用范围
除了时程分析法直接计算弹塑性变形外，根据对数千个1层～15层剪切型结构弹塑性时程分析结果得到以下统计规律：多层剪切型结构薄弱层的弹塑性变形与弹性变形之间有相对稳定的关系。根据此规律给出了近似简化计算变形方法，即《建筑抗震设计规范》中给出的将弹性层间变形乘以放大系数来求弹塑性层间变形，称为弹塑性变形简化计算法。
1.“试题”回顾
〖试题4.9.13〗弹塑性变形简化计算法（2010年）
下列关于高层建筑混凝土结构在罕遇地震作用下薄弱层弹塑性变形验算的相关论述，其中何项不正确？
（A）采用隔震和消能减震技术的建筑结构，应进行薄弱层弹塑性变形验算
（B）采用弹塑性动力时程分析方法进行薄弱层验算时，应按建筑场地类别和所处地震动参数区划的特征周期选用不少于两组实际地震波和一组人工模拟的地震波的加速度时程曲线
（C）进行高层建筑结构薄弱层弹塑性变形验算时，不需考虑重力二阶效应的不利影响
（D）不超过12层且层刚度无突变的钢筋混凝土框架结构的薄弱层弹塑性变形计算，可采用规范规定的简化计算方法
2.《规范》规定
《建筑抗震设计规范》5.5.3条：
5.5.3 结构在罕遇地震作用下薄弱层（部位）弹塑性变形计算，可采用下列方法：
1 不超过12层且层刚度无突变的钢筋混凝土框架结构、单层钢筋混凝土柱厂房可采用本规范第5.5.4条的简化计算法。
2 除1款以外的建筑结构，可采用静力弹塑性分析方法或弹塑性时程分析法等。
3 规则结构可采用弯剪层模型或平面杆系模型，属于本规范第3.4节规定的不规则结构应采用空间结构模型。
《高层建筑混凝土结构技术规程》亦有同样规定：
5.5.2 在预估的罕遇地震作用下，高层建筑结构薄弱层（部位）弹塑性变形计算可采用下列方法：
1 不超过12层且层侧向刚度无突变的框架结构可采用本规程第5.5.3条规定的简化计算法。
2 除第1款以外的建筑结构可采用弹塑性静力或动力分析方法。
（五）结构薄弱层（部位）弹塑性层间位移的简化计算
对于刚度及屈服强度系数ξy沿高度分布均匀的框架，大量计算结果的统计分析表明，弹塑性层间位移值可近似用同样罕遇地震作用下弹性层间位移值乘增大系数ηp求得。
1.“试题”回顾
〖试题4.9.14〗～〖试题4.9.15〗（2004年）
某一建于7度地震区的10层钢筋混凝土框架结构，抗震设防类别为丙类，设计地震分组为第一组，设计基本地震加速度为0.15g，场地类别为Ⅱ类。非承重填充墙采用砖墙，墙体较少，周期折减系数为0.7，底层层高6m，楼层屈服强度系数ξy为0.45，结构自振周期T=1.0s，阻尼比取0.05。
〖试题4.9.14〗薄弱层的位移（2004年）
假定该框架底层屈服强度系数是相邻上层该系数的0.55倍，底层各柱轴压比均大于0.5，且不考虑重力二阶效应及结构稳定方面的影响，试问，在罕遇地震作用下按弹性分析的层间位移Δue的最大值（mm），接近下列何值时才能满足《高层建筑混凝土结构技术规程》中规定的对结构薄弱层（部位）层间弹性位移的要求？
提示：底层在罕遇地震作用下的弹塑性变形，可按《高层建筑混凝土结构技术规程》中的简化计算法计算。
（A）44.6 （B）63.2 （C）98.6 （D）120
〖试题4.9.15〗弹塑性变形（2004）
假定由计算分析得知，该框架结构弹性等效侧向刚度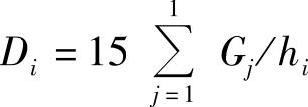
。试问，在罕遇地震作用下，底层考虑重力二阶效应的层间弹塑性位移Δup′，与未考虑重力二阶效应的层间弹塑性位移Δup之比，最接近下列何项数值？
（A）0.5 （B）0.833 （C）1.0 （D）1.2
〖试题4.9.16〗～〖试题4.9.17〗（2009年）
某12层现浇钢筋混凝土框架结构，质量及侧向刚度沿竖向比较均匀，其地震设防烈度为8度，丙类建筑，Ⅱ类建筑场地。底层屈服强度系数ξy为0.4，且不小于上层该系数平均值的0.8倍；柱轴压比大于0.4。
〖试题4.9.16〗层间弹塑性变形（2009年）
已知框架底层总抗侧刚度为8×105kN/m。为满足结构层间弹塑性位移限值。试问，在多遇地震作用下，按弹性分析的底层水平剪力最大标准值与下列何项数值最为接近？
提示：①不考虑重力二阶效应。②从底层层间弹塑性位移限值入手。
（A）5000kN （B）6000kN （C）7000kN （D）8000kN
〖试题4.9.17〗层间弹塑性变形（2009年）
条件同〖试题4.9.16〗。在多遇地震作用下，未考虑重力二阶效应的影响，达到结构层间弹塑性位移限值时，按弹性分析的底层水平剪力标准值为V0。试问，如考虑重力二阶效应的影响，其底层多遇地震弹性水平剪力标准值不超过下列何项数值时，才能满足层间弹塑性位移限值的要求？
（A）0.8V0 （B）0.83V0 （C）1.0V0 （D）1.2V0
〖试题4.9.18〗弹塑性变形（2009年）
某10层现浇钢筋混凝土框架结构，地下一层箱形基础顶为嵌固端，房屋高度为36.4m。首层层高为4.0m，2～10层层高均为3.6m。该房屋为丙类建筑，抗震设防烈度为8度，设计基本地震加速度为0.20g，框架抗震等级为一级。
沿该建筑物竖向框架结构的层刚度无突变，楼层屈服强度系数ξy分布均匀。已求得首层的楼层屈服强度系数ξy=0.45。1～3层柱截面及其混凝土强度等级、配筋均相同。按实配钢筋和材料强度标准值计算的边柱、中柱的受剪承载力分别为：边柱Vcua1=678kN，中柱Vcua2=960kN。罕遇地震作用下首层弹性地震剪力标准值为36000kN。试问，下列何项主张符合相关规范的规定？
提示：按《建筑抗震设计规范》GB 50011—2001（2008年版）作答。
（A）不必进行弹塑性变形验算
（B）需进行弹塑性变形验算，且必须采用静力弹塑性分析方法或弹塑性时程分析法
（C）通过调整柱实配钢筋使Vcua1和Vcua2增加5%后，可不进行弹塑性变形验算
（D）可采用弹塑性变形的简化计算方法，将罕遇地震作用下按弹性分析的层间位移乘以增大系数1.90
〖试题4.9.19〗（2011年）
某12层现浇框架结构，其中一榀中部框架的剖面如图4.9.6所示，现浇混凝土楼板，梁两侧无洞。底层各柱截面相同，2～12层各柱截面相同，各层梁截面均相同。梁、柱矩形截面线刚度ib0、ic0（单位：1010N·mm）标注于构件旁侧。假定，梁考虑两侧楼板影响的刚度增大系数取《高层建筑混凝土结构技术规程》JGJ 3—2002中相应条文中的最大值。假定，该建筑物位于7度抗震设防区，调整构件截面后，经抗震计算，底层框架总侧移刚度ΣD=5.2×105N/mm，柱轴压比大于0.4，楼层屈服强度系数为0.4，不小于相邻层该系数平均值的0.8。试问，在罕遇水平地震作用下，按弹性分析时作用于底层框架的总水平组合剪力标准值VEK（kN），最大不能超过下列何值才能满足规范对位移的限值要求？
提示：1.按《建筑抗震设计规范》GB 50011—2010作答。
2.结构在罕遇地震作用下薄弱层弹塑性变形计算可采用简化计算法；不考虑重力二阶效应。
图 4.9.6
3.不考虑柱配箍影响。
（A）5.6×103 （B）1.1×104
（C）3.1×104 （D）6.2×104
〖试题4.9.20〗弹塑性层间位移角计算（2013年一级）
某70层办公楼，平、立面如图4.9.7所示，采用钢筋混凝土筒中筒结构，抗震设防烈度为7度，丙类建筑，Ⅱ类建筑场地。房屋高度地面以上为250m，质量和刚度沿竖向分布均匀。已知小震弹性计算时，振型分解反应谱法求得的底部地震剪力为16000kN，最大层间位移角出现在k层，θk=1/600。
假定，正确选用的7条时程曲线分别为：AP1～AP7，同一软件计算所得的第k层结构的层间位移角（同一层）见表4.9.1。试问，估算的大震下该层的弹塑性层间位移角参考值最接近下列何项数值？(www.xing528.com)
提示：按《建筑抗震设计规范》GB 50011—2010作答。
图 4.9.7
a）平面图 b）立面图
表 4.9.1
（续）
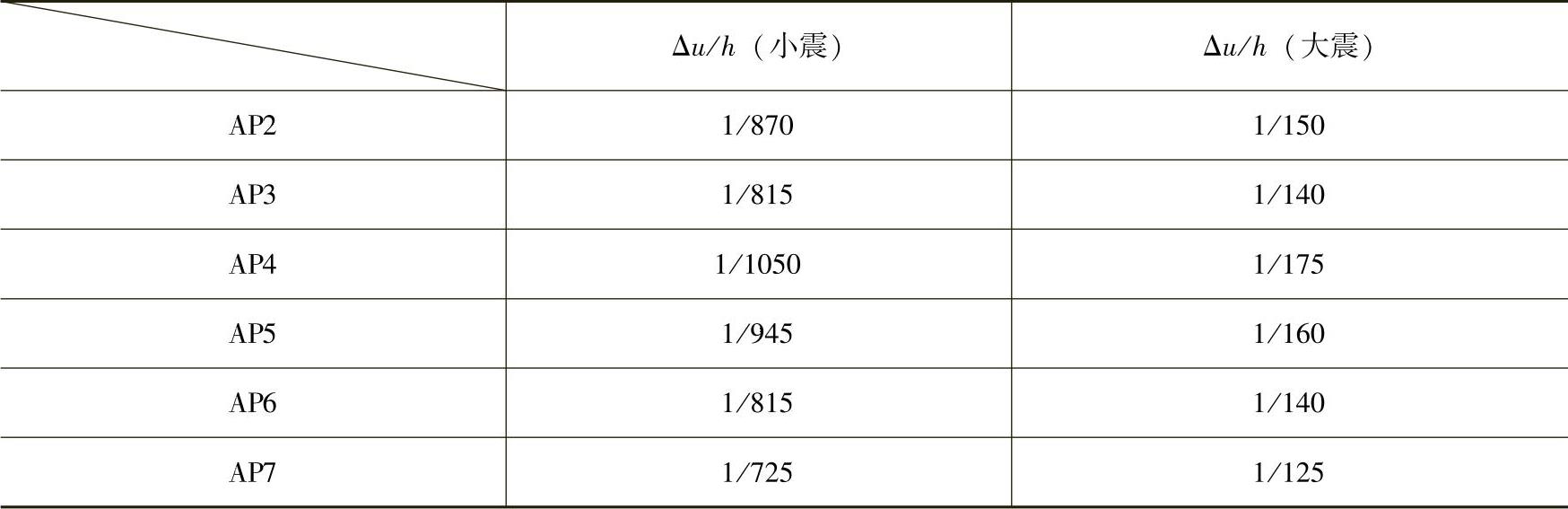
（A）1/90 （B）1/100
（C）1/125 （D）1/145
2.《规范》规定
《建筑抗震设计规范》5.5.4条第2款：
5.5.4 结构薄弱层（部位）弹塑性层间位移的简化计算，宜符合下列要求：
2 弹塑性层间位移可按下列公式计算：
Δup=ηpΔue（5.5.4-1）
或
式中 Δup——弹塑性层间位移；
Δuy——层间屈服位移；
μ——楼层延性系数；
Δue——罕遇地震作用下按弹性分析的层间位移；
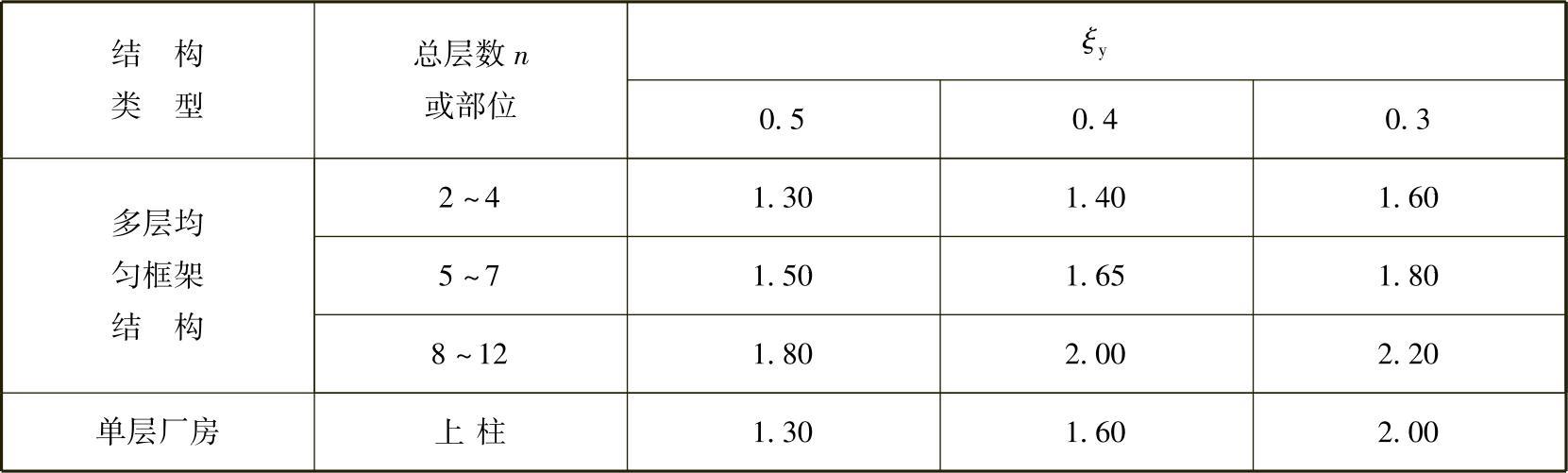
ηp——弹塑性层间位移增大系数，当薄弱层（部位）的屈服强度系数不小于相邻层（部位）该系数平均值的0.8时，可按表5.5.4采用。当不大于该平均值的0.5时，可按表内相应数值的1.5倍采用；其他情况可采用内插法取值；
ξy——楼层屈服强度系数。
表5.5.4 弹塑性层间位移增大系数
《高层建筑混凝土结构技术规程》亦有同样规定：
5.5.3 结构薄弱层（部位）的弹塑性层间位移的简化计算，宜符合下列规定：
2 弹塑性层间位移可按下列公式计算：
Δup=ηpΔue（5.5.3-1）
或
式中 Δup——弹塑性层间位移（mm）；
Δuy——层间屈服位移（mm）；
μ——楼层延性系数；
Δue——罕遇地震作用下按弹性分析的层间位移（mm）。计算时，水平地震影响系数最大值应按本规程表4.3.7-1采用；
ηp——弹塑性位移增大系数，当薄弱层（部位）的屈服强度系数不小于相邻层（部位）该系数平均值的0.8时，可按表5.5.3采用；当不大于该平均值的0.5时，可按表内相应数值的1.5倍采用；其他情况可采用内插法取值；
ξy——楼层屈服强度系数。
表5.5.3 结构的弹塑性位移增大系数ηp
（六）弹塑性层间位移角限值
1.“试题”回顾
〖试题4.9.21〗弹塑性位移角限值（2008年）
对于下列的一些论点，根据《高层建筑混凝土结构技术规程》JGJ3—2002判断，其中何项是不正确的？
（A）在正常使用条件下，限制高层建筑结构层间位移的主要目的之一是保证主结构基本处于弹性受力状态
（B）验算按弹性方法计算的层间位移角Δu/h是否满足规程限值要求时，其楼层位移计算不考虑偶然偏心影响
（C）对于框架结构，框架柱的轴压比大小，是影响结构薄弱层层间弹塑性位移角[θp]限值取值的因素之一
（D）验算弹性层间位移角Δu/h限值时，第i层层间最大位移差Δui是指第i层与第i-
1层在楼层平面各处位移的最大值之差，即Δui=ui，max-ui-1，max
2.《规范》规定
《建筑抗震设计规范》5.5.5条给出了结构薄弱层（部位）弹塑性层间位移角限值：
5.5.5 结构薄弱层（部位）弹塑性层间位移应符合下式要求：
Δup≤[θp]h （5.5.5）
式中 [θp]——弹塑性层间位移角限值，可按表5.5.5采用；对钢筋混凝土框架结构，当轴压比小于0.40时，可提高10%；当柱子全高的箍筋构造比本规范第6.3.9条规定的体积配箍率大30%时，可提高20%，但累计不超过25%。
h——薄弱层楼层高度或单层厂房上柱高度。
表5.5.5 弹塑性层间位移角限值
《高层建筑混凝土结构技术规程》亦有同样规定：
3.7.5 结构薄弱层（部位）层间弹塑性位移应符合下式规定：
Δup≤[θp]h （3.7.5）
式中 Δup——层间弹塑性位移；
[θp]——层间弹塑性位移角限值，可按表3.7.5采用；对框架结构，当轴压比小于0.40时，可提高10%；当柱子全高的验筋构造采用比本规程中框架柱箍筋最小配箍特征值大30%时，可提高20%，但累计提高不宜超过25%；
h——层高。
表3.7.5 层间弹塑性位移角限值
（七）算例
【例4.9.2】 在罕遇地震作用下按弹性分析的层间位移Δue的最大值
条件：某一建于7度地震区的10层钢筋混凝土框架结构，底层层高6m，楼层屈服强度系数ξy为0.45。底层屈服强度系数是相邻上层该系数的0.55倍，且不考虑重力二阶效应及结构稳定方面的影响。
要求：求在罕遇地震作用下按弹性分析的层间位移Δue的最大值。
提示：底层在罕遇地震作用下的弹塑性变形，可按《建筑抗震设计规范》中的简化计算法计算。
解答：根据《建筑抗震设计规范》第5.5.5条，
根据《建筑抗震设计规范》第5.5.4条，Δup=ηpΔue，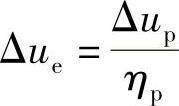
当ξy1＜0.5ξy2，
当0.50ξy1＞0.45ξy2，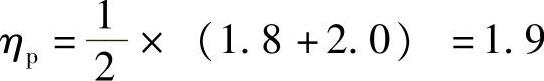
因为ξy1=0.55ξy2，线性内插，取ηp=2.69
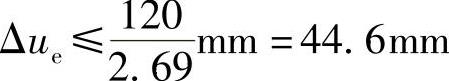
【例4.9.3】 罕遇地震作用下薄弱层的抗震变形验算
条件：某一层高为4.0m的10层钢筋混凝土框架结构，如图4.9.8所示。位于8度（0.20g）抗震设防区。底层、2层及3层的柱截面、配筋相同，且均为C40混凝土。边柱截面尺寸为400mm×400mm，中柱截面尺寸为500mm×500mm，每榀横向框架的侧向刚度为89477kN/m。经抗震计算，已知：
（1）在罕遇地震作用下，该楼共承受总水平地震作用标准值FEK为61875kN。
（2）底层边柱、底层中柱的轴压比均大于0.40。
（3）按柱的实际配筋和混凝土的强度标准值所算得的每根底层边柱、每根底层中柱的抗剪承载力分别为550kN和800kN。
（4）柱子全高的箍筋大于最小含箍特征值30%。
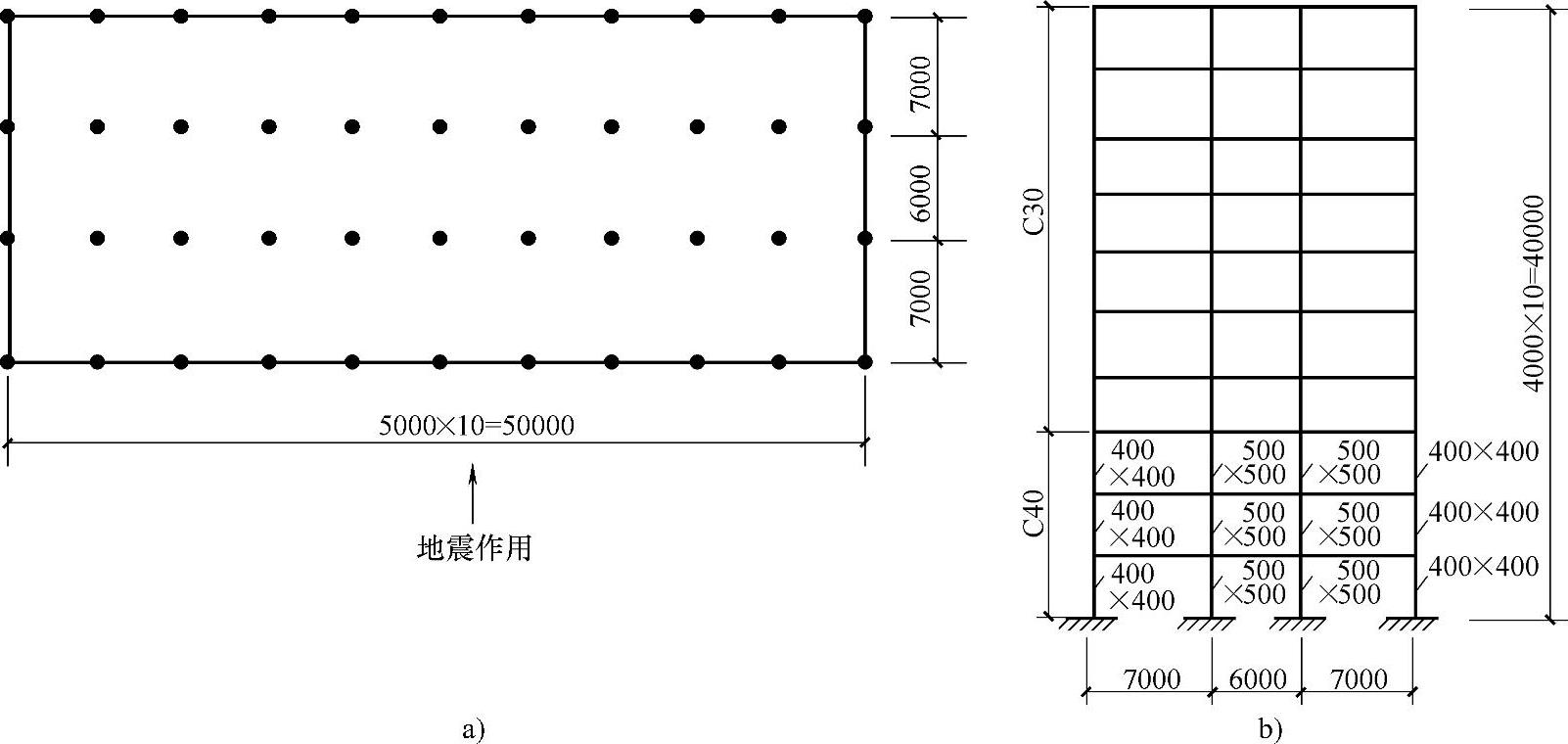
图 4.9.8
a）平面图 b）剖面图
要求：求罕遇地震作用下的薄弱层抗震变形验算。
解答：（1）判断是否需要进行罕遇地震作用下薄弱层的抗震变形验算
已知8度罕遇地震作用下结构基底弹性地震剪力V0=61875kN。
该楼底层共有22根边柱和22根中柱用以抗剪，因此该楼底层的楼层屈服强度系数ξy：
根据《建筑抗震设计规范》第5.5.2条，该框架需要进行罕遇地震作用下薄弱层的抗震变形验算。
（2）对薄弱层作抗震变形验算
根据《建筑抗震设计规范》第5.5.3、第5.5.4条，框架层数小于12层，且其侧向刚度无突变，可按规范简化方法计算Δup。薄弱层就在此ξy沿竖向均匀分布的结构的底层。
1）求罕遇地震作用下，按弹性分析时的层间弹性侧移Δue。
每榀横向框架的侧向刚度为89477kN/m，在罕遇地震作用下，按弹性分析得薄弱层（即底层结构）的弹性层间侧移：
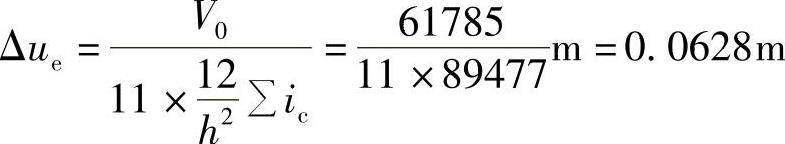
2）求结构薄弱层的层间弹塑性侧移Δup
已算得ξy=0.48，第2、3层的配筋柱的截面尺寸、混凝土强度等级又均与底层柱相同，因而底层、2层及3层的楼层屈服强度系数基本相同，满足薄弱层（底层）的屈服强度系数不小于相邻层该系数平均值的0.8的要求。根据《建筑抗震设计规范》，查得弹塑性位移增大系数为ηp=1.84。因此，Δup=1.84×0.0628m=0.1156m。
3）弹塑性抗震变形验算。根据《建筑抗震设计规范》第5.5.5条，框架结构的弹塑性层间位移角限值[θp]为1/50，当轴压比小于0.4时可提高10%；当柱子全高的箍筋大于最小配箍特征值30%时，又可提高20%，但累计不超过25%。因此，该结构的[θp]取为1.2×1/50=0.024。Δup=0.1156m＞[θp]h=0.024×4m=0.096m，不符合要求。
【例4.9.4】 某12层现浇框架结构，其中一榀中部框架的剖面如图4.9.9所示，现浇混凝土楼板。底层各柱截面相同，2～12层各柱截面相同，各层梁截面均相同。假定，该建筑物位于7度抗震设防区，经计算，底层框架总侧移刚度ΣD=5.2×105N/mm，柱轴压比大于0.4，楼层屈服强度系数为0.4，不小于相邻层该系数平均值的0.8。
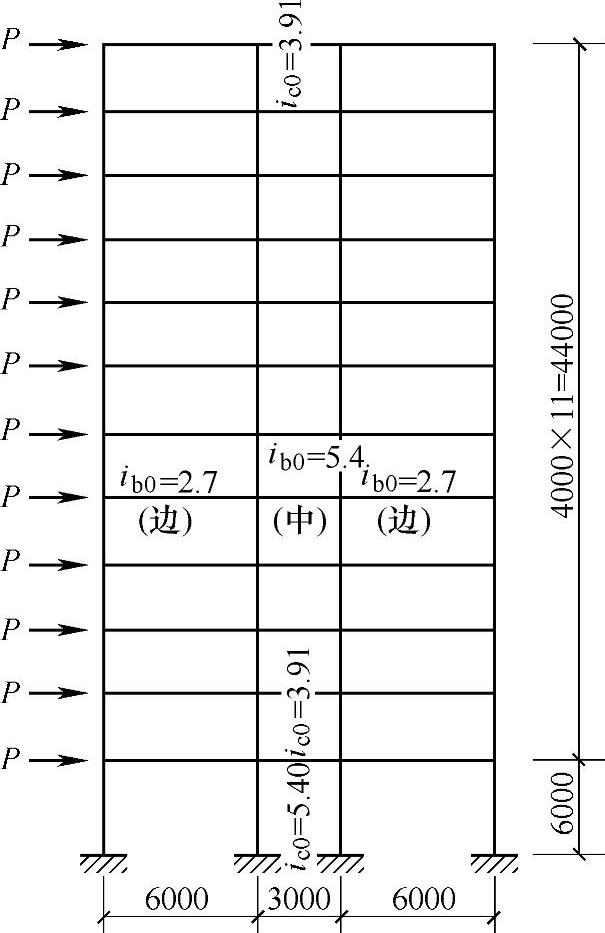
图 4.9.9
试问，在罕遇水平地震作用下，按弹性分析时作用于底层框架的总水平组合剪力标准值VEK（kN），最大不能超过下列何值才能满足规范对位移的限值要求？
提示：1.结构在罕遇地震作用下薄弱层弹塑性变形计算可采用简化计算法；不考虑重力二阶效应。
2.不考虑柱配箍影响。
3.计算内力和位移时，采用D值法。
（A）5.6×103 （B）1.1×104 （C）3.1×104 （D）6.2×104
答案：（C）
根据《建筑抗震设计规范》5.5.2-2条，该结构应进行弹塑性变形验算
根据《建筑抗震设计规范》5.5.5条，最大弹塑性层间位移：Δup≤[θp]h
根据《建筑抗震设计规范》表5.5.5，
根据《建筑抗震设计规范》式（5.5.4-1），
查《建筑抗震设计规范》表5.5.4，ηp=2，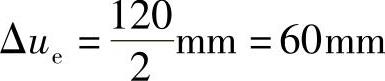
VEK=ΣDi·Δue=5.2×105×60N=3.12×107N=3.12×104kN
（八）模拟考题
[4.9.1] 某幢7层钢筋混凝土框架结构房屋，底层层高为4.5m，其余层层高均为4m。假定底层的楼层屈服强度系数ξy=0.35，并且不大于相邻层楼层屈服强度系数平均值的0.5，满足规范要求在罕遇地震作用下，其底层的最大弹性层间位移Δue（mm），与下列何项数值最接近？
（A）56 （B）62 （C）40 （D）35
答案：（D）
ηp=（1.65+1.80）/2=1.725，应乘以1.5，ηp=1.5×1.725=2.5875
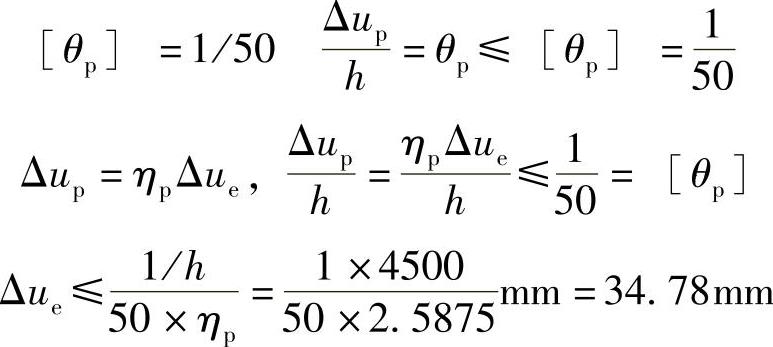
[4.9.2] 一幢8层的钢筋混凝土框架结构（图4.9.10），8度（0.2g），已知罕遇地震作用下的底层弹性层间位移Δue=8mm和底层的楼层屈服强度系数ξy=0.4，不小于相邻层该系数平均值的0.8。在罕遇地震作用下底层的弹塑性层间位移角θp最接近下列何项数值？
（A）1/150 （B）1/250 （C）1/200 （D）1/220
答案：（B）
ξy=0.4的8层框架ηp=2.0，
Δup=ηpΔue=2.0×8mm=16mm
图 4.9.10
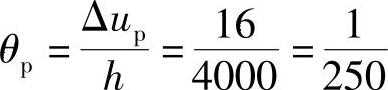，故选（B）。
[4.9.3] 某幢7层钢筋混凝土框架结构房屋，底层层高为4.5m，若底层在多遇地震作用下的弹性层间位移为5mm，在罕遇地震作用下的弹性层间位移为8mm；底层的楼层屈服强度系数ξy=0.4，并且不大于相邻层楼层屈服强度系数平均值的0.5，则在罕遇地震作用下该结构底层的弹塑性层间位移角θp，1与下列何项数值最接近？
（A）1/235 （B）1/227 （C）1/327 （D）1/310
答案：（B）
Δue=8mm，ηp=1.65×1.5=2.475
Δup=ηpΔue=2.475×8mm=19.8mm
θp=Δup/h=19.8/4500=1/227＜[θp]=1/50，满足要求。
[4.9.4] 题干见〖试题4.9.20〗（2013年一级）
答案：（B）
同一楼层弹塑性层间位移与小震弹性层间位移之比分别为：
5.8，5.8，5.82，6.0，5.91，5.82，5.8
根据《抗规》第3.10.4条条文说明：
取平均值时：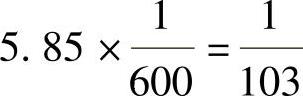
；取最大值时：
故选（B）。
[4.9.5] 舒适度（2014年一级）
某高层建筑裙楼商场内人行天桥，采用钢-混凝土组合结构，如图4.9.11所示，天桥跨度28m，假定，天桥竖向自振频率为fn=3.5Hz，结构阻尼比β=0.02，单位面积有效重量W=5kN/m2。试问，满足楼盖舒适度要求的最小天桥宽度B（m），与下列何项数值最为接近？
图 4.9.11
提示：①按《高层建筑混凝土结构技术规程》JGJ3—2010作答。②接近楼盖自振频率时，人行走产生的作用力Fp=0.12kN。
（A）1.80 （B）2.60 （C）3.30 （D）5.00
答案：（B）
根据《高规》3.7.7条，由《高规》表3.7.7插值，得最大加速度为：
αp=0.22+（3.5-2）×（0.15-0.22）/（4-2）=0.22-0.0525=0.1675
根据《高规》A.0.2，
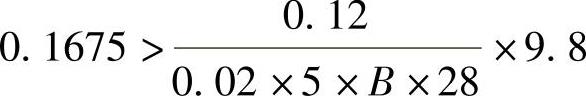，解得B＞2.5m。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
