振型分解法实例：结构工程师专考中的建筑抗震设计技巧

（一）多质点弹性体系自由振动的主振型

振型，即质点体系的振动形式（或形状）。图4.2.6表示在一般初始条件下，两质点体系的质点在振动过程中某瞬间的振型。它是由两个主振型（第一振型、第二振型）的简谐振动叠加而成的复合振动。

主振型是一个特殊的振动形式（或形状），即这质点体系在自由振动过程中对应于各自的自振频率ω_i作简谐振动。在振动过程中的任意时刻，两质点的位移比值（或振动曲线形状）始终保持不变，只改变大小和方向，故与时间无关。相应于ω₁的振动形式称为第一主振型（简称第一振型或基本振型）：相应于ω2的振动形式称为第二主振型（简称第二振型）。因为主振型只取决于质点位移之间的相对值，在实际工程计算绘制振型曲线时，常将其中某一个质点的位移值定为1，其他质点的位移可根据相应比值确定。

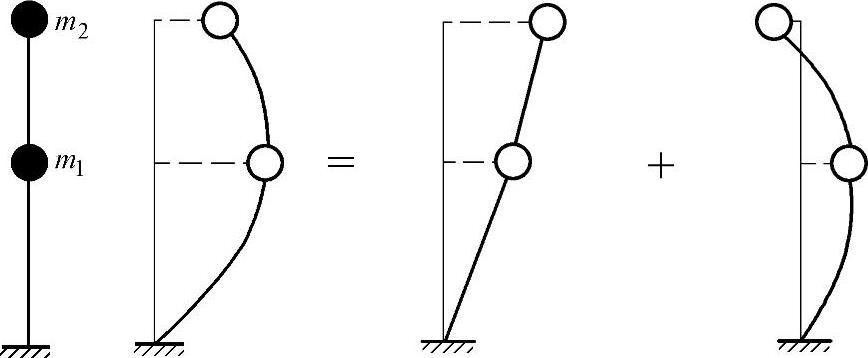
图4.2.6 两质点体系的振型

由于某一主振型在振动过程中不仅各质点间的位移始终保持一定的比值并同时达到各自最大的幅值，显然各质点的速度也保持这一比值。所以只有各质点初位移的比值和初速度的比值均与该主振型的各质点间位移振幅比值相同时，在这样特定的初始条件下，才会出现这种振型的振动形式。

主振型是弹性体系的重要固有特征，它们完全取决于体系的质量和刚度的分布，体系有多少个自由度就有多少个频率，相应地就有多少个主振型。图4.2.7列出的三个质点体系，它有三个主振型，其中质点1的位移值定为1.000，其他质点的位移按相应比值表示。

一般初始条件下，体系的振动曲线将包含全部振型。任一质点的振动都是由各主振型的简谐振动叠加而成的复合振动，它不再是简谐振动，而且质点之间位移的比值也不再是常数，而是随时间发生变化的。

对于n个自由度的弹性体系，相应的有n个自振频率和n个主振型，除第一主振型外的其他振型统称为高阶振型。n自由度弹性体系自由振动时，任一质点的振动都是由n个主振型的简谐振动叠加而成。试验结果表明，振型越高，阻尼作用造成的衰减越快，所以通常高振型只在振动初始才比较明显，以后逐渐衰减，在建筑抗震设计时通常只考虑较低的几个振型的影响。

（二）多质点弹性体系自由振动主振型的正交性

现以两个自由度弹性体系为例来进行讲述，如图4.2.8所示两自由度弹性体系分别按频率ω₁和ω₂作简谐振动时，两个振型的变形曲线及两质点上相应的惯性力如图所示，惯性力表示为m_iω²_ix_ji，其中i为质点编号，j为振型序号。因为结构在任一瞬时的位移等于这一瞬时的惯性力所产生的静力位移，故主振型的变形曲线可视为体系按某一频率振动时，其上相应的惯性力所引起的静力变形曲线。

根据功的互等定理，第一主振型上的惯性力在第二主振型的位移上所做的功等于第二主振型上的惯性力在第一主振型的位移上所做的功，可得

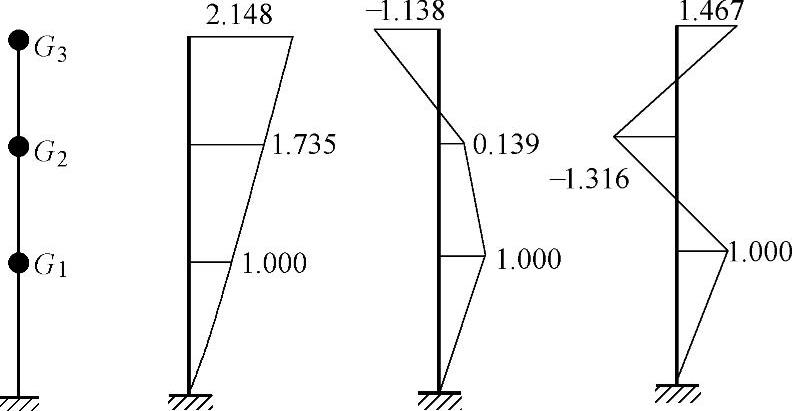
图4.2.7 三质点体系

（m₁ω²₁x₁₁）x₂₁+（m₂ω²₁x₁₂）x₂₂=（m₁ω²₂x₂₁）x₁₁+（m₂ω²₂x₂₂）x₁₂

整理后得（ω²₁-ω²₂）（m₁x₁₁x₂₁+m₂x₁₂x₂₂）=0

由于ω₁≠ω₂，故m₁x₁₁x₂₁+m₂x₁₂x₂₂=0 （4.2.1）

式（4.2.1）所表示的关系，称为主振型的正交性，它反映了主振型的一种特性，即体系各质点的质量与其在两个不同振型上的位移振幅的连乘积的代数和为零。其物理意义是：某一振型在振动过程中所引起的惯性力不在其他振型的位移上做功。这说明某一振型的动能不会转移到其他振型上去，也就是体系按某一振型作自由振动时不会激起该体系其他振型的振动。这也就是前面所说的，如果体系作自由振动时，它的初始位移或初始速度完全符合某一振型时，则体系始终保持按这一振型振动。

（三）多自由度体系j振型的“振子”

利用主振型的正交性，即体系按某一振型作自由振动时不会激起该体系其他振型的振动。可以将一个多自由度体系分解为n个独立非耦联的单自由度体系，求出各个单自由度体系的位移，再通过振型组合，即可求出原体系的位移，从而使得一个复杂的多质点体系振动求解问题得以简化成单自由度体系求解问题。这种解法称“振型分解法”，现通过一个案例的讨论来讲述这种“振型分解法”。(www.xing528.com)

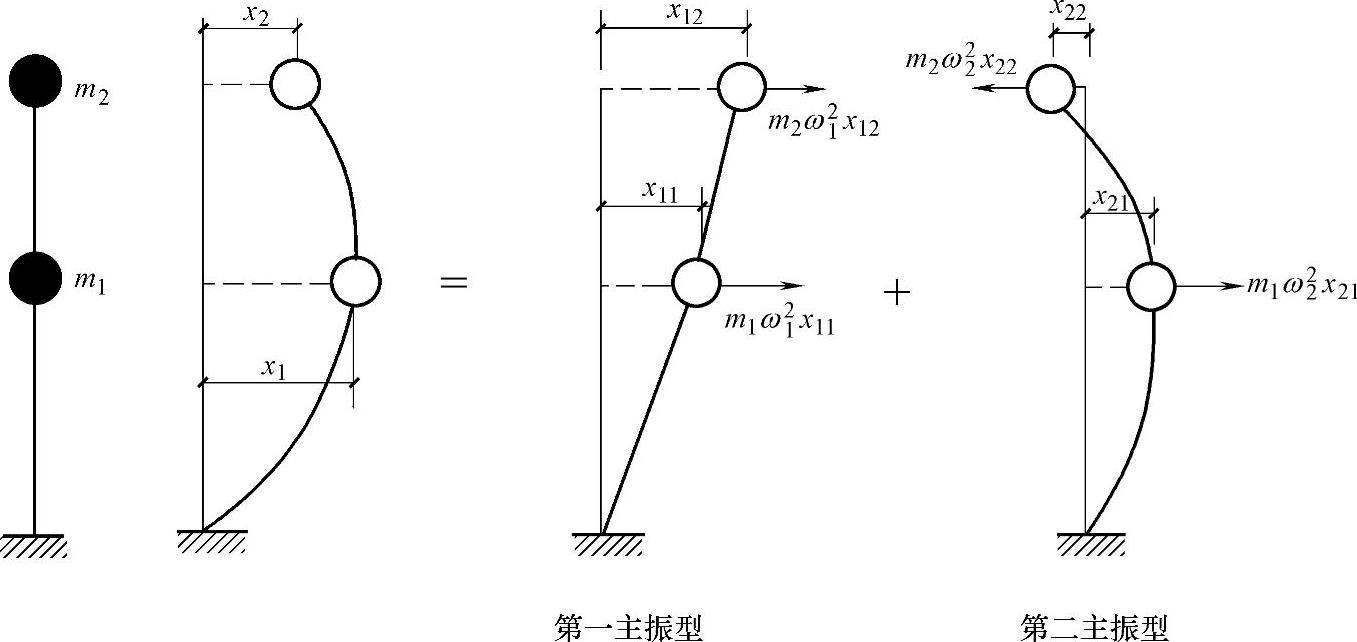
图 4.2.8

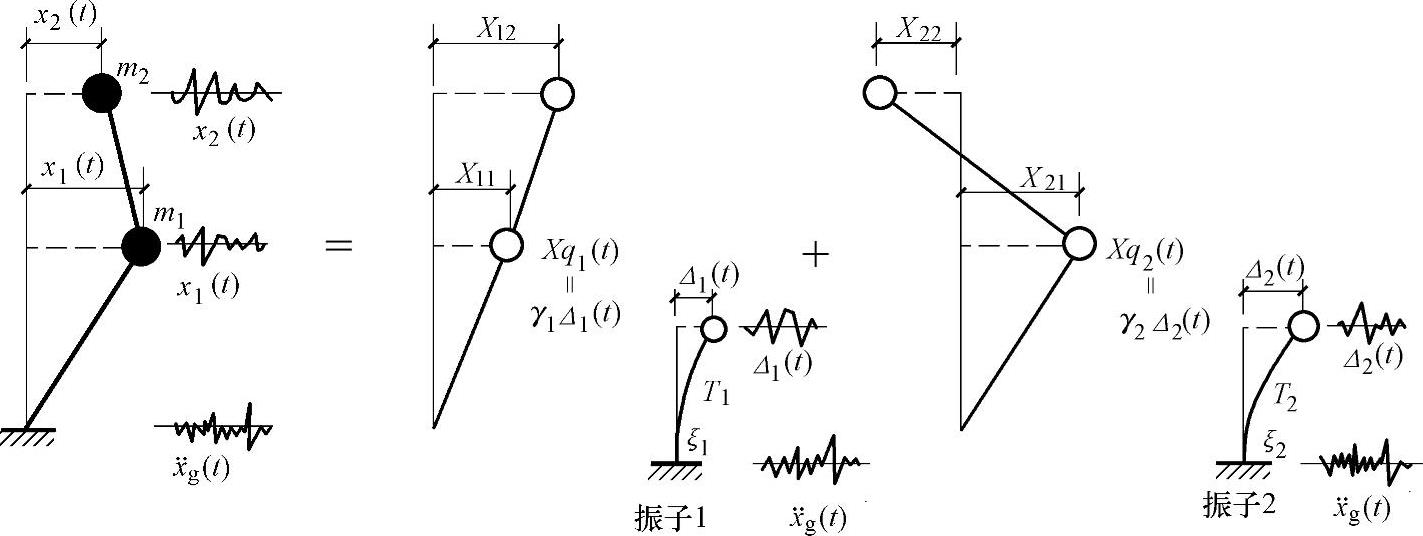
图4.2.9 结构变形按振型分解

为简单起见，仍以两个质点体系为例，如图4.2.9所示。质点m₁及m₂在地震作用下任一时刻的位移x₁（t）和x₂（t）用两个振型的线性组合来表示。为消除耦合作用，引入广义坐标q_j（t），即：

x₁（t）=q₁（t）x₁₁+q₂（t）x₂₁

x₂（t）=q₁（t）x₁₂+q₂（t）x₂₂

对具有n个质点的体系，质点m_i在地震作用下任一时刻的位移x_i（t）表达式为

式中的q₁（t）、q₂（t），表示质点在任一时刻的变位中第一振型与第二振型所占的分量。由于x₁（t）及x₂（t）是时间的函数，所以q₁（t）与q₂（t）也是时间的函数。

为了求得q_j（t），现引入一个如图4.2.10所示的单自由度质点，这个单自由度体系称作与j振型相应的“振子”。这“振子”的阻尼比为ζ_j、自振频率为ω_j。这“振子”在地震作用下的位移反应为Δ_j（t），根据动力学知，存在下列关系：

q_j（t）=γ_jΔ_j（t） （4.2.3）

此处，γ_j称为体系在地震反应中第j振型的振型参与系数。

对具有n个自由度的弹性体系，在地震作用下任一时刻质点m_i的位移x_i（t）计算公式为

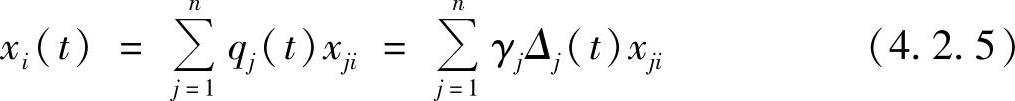
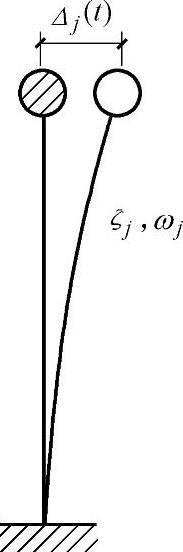
图4.2.10 振子

上式表明，多质点弹性体系质点m_i的地震位移反应等于各振型参与系数与该振型相应的“振子”的地震位移反应的乘积，再乘以该振型质点m_i的相对位移，然后再把它们总和起来。这样，我们就将多质点体系的问题分解为单质点体系来解决了。这种方法不仅对计算多质点体系的地震位移反应十分简便，而且也为按反应谱理论计算多质点体系的地震作用提供了方便条件。