汽车传动系统参数区间方法

如前所述，传动系参数中齿轮齿数和模数为离散变量，而采用以上优化方法获得的速比值是一个确定的最优值，不一定满足生产厂家的实际生产需要，存在着变速器齿轮配齿的问题。为此我们提出了汽车传动系统参数的区间优化模型。在这一模型里，不追求变量的确定优化值，只是在保证一定的优化效果的前提下，求设计变量的最大可行区间，这样就可以扩大传动系参数的选择范围，并可以解决变速器齿轮配齿问题。

用区间数表示需要共享的实际变量，则确定汽车传动系统参数最大可行区间的问题可以表述为扩大设计变量区间数的宽度问题。令X_i为共享设计变量，则求最大共享区间问题的数学模型，即是求最大可行区间问题的数学模型，求最大可行区间宽度的优化问题。在一定的约束条件下，其数学模型为

满足约束条件：

其中，F（…）为约束区间函数；c为约束区间函数的限制值；α_i为加权系数；l为区间变量总数；ω_i（X_i）为第i个区间数的区间宽度；X′_i为可行区间变量X_i的约束区间数，。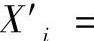

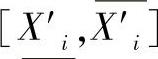上述模型描述的是区间扩张的逆问题，及规定函数的值域区间求定义域区间的问题，在约束函数为凸函数时，有确定的解。

求解上述模型得到的可行区间宽度有时较窄，为了改善效果，引入“条件预优概念及方法”，也就是把影响实值函数F（x₁，x₂，…，x_l，x_l+1，…，x_n）的变量及参数分为两类：其中x₁，x₂，…，x_l为一类，叫作关键变量，我们关心这些变量的可行变化区间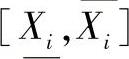，而不关心它们取什么确定值；此外，影响目标函数值的其他变量及参数在一定的范围内变动，这些扩大的变量称为条件变量。

我们采用对条件变量优选的方法，即求x_l+1，x_l+2，…，x_n，以获得minF（x₁，x₂，…，x_l，x_l+1，…，x_n）。

求解模型时，对应于每一组z=[x₁，x₂，…，x_l]^T时，有一组对应的最优变量y^∗=[x^∗_l+1，x^∗_l+2，…，x_n^∗]^T，我们把y^∗称为预优条件变量，把这一类运算成为“条件预优运算”。通过条件预优运算，能明显地提高与改善优化效果，即

F（x₁，x₂，…，x_l，x^∗_l+1，…，x_n^∗）≤F（x₁，x₂，…，x_l，x_l+1，…，x_n）

若把上述预优概念引入模型，那么就可以扩大关键变量允许选取的范围，改善最大可行区间的求解效果。也就是说，在满足性能要求的前提下，扩大关键变量的区域。这样可导出改进的模型如下：(www.xing528.com)

求z=[x₁，x₂，…，x_l]^T，使

求y^∗=[x^∗_l+1，x^∗_l+2，…，x_n^∗]^T，使

其中，X′_j为条件变量的约束区间数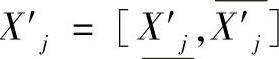，；n为变量总数（包括关键变量和条件变量）。

在具体计算传动系参数最大可行区间问题时，以多工况模式的燃油百公里油耗Q_S为目标区间函数，以满足汽车动力性要求为约束条件。为了简化计算，以传统的按等比级数q来分配变速器各档速比，最高档为直接档；同时取驱动桥速比I₀为另一约束区间数，故约束区间函数可表示为

Q_S（q，I₀）≤c （5-48）

要点

动力传动系统参数的优化，通过发动机性能指标的优选，机械变速器传动比和驱动桥速比的优化，满足在使用工况下的动力传动系统的一系列优化。

本章要点

汽车的主要性能参数是确定汽车性能好坏和特性、特征的指标。在选择中，要依据整车和总成的原始数据和设计目标，进行系统计算分析择优选择确定。