地震作用效应计算方法-钢筋混凝土结构

结构的地震作用效应的动力计算方法主要有：时程动力分析法；振型分解反应谱法；底部剪力法等。

时程动力分析法是将地震波a₀（t）直接输入结构的动力方程求解结构在振动时的位移x（t）。时程动力分析法的计算比较精确，但也比较复杂。振型分解反应谱法及底部剪力法都是动力法中的反应谱法，即按标准的反应谱考虑地震时的地面加速度a₀（t）所引起的结构自身的加速度动力反应，并以作用于结构上的地震惯性力来表示。这样，就将动力问题转化为静力问题处理。振型分解法是综合考虑了结构在不同振型时的地震反应，而底部剪力法只考虑结构第一（基本）振型时的地震反应，因而是一种简化计算方法。

1.底部剪力法

底部剪力法适用于高度不超过40m，以剪切变形为主，且质量与刚度沿高度的分布比较均匀的结构，以及近似于单质点体系的结构（如水塔、单层厂房等）。

（1）单质点体系 图12-4为单层厂房、水塔一类结构。在抗震计算时，其计算简图可简化为支撑在不计质量的弹性杆上的单质点体系，质点的质量为m。当地面水平向加速度为a₀（t）时，质点引发的加速度为a（t）。由牛顿第二定律，可假定在质点上作用有一惯性力F为

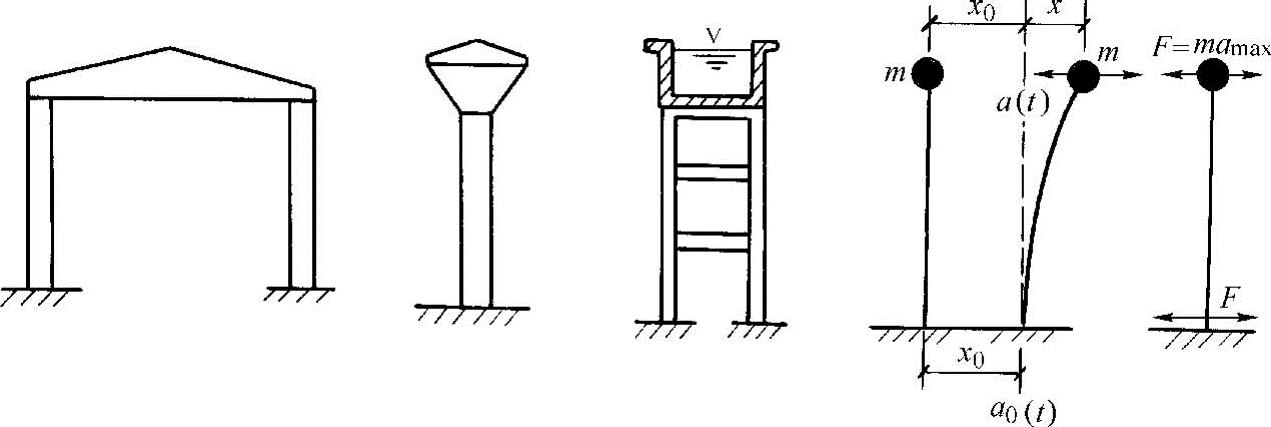
图12-4 单层厂房、水塔类结构简化为单质点体系

F=ma（t） （12-5）

就可将动力问题转化为静力问题处理。

当a（t）=a_max时的惯性力

F=ma_max （12-6）

质点的加速度峰值a_max和地面水平向设计基本地震加速度a_h的大小有关。a_h即为地震设防烈度的定量标准，根据实际地震的分布研究，水平向设计基本地震加速度a_h可按表12-1取值。

质点的加速度峰值a_max和地面水平向设计基本地震加速度a_h之间的关系，可用下式表示：

a_max=βa_h （12-7）

式中 β——动力系数，或称为放大系数。

将式（12-7）中的a_max代入式（12-6），可得出地震惯性力（标准值）

F_k=mβa_h （12-8）

即 F_k=βa_hG/g=α₁G （12-9）

式中 G——质点的总重力荷载代表值，G=mg；

α₁——相应于结构基本自振周期的水平地震影响系数。

由式（12-8）可知，地震作用惯性力和其他外力荷载是不同的。它不仅取决于地震烈度（a_h），还与结构本身的动力特性（自振周期T）及结构的质量（m=G/g）有关。

（2）多质点体系 对于多层框架，抗震计算时的计算简图取为图12-5所示的多质点体系，即将每层的梁、板、柱的质量均集中于楼层处作为一个质点处理。各楼层可仅取一个自由度。n层框架就有n个质点支撑在无质量的弹性直杆上。n个质点体系在振动时就有n个自由度，也就有n个振型。按底部剪力法计算时，只考虑主振型时的质点位移。

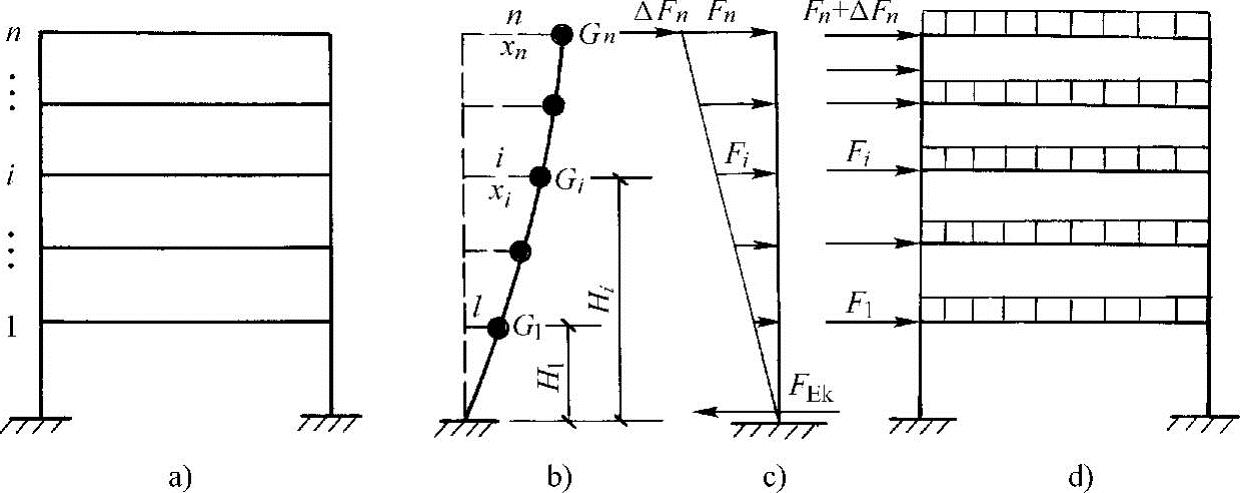
图12-5 多层框架简化为多质点体系

多质点体系受到的结构总水平地震作用标准值F_Ek套用式（12-9）的单质点体系公式，表示为

F_Ek=α₁G_eq （12-10）

式中 G_eq——结构等效总重力荷载。

由于底部剪力法计算多质点体系时，所得地震作用效应将比精确方法计算的偏大15%左右。因此，对多质点体系，就取“等效的”总重力荷载G_eq替代实有的总重力荷载G，G_eq取为0.85G。

对于多质点体系，底部剪力F_Ek求得后，可按倒三角形分布规律，如图12-5c，得出作用于每一质点（每一楼层）上的水平地震作用标准值Fi

式中 G_i、G_j——集中于质点i、j的重力荷载代表值；

H_i、H_j——i、j的计算高度。

由于在振动时，结构顶部会发生“鞭梢效应”，位移x_n将增大许多，由式（12-11）计算出的F_i就比实际作用力偏小，这显然是不安全的，必须加以修正。修正的方法是在顶端质点n处附加一地震力ΔF_n，取ΔF_n=δ_nF_Ek，这样，再根据各质点上的地震力总和（F₁+F₂+…+F_n-1+F_n+ΔF_n）应等于底部剪力F_Ek的条件，可把式（12-11）修正为

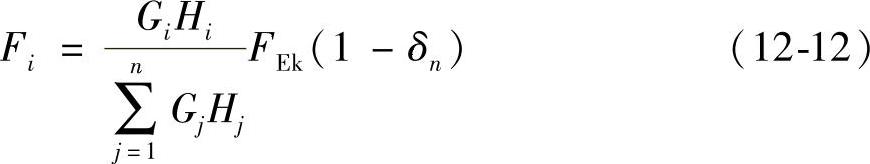
式中 δ_n——顶部附加地震作用系数，对多层钢筋混凝土结构，可按表12-4取用；

ΔF_n——顶部附加水平地震作用。

表12-4 顶部附加地震作用系数δ_n

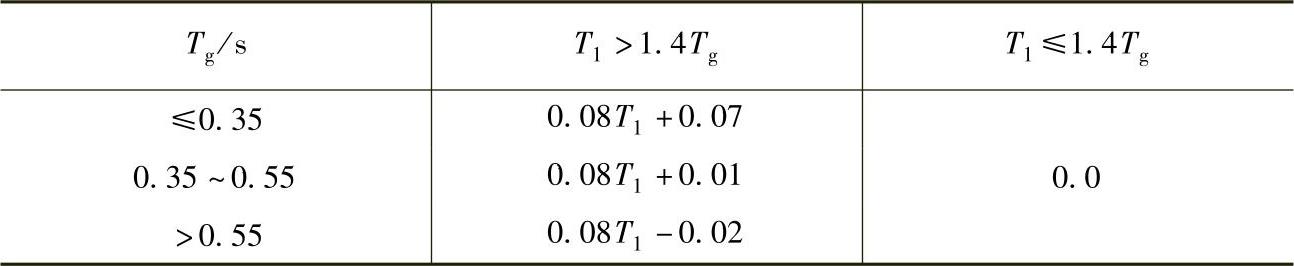
注：T₁为结构基本自振周期。

凸出屋面的屋顶间、女儿墙、烟囱等的地震作用效应，宜乘以增大系数3，此增大部分不应往下传递，但与该凸出部分相连的构件应予计入。

各F_i值得出后，如图12-5d将其加在框架各层上，顶部的地震力为F_n+ΔF_n，再和其他荷载产生的内力相组合，就可得到抗震设计时的结构内力值。

2.振型分解反应谱法

一般高层建筑都要用振型分解反应谱法计算等效地震荷载。

多自由度体系可以按振型分解方法得到多个振型。通常，n层结构可看成n个自由度，有n个振型，如图12-6所示。

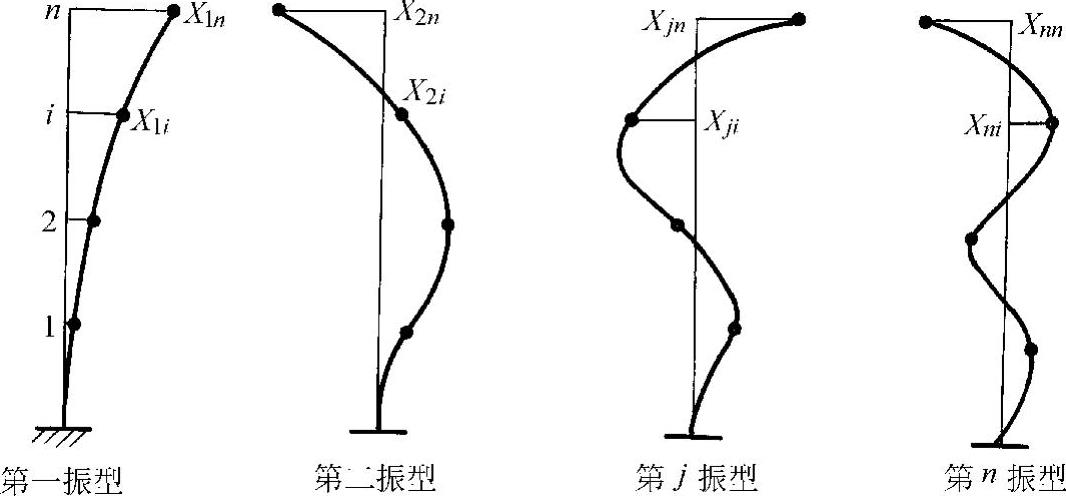
图12-6 振型(www.xing528.com)

采用振型分解反应谱法时，不进行扭转耦联计算的结构，其地震作用和作用效应为：

（1）结构j振型i质点的水平地震作用标准值为

F_ji=α_jγ_jX_jiG_i （i=1.2，…，n，j=1，2，…，m） （12-13）

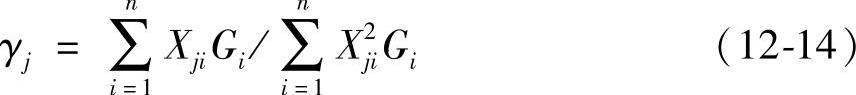
式中 F_ji——j振型i质点的水平地震作用标准值；

α_j——相应于j振型自振周期的地震影响系数；

X_ji——j振型i质点的水平相对位移；

γ_j——j振型的参与系数。

（2）水平地震作用效应（弯矩、剪力、轴向力和变形） 应当特别注意，求出各个振型的等效地震力以后，不能用简单相加得到的总地震力计算内力，而应当用各振型的等效地震力分别计算结构的内力与位移，然后通过振型组合方法计算各个截面的内力及各层位移，振型组合时采用下述公式，称为平方和的平方根方法：

式中 S_Ek——水平地震作用标准值的效应；

S_j——j振型水平地震作用标准值的效应（弯矩、剪力、轴力或是某个楼层的位移）；

m——参加组合的振型数，一般可只取前2～3个振型。当基本自振周期大于1.5s或房屋高宽比大于5时，振型个数应适当增加。

如果要计算作用在该结构上的总的等效地震荷载或底部剪力，也要采用式（12-15）由各振型的等效地震荷载或底部剪力组合得到。这个公式是由概率统计原理推得的，一般，它是作用于结构的最不利等效地震荷载或内力。

用这个方法计算结构的地震作用时，需求出高振型的周期及振幅。突出屋面的屋顶间、女儿墙、烟囱等部分可作为一个质点参加分析。

考虑扭转耦联振型分解法可见参考文献[15]。

抗震验算时，结构任一楼层的水平地震剪力应符合下式要求：

式中 V_Eki——第i层对应于水平地震作用标准值的楼层剪力；

λ——剪力系数，不应小于表12-5规定的楼层最小地震剪力系数值，对竖向不规则结构的薄弱层，尚应乘以1.15的增大系数；

G_j——第j层的重力荷载代表值。

表12-5 楼层最小地震剪力系数值

注：1.基本周期介于3.5s和5s之间的结构，插入法取值；

2.括号内数值分别用于设计基本地震加速度为0.15g和0.30g的地区。

现浇和装配整体式混凝土楼、屋盖等刚性楼盖建筑，宜按抗侧力构件等效刚度的比例分配楼层水平地震剪力。

3.竖向地震作用计算

竖向地震作用一般只在9度地震设防区的高层建筑物和8度、9度地区的大跨度和长悬臂结构中考虑。竖向地震作用会改变墙、柱等构件的轴向力。但在长悬臂及跨度很大的梁中，竖向地震使梁的弯矩和剪力加大的后果也不容忽视。后者在8度及9度设防时，竖向地震作用标准值可分别取该结构、构件重力荷载代表值的10%和20%，设计基本地震加速度为0.30g时，可取该结构、构件重力荷载代表值的15%。

9度时的高层建筑，竖向地震作用引起的竖向地震作用标准值，可以用下述方法计算：

结构总竖向地震作用标准值

F_Evk=α_v，maxG_eq （12-17）

质点i层的竖向地震作用标准值

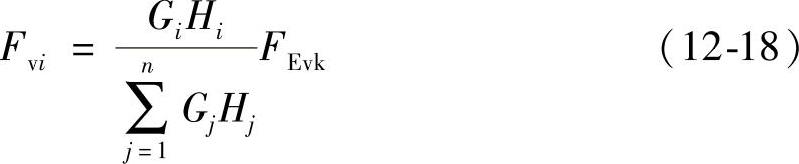
第i层竖向总轴力

式中 α_v，max——竖向地震影响系数的最大值，可取水平地震影响系数最大值的65%；

G_eq——结构等效总重力荷载，取G_eq=0.75G_E，G_E为结构总重力荷载代表值；

G_i（G_j），H_i（H_j）的意义见图12-7。

在求得第i层竖向总轴力后，按各墙、柱所承受的重力荷载值大小，将N_vi分配到各墙、柱上。竖向地震引起的轴力可能为拉、也可能为压，组合时应按不利的值取用。

跨度大于24m屋架的竖向地震作用标准值，宜取其重力荷载代表值和竖向地震作用系数的乘积；竖向地震作用系数可按表12-6采用。

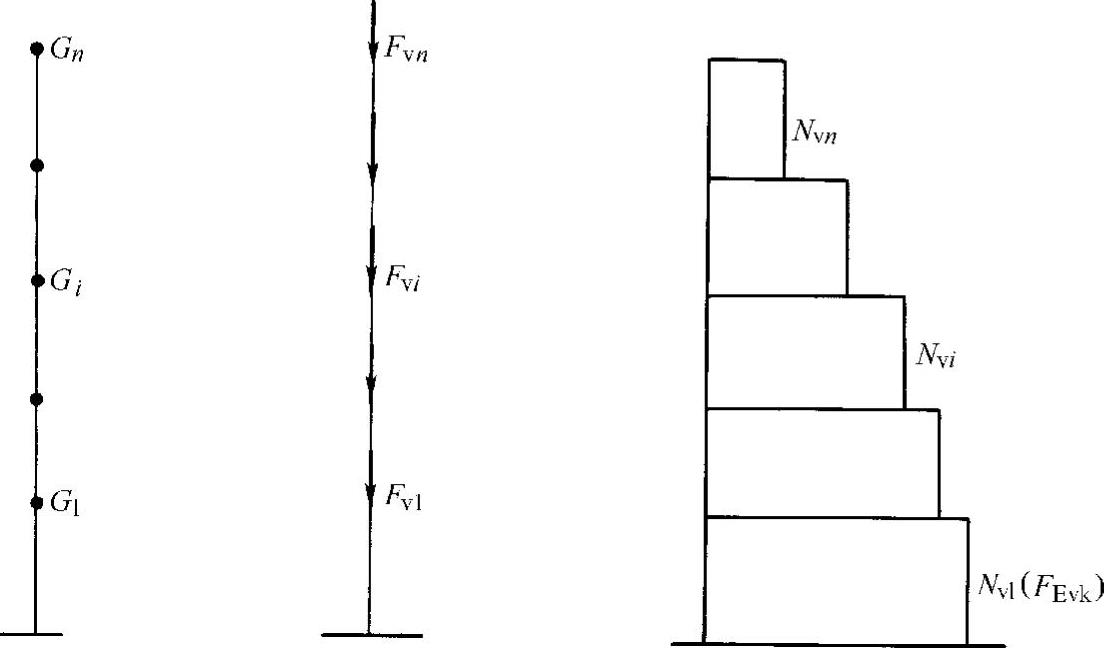
图12-7 竖向地震作用

表12-6 竖向地震作用系数

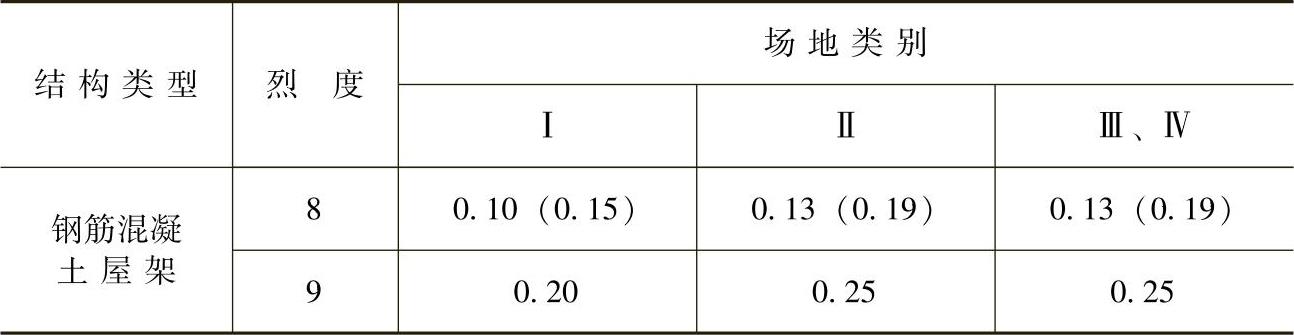
注：括号中数值用于设计基本地震加速度为0.30g的地区。