11.7.1正截面承载力计算-钢筋混凝土结构最新计算方法

试验表明，预应力受弯构件正截面发生破坏时，其截面平均应变符合平截面假定，应力状态如11.6节所述，如符合适筋条件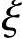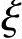（≤_b），计算应力图形如图11-35a。预应力混凝土受弯构件承载力的计算与钢筋混凝土受弯构件基本相同。但由于预应力混凝土受弯构件在加荷前，混凝土和钢筋已处于自相平衡的高应力状态，截面已经有了应变，所以界限破坏时的相对界限受压区高度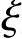_b值不同；另外由于对受压区预应力筋A′_p预先施加了拉应力，所以破坏时受压区预应力筋A′_p的应力σ′_p值为（σ′_p0-f′_py），而达不到其抗压强度设计值f′_py，甚至还可能为拉应力，所以对这两点应特别注意。

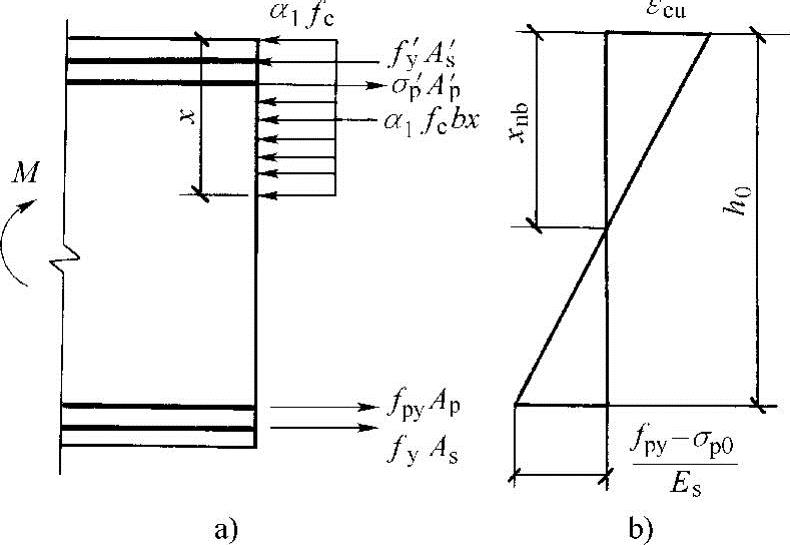
图11-35 界限受压区高度及计算图形

1.相对界限受压区高度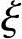_b

对于预应力混凝土受弯构件，相对界限受压区高度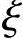_b仍由平截面假定求得。当受拉区预应力筋A_p的合力点处混凝土法向应力为零时，预应力筋中已存在拉应力σ_p0，相应的应变为ε_p0=σ_p0/E_p。从A_p合力点处的混凝土应力为零到界限破坏，预应力筋的应力增加了（f_py-σ_p0），相应的应变增量为（f_py-σ_p0）/E_p。在A_p的应力达到f_py时，受压区边缘混凝土应变也同时达到极限压应变ε_cu。等效矩形应力图形受压区高度与中和轴高度的比值取为β₁。根据平截面假定，由图11-35b所示几何关系，可写出

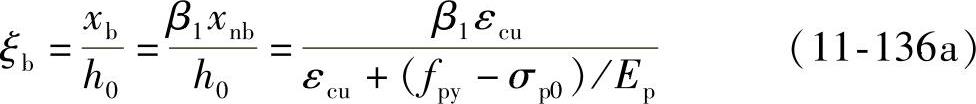
式中 ε_cu——正截面的混凝土极限压应变，按第4章的公式计算，如计算的ε_cu值大于0.0033，取为0.0033。

β₁——系数，当混凝土强度等级不超过C50时，β₁取为0.8，当混凝土强度等级为C80时，β₁取为0.74，其间按线性内插法确定。

对无明显屈服点的钢筋（钢丝和钢绞线），因钢筋达到“协定流限”（σ_0.2）时的应变为ε_py=0.002+f_py/E_p。故式（11-136a）应改为

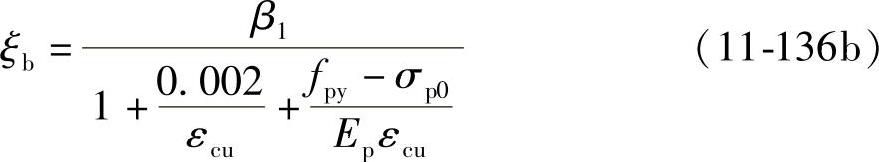
σ_p0为受拉区预应力筋合力点处混凝土法向应力等于零时的预应力筋的应力，先张法σ_p0=σ_con-σ_l，后张法σ_p0=σ_con-σ_l+α_Epσ_pc。

可以看出，预应力构件的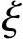_b除与钢材性质有关外，还与预应力值σ_p0大小有关。在截面受拉区内配有不同种类的钢筋或不同的预应力值的受弯构件，其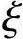_b应分别计算，并取其最小值。

2.预应力筋和普通钢筋的应力

由于受拉区的预应力筋或普通钢筋可能配置几排，在最外排的钢筋屈服后，内排的钢筋可能未屈服，所以需计算钢筋的应力。此时以受压区混凝土边缘达到极限压应变ε_cu作为构件达到承载能力极限状态，而按平截面假定，就可给出截面任意位置处的普通钢筋应力σ_si和预应力筋应力σ_pi。

（1）按平截面假定计算

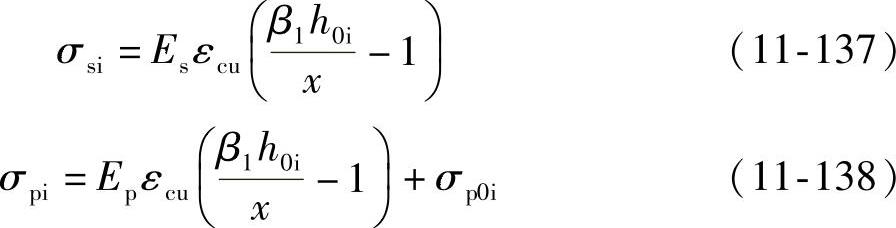
（2）按近似公式计算

为了简化计算，根据我国大量的试验资料及计算分析表明，小偏心受压情况下实测受拉边或受压较小边的钢筋应力σ_s与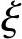接近直线关系。取σ_s与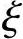之间为线性关系，并考虑到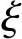=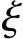_b及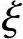=β₁作为界限条件，就可得到

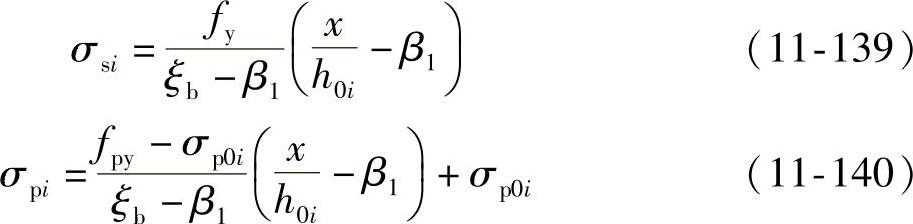
由以上公式求得的钢筋应力应满足下列条件：

-f′_y≤σ_si≤f_y （11-141）

σ_p0i-f′_py≤σ_pi≤f_py （11-142）

当计算的σ_si为拉应力且其值大于f_y时，取σ_si=f_y；当σ_si为压应力且其绝对值大于f′_y时，取σ_si=-f′_y。当计算的σ_pi为拉应力且其值大于f_py时，取σ_pi=f_py；当σ_pi为压应力且其绝对值大于（σ_p0i-f′_py）的绝对值时，取σ_pi=σ_p0i-f′_py。

式中 h_0i——第i层纵向钢筋截面重心至截面受压边缘的距离；

x——等效矩形应力图形的混凝土受压区高度；

σ_si、σ_pi——第i层纵向普通钢筋、预应力筋的应力，正值代表拉应力，负值代表压应力；

f′_y、f′_py——纵向普通钢筋、预应力筋的抗压强度设计值；

σ_p0i——第i层纵向预应力筋截面重心处混凝土法向应力等于零时的预应力筋应力。

3.破坏时受压区预应力筋的应力σ′_p

构件未受到荷载作用前，受压区预应力筋A′_p的拉应变为σ′_pe/E_p。A′_p处混凝土压应变为σ′_pc/E_c。当加荷至受压区边缘混凝土应变达到极限压应变ε_cu时，按规范规定只要满足x≥2a′条件，a′为纵向受压钢筋合力点至受压区边缘的距离，A′_p处混凝土压应变就可达到ε′_c=0.002。则受压区预应力筋A′_p在受压边缘混凝土压碎时的应变为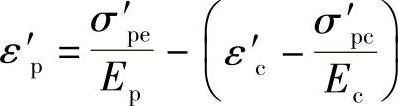，所以σ′_p=ε′_pE_p=σ′_pe+α_Epσ′_pc-ε′_cE_p=σ′p0-α_Epσ′_pc+α_Epσ′_pc-ε′_cE_p=σ′_p0-ε′_cE_p，而ε′_cE_p即为预应力筋的抗压强度设计值f′_py。由此可得

σ′_p=σ′_p0-f′_py （11-143）

式中 σ′_p0为受压区预应力筋A′_p合力点处混凝土法向应力为零时的预应力筋的应力，先张法σ′_p0=σ′_con-σ′_l；后张法σ′_p0=σ′_con-σ′_l+α_Epσ′_pc。

由式（11-143）可见，当σ′_p0>f′_py时，则在破坏时，σ′_p仍为拉应力；当σ′_p0<f′_py时，则在破坏时σ′_p为压应力，但此压应力小于f′_py。因此，与普通钢筋混凝土受弯构件比较，对受压区钢筋施加预应力会使构件截面的承载力降低。配置A′_p后，也减弱了使用阶段的截面抗裂性。因此，在预压时构件上边缘不出现裂缝或允许出现裂缝，但裂缝宽度在允许范围内时，不要配置受压区预应力筋。

4.正截面承载力计算公式

预应力混凝土受弯构件正截面受弯承载力计算公式可由内力平衡条件求得。

（1）矩形截面

配有预应力筋A_p、A′_p，普通钢筋A_s及A′_s的矩形截面受弯构件简图如图11-36所示，和普通钢筋混凝土构件一样，混凝土中的压应力采用等效矩形应力分布。其计算公式如下：

α₁f_cbx=f_yA_s-f′_yA′_s+f_pyA_p+（σ′_p0-f′_py）A′_p （11-144）

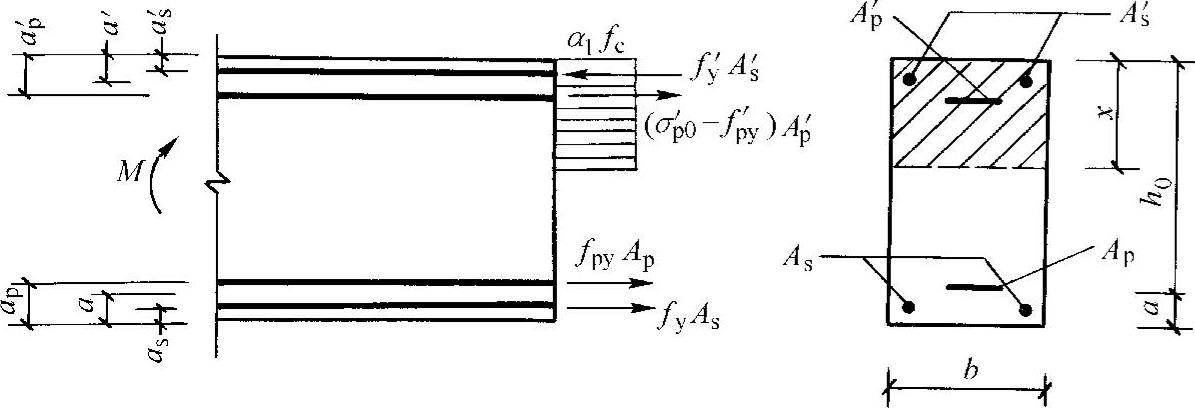
图11-36 矩形截面受弯构件正截面受弯承载力计算(www.xing528.com)

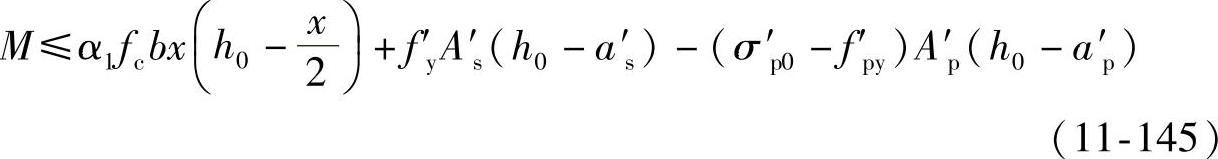
公式的适用条件：

x≤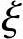_bh₀； x≥2a′ （11-146）

式中 M——弯矩设计值；

f_c——混凝土轴心抗压强度设计值；

α₁——系数，当混凝土强度等级不超过C50时，α₁取为1；当混凝土强度等级为C80时，α₁取为0.94，其间按线性内插法确定；

A_s、A′_s——受拉区、受压区纵向普通钢筋的截面面积；

A_p、A′_p——受拉区、受压区纵向预应力筋的截面面积；

h₀——截面的有效高度，h₀=h-a；

a——受拉区预应力和普通钢筋合力点到截面受拉边缘的距离；

b——矩形截面的宽度；

a′_s、a′_p——受压区纵向普通钢筋合力点、受压区纵向预应力筋合力点至受压边缘的距离；

σ′_p0——受压区纵向预应力筋合力点处混凝土法向应力为零时，受压区纵向预应力筋的应力；

a′——受压区全部纵向钢筋合力点至截面受压区边缘的距离，当受压区未配置纵向预应力筋或受压区纵向预应力筋的应力（σ′_p0-f′_py）为拉应力时，a′应用a′_s代替；

f_y、f_py——受拉区纵向普通钢筋、纵向预应力筋抗拉强度设计值；

f′_y、f′_py——受压区纵向普通钢筋、纵向预应力筋抗压强度设计值；x——受压区计算高度。

应注意，当截面受拉区内即配置纵向预应力筋又配置普通钢筋时，应根据预应力筋及普通钢筋分别求出相对界限受压区高度，并取其较小值。

当x<2a′时，正截面受弯承载力可按下式计算：

M≤f_pyA_p（h-a_p-a′_s）+f_yA_s（h-a_s-a′_s）+（σ′_p0-f′_py）A′_p（a′_p-a′_s） （11-147）

式中 a_s，a_p——受拉区纵向普通钢筋、受拉区纵向预应力筋至受拉边缘的距离。

（2）翼缘位于受压区的T形截面及Ⅰ字形截面

和普通混凝土受弯构件一样，对于T形截面构件，进行正截面受弯承载力计算时，应首先判别属于哪一类T形截面（图11-37）。

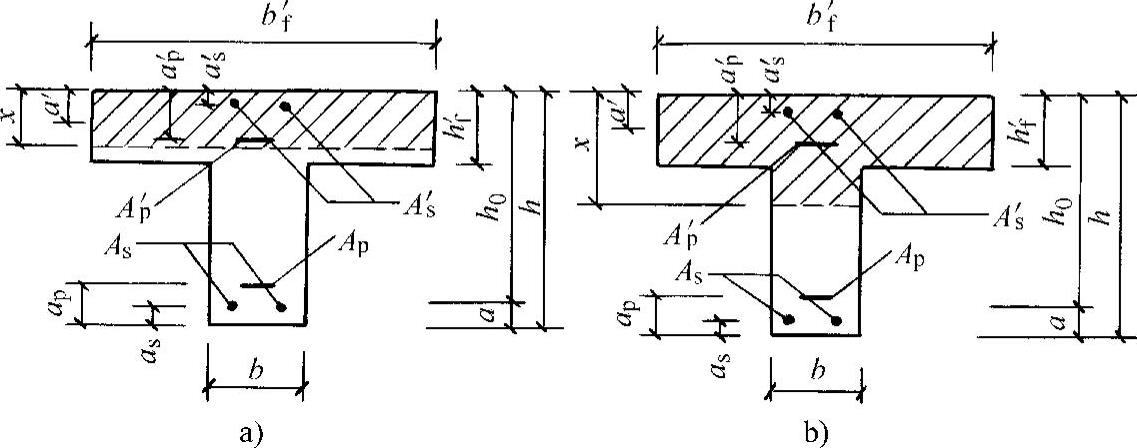
图11-37 T形截面受弯构件受压区高度位置

截面设计时，

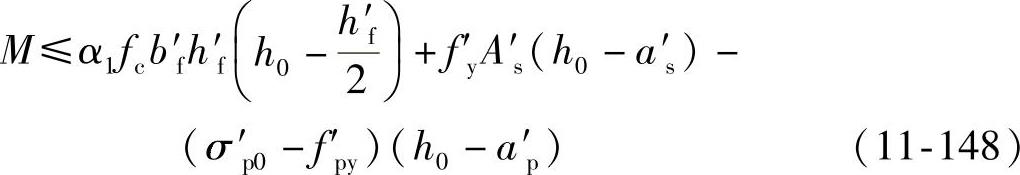
截面复核时，

f_yA_s+f_pyA_p≤α₁f_cb′_fh′_f+f′_yA′_s-（σ′_p0-f′_py）A′_p （11-149）

为第一类T形截面，按截面宽度为b′_f的矩形截面计算。

当不符合式（11-148）、式（11-149）条件时，为第二类T形截面，即x>h′_f，中和轴通过肋部，按下列公式计算：

α₁f_c[bx+（b′_f-b）h′_f]=f_yA_s-f′_yA′_s+f_pyA_p+（σ′_p0-f′_py）A′_p （11-150）

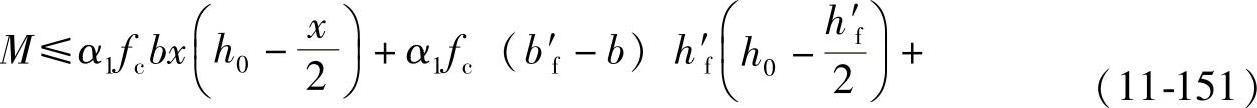
f′_yA′_s（h₀-a′_s）-（σ′_p0-f′_py）A′_p（h₀-a′_p）

式中 h′_f——T形截面受压区的翼缘高度；

b′_f——T形截面受压区的翼缘计算宽度；

其余符号意义同前。

混凝土的受压区高度x应满足式（11-146）要求。如x<2a′，正截面受弯承载力可按式（11-147）计算。此外，无论矩形截面还是T形截面，纵向受力钢筋（A_p+A_s）的百分率还应满足最小配筋率要求。

当由构造要求或按正常使用极限状态验算要求配置的纵向受拉钢筋截面面积大于受弯承载力要求的配筋面积时，按式（11-144）或式（11-150）计算的混凝土受压区高度x，可仅计入受弯承载力条件所需的纵向受拉钢筋截面面积。