11.6.1先张法受弯构件应力分析姜学浩

先张法受弯构件从张拉钢筋开始直到破坏为止的整个应力变化情况，与轴心受拉构件完全类似，可分为6种应力状态（见表11-9）。

表11-9 预应力混凝土受弯构件各阶段的应力状态

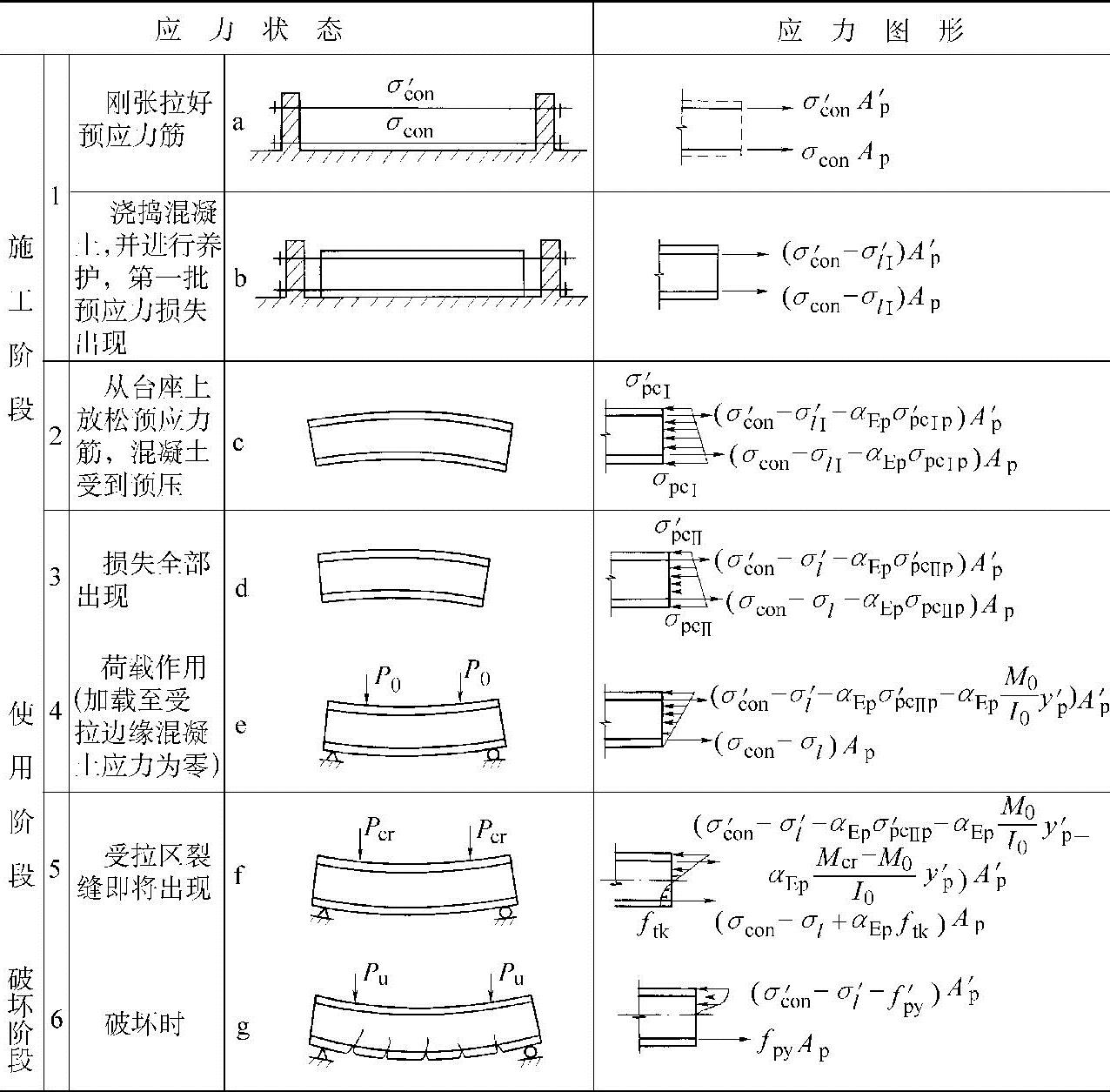
注：为清晰起见，图中未表示出普通钢筋A_s、A′_s及其应力。

1.施工阶段

施工阶段包括三种应力状态。

（1）应力状态1——放松预应力筋前（表11-9图a、b）。张拉钢筋时，预应力筋A_p的控制应力为σ_con，A′_p的控制应力为σ′_con。当第一批预应力损失出现后，钢筋张拉力分别为（σ_con-σ_lⅠ）A_p及（σ′_con-σ′_lⅠ）A′_p。预应力筋和普通钢筋的合力N_p0Ⅰ（此时非预应力筋应力为零）为

N_p0Ⅰ=（σ_con-σ_lⅠ）A_p+（σ′_con-σ′_lⅠ）A′_p （11-89）

它由台座（或钢模）支承平衡。在此状态，混凝土尚未受到压缩，应力为零。

（2）应力状态2——放松预应力筋（表11-9图c）。在从台座（或钢模）上放松预应力筋时，预应力筋的总拉力N_p0Ⅰ反过来作用在混凝土截面上一偏心压力，使混凝土产生法向应力。由于出现裂缝之前，预应力筋与混凝土粘结在一起共同变形，所以可把N_p0Ⅰ视为外力，作用在换算截面A₀上，按偏心受压公式计算截面下、上各点的混凝土法向应力。

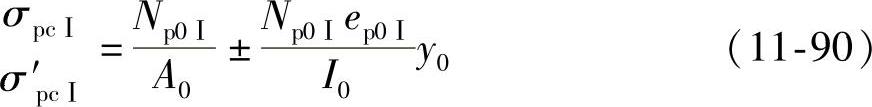
式中 A₀——换算截面面积，A₀=A_c+α_EpA_p+α_EsA_s+α_EpA′_p+α_EsA′_s；

A_c——混凝土截面面积；

I₀——换算截面A₀的惯性矩；

e_p0Ⅰ——预应力筋和普通钢筋合力N_p0Ⅰ至换算截面重心轴的距离；

y₀——换算截面重心轴至所计算的纤维层的距离。

偏心力N_p0Ⅰ的偏心距e_p0Ⅰ可按下式求得：

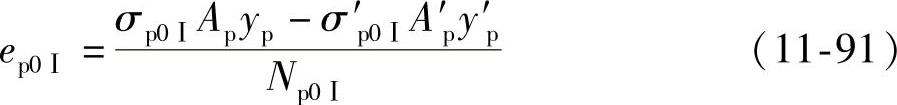
式中 σ_p0Ⅰ、σ′_p0Ⅰ——放张前下、上预应力筋的拉应力，σ_p0Ⅰ=σ_con-σ_lⅠ、σ′_p0Ⅰ=σ′_con-σ_lⅠ；

y_p、y′_p——受拉区、受压区预应力筋各自合力点至换算截面重心轴的距离。

在利用式（11-90）求换算截面重心轴以下和以上各点混凝土预应力值时，对公式右边第二项前分别取相应的正号和负号，所求得的混凝土预应力值以压应力为正。

此时，相应的上、下预应力筋的应力（拉应力，且为正）和上、下普通钢筋的应力（压应力，且为正）分别为

σ′_peⅠ=（σ′_con-σ′_lⅠ）-α_Epσ′_pcⅠp=σ′_p0Ⅰ-α_Epσ′_pcⅠp （11-92）

σ_peⅠ=（σ_con-σ_lⅠ）-α_Epσ_pcⅠp=σ_p0Ⅰ-α_Epσ_pcⅠp （11-93）

σ′_sⅠ=α_Esσ′_pcⅠs （11-94）

σ_sⅠ=α_Esσ_pcⅠs （11-95）

上列式中σ′_pcⅠp、σ_pcⅠp和σ′_pcⅠs、σ_pcⅠs分别为第一批损失出现后A′_p、A_p和A′_s、A_s重心处混凝土法向应力值。它们可由式（11-90）求出，只要将式中的y₀分别代以y′_p、y_p及y′_s、y_s。σ′_pcⅠp、σ_pcⅠp用于求σ′_l5、σ_l5。

（3）应力状态3——第二批预应力损失完成后（表11-9图d）。先张法第二批损失仅为混凝土收缩与徐变引起的预应力损失。这一损失不仅对预应力筋的应力有影响，同时对普通钢筋的应力也有影响。当预应力筋合力点处混凝土法向应力为零时，预应力筋和普通钢筋的合力N_p0Ⅱ为：

N_p0Ⅱ=（σ_con-σ_l）A_p+（σ′_con-σ′_l）A′_p-σ_l5A_s-σ′_l5A′_s （11-96）

在N_p0Ⅱ作用下，截面下、上各点的混凝土法向应力为

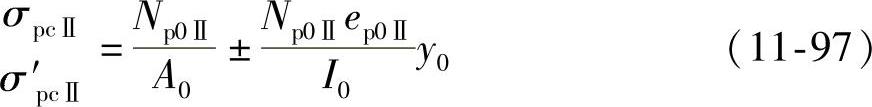(www.xing528.com)

N_p0Ⅱ至换算截面重心轴的偏心距e_p0Ⅱ可按下式求得

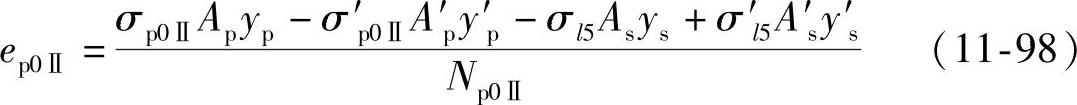
式中 σ′_p0Ⅱ、σ_p0Ⅱ——第二批预应力损失出现后，当混凝土法向应力

为零时，上、下预应力筋的拉应力，σ′_p0Ⅱ=（σ′_con-σ′_l）、σ_p0Ⅱ=（σ_con-σ_l）；

y_s、y′_s——受拉区、受压区普通钢筋各自合力点至换算截面重心轴的距离。

相应的下、上预应力筋的拉应力和普通钢筋的压应力为

σ_peⅡ=（σ_con-σ_l）-α_Epσ_pcⅡp=σ_p0Ⅱ-α_Epσ_pcⅡp （11-99）

σ′_peⅡ=（σ′_con-σ′_l）-α_Epσ′_pcⅡp=σ′_p0Ⅱ-α_Epσ′_pcⅡp （11-100）

σ_sⅡ=σ_l5+α_Esσ_pcⅡs （11-101）

σ′_sⅡ=σ′_l5+α_Esσ′_pcⅡs （11-102）

式中 σ′_pcⅡp、σ_pcⅡp和σ′_pcⅡs、σ_pcⅡs值可由式（11-97）求得。

2.使用阶段

使用阶段包括二种应力状态。

（4）应力状态4——加荷至消压弯矩（表11-9图e）。外荷载逐渐增加至在截面下边缘产生的拉应力刚好抵消下边缘混凝土的预压应力。此时的弯矩称为消压弯矩M₀，其值为

M₀=σ_pcⅡW₀ （11-103）

式中 W₀——换算截面对受拉边缘的弹性抵抗矩，W₀=I₀/y。

此时下上预应力筋的拉应力σ_p0、σ′_p0分别由σ_peⅡ增加α_Ep（M₀/I₀）y_p和由σ′_peⅡ减少α_Ep（M₀/I₀）y′_p，即

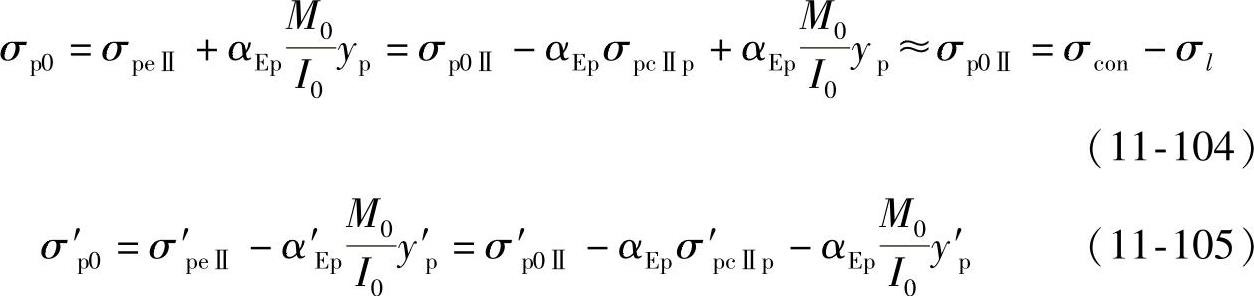
相应的下、上普通钢筋的压应力σ_s0、σ′_s0则分别由σ_sⅡ减少α_Es（M₀/I₀）y_s和由σ′_sⅡ增加α_Es（M₀/I₀）y′_s，即

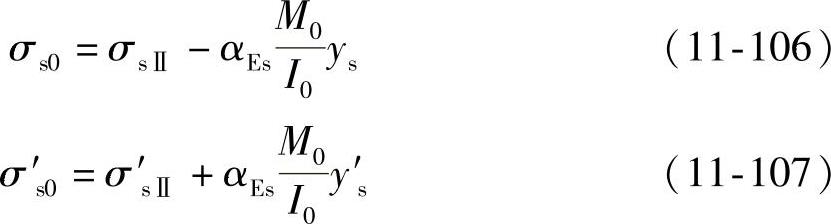
（5）应力状态5——截面下边缘混凝土即将出现裂缝的应力状态（表11-9图f）。如外荷载继续增加至M>M₀，则截面下边缘混凝土将转化为受拉。当混凝土拉应力达到混凝土轴心抗拉强度标准值f_tk时，混凝土即将出现裂缝。此时截面上受到的弯矩即为开裂弯矩M_cr

M_cr=M₀+f_tkW₀=（σ_pcⅡ+f_tk）W₀ （11-108）

在裂缝即将出现的瞬间，受拉区预应力筋的拉应力由σ_p0近似增加α_Epf_tk（因f_tk为截面下边缘混凝土的应力，而预应力筋距下边缘的距离为a_p，所以增加的应力要小于α_Epf_tk），从而得

σ_pcr=σ_p0+α_Epf_tk≈σ_p0Ⅱ+α_Epf_tk （11-109）

而受压区预应力钢筋的拉应力则由σ′_p0减少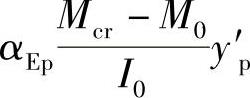，即

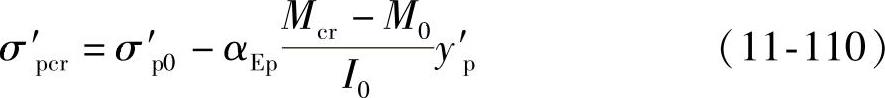
此时，相应的下、上普通钢筋的压应力σ_scr、σ′_scr则分别由σ_s0减少α_Esf_tk和由σ′_s0增加α_Es（（M_cr-M₀）/I₀）y′_s。

此状态为预应力混凝土受弯构件抗裂验算的应力计算模型和理论依据。

3.破坏阶段

（6）应力状态6——加荷至构件破坏（表11-9图g）。当外荷载继续增大至M>M_cr，受拉区出现裂缝，裂缝截面受拉混凝土退出工作，全部拉力由钢筋承担。当外荷载增大至构件破坏时，截面受拉区预应力筋和普通钢筋的应力先达到屈服强度，然后受压区边缘混凝土应变达到极限压应变，致使混凝土压碎，构件达到极限承载力。此时，受压区普通钢筋的应力可达到受压屈服强度。而预应力筋的应力σ′_p可能是拉应力，也可能是压应力，但不可能达到f′_py，详见11.7节。