预应力损失与钢筋混凝土结构

预应力筋在张拉时所建立的预拉应力，会由于张拉工艺和材料特性等种种原因而降低，这种预应力降低的现象称为预应力损失。能否正确预计预应力损失并设法减少预应力损失是保证预应力构件质量的关键。预应力损失可分为下列几种：

1.张拉端锚具变形和预应力筋内缩引起的预应力损失σ_l1

预应力筋张拉至控制应力值后，用锚具加以锚固，由于锚具的变形（如螺杆锚具的垫板间缝隙的挤紧，预应力筋在锥形锚具中的滑动等等）和预应力筋内缩使得拉紧的预应力筋内缩a（mm）值。预应力筋内缩，应力就有所降低，所引起的预应力损失等于：

式中 l——张拉端至锚固端之间的距离（mm）；

E_s——预应力筋的弹性模量；

a——张拉端锚具变形和预应力筋内缩值（mm），见表11-1。

表11-1 锚具变形和预应力筋内缩值a （mm）

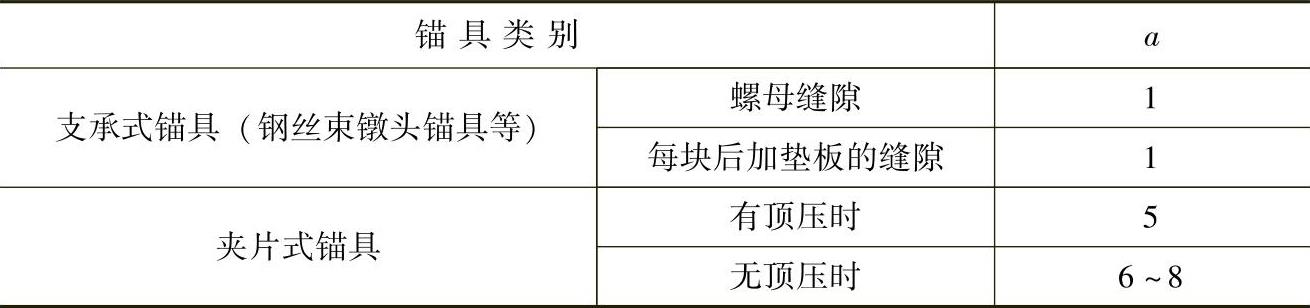
注：1.表中的锚具变形和预应力筋内缩值也可根据实测数据确定；

2.其他类型的锚具变形和预应力筋内缩值应根据实测数据确定。

块体拼成的结构，其预应力损失尚应计及块体间填缝的预压变形。当采用混凝土或砂浆为填缝材料时，每条填缝的预压变形值可取为1mm。

式（11-1）仅适用于直线预应力筋。对于后张法构件曲线预应力筋或折线预应力筋，由于锚具变形和预应力筋内缩引起的预应力损失值σ_l1，应根据曲线预应力筋或折线预应力筋与孔道壁之间反向摩擦影响长度l_f范围内的预应力筋变形值等于锚具变形和预应力筋内缩值的条件确定，反向摩擦系数可按表11-2采用。

表11-2 摩擦系数

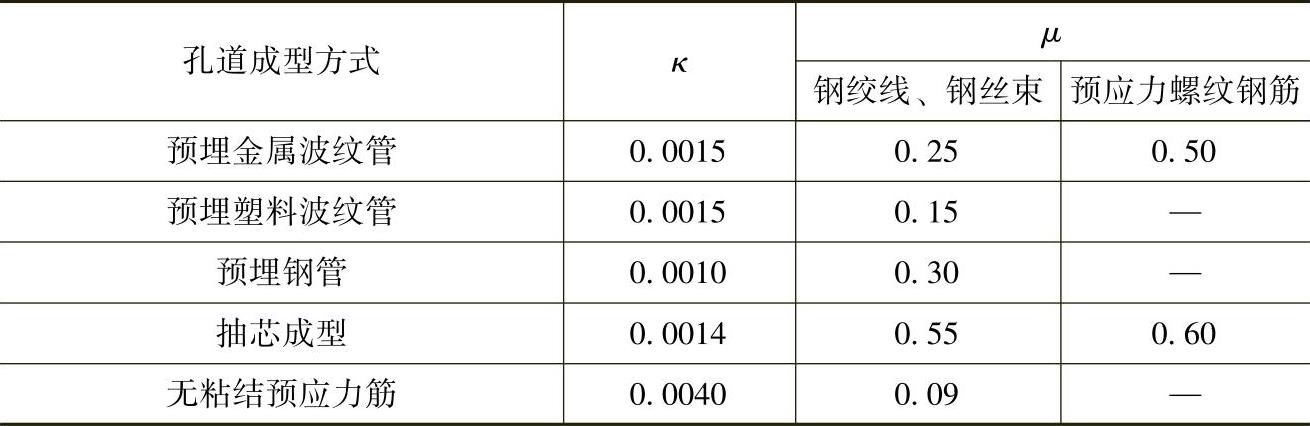
注：摩擦系数也可根据实测数据确定。

当预应力筋为圆弧形曲线（抛物线形预应力钢筋也可近似按圆弧形曲线预应力筋考虑），且其对应的圆心角θ≤45°时（图11-21），对无粘结预应力筋θ≤90°，由于锚具变形和钢筋内缩，在反向摩擦影响长度l_f范围内的预应力损失值σ_l1可按下列公式计算：

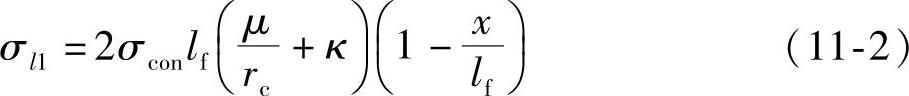
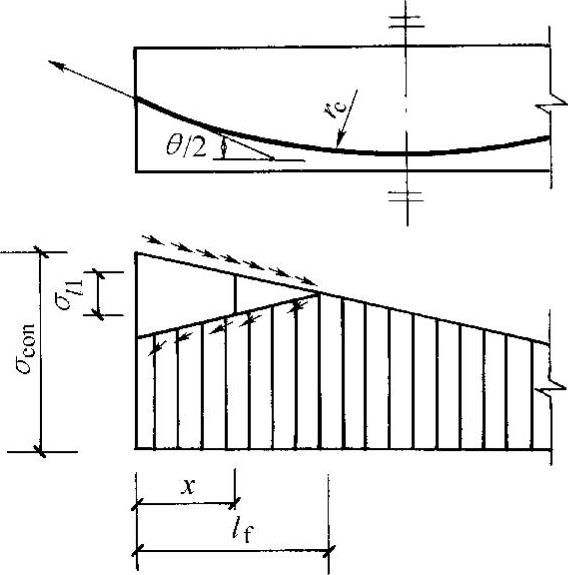
图11-21 圆弧形曲线预应力 钢筋的预应力损失σl1

反向摩擦影响长度l_f（m）可按下列公式计算：

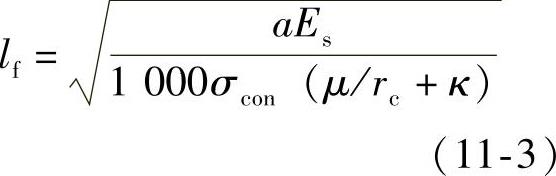
式中 r_c——圆弧形曲线预应力筋的曲率半径（m）；

μ——预应力钢筋与孔道壁之间的摩擦系数，按表11-2采用；

κ——考虑孔道每米长度局部偏差的摩擦系数，按表11-2采用；

x——张拉端至计算截面的距离（m）；

a——张拉端锚具变形和预应力筋内缩值（mm），按表11-1采用；

E_s——预应力筋弹性模量。

端部为直线（直线长度为l₀），而后由两条圆弧形曲线（圆弧对应的圆心角θ≤45°，对无粘结预应力筋取θ≤90°）组成的预应力筋（图11-22），由于锚具变形和钢筋内缩，在反向摩擦影响长度l_f范围内的预应力损失值σ_l1可按下列公式计算：

当x≤l₀时

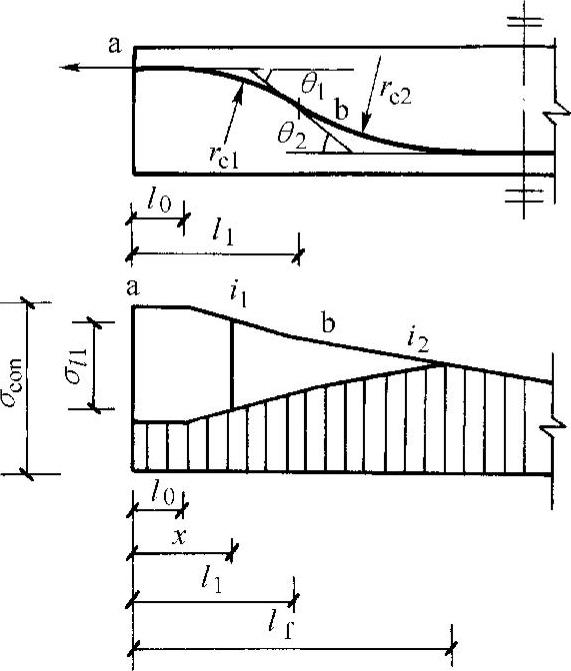
图11-22 两条圆弧形曲线组成的预应力筋的预应力损失σ_l1

σ_l1=2i₁（l₁-l₀）+2i₂（l_f-l₁） （11-4）

当l₀<x≤l₁时

σ_l1=2i₁（l₁-x）+2i₂（l_f-l₁） （11-5）

当l₁<x≤l_f时

σ_l1=2i₂（l_f-x） （11-6）

反向摩擦影响长度l_f（m）可按下列公式计算：

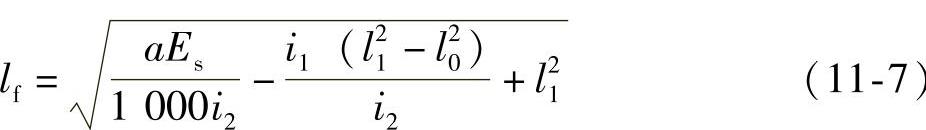
i₁=σ_a（κ+μ/r_c1） （11-8）

i₂=σ_b（κ+μ/r_c2） （11-9）

式中 l₁——预应力筋张拉端起点至反弯点的水平投影长度；

i₁、i₂——第一、二段圆弧形曲线预应力筋中应力近似直线变化的斜率；

r_c1、r_c2——第一、二段圆弧形曲线预应力筋的曲率半径；

σ_a、σ_b——预应力筋在a、b点的应力。

当折线形预应力筋的锚固损失消失于折点c之外时（图11-23），由于锚具变形和预应力筋内缩，在反向摩擦影响长度l_f范围内的预应力损失值σ_l1可按下列公式计算：

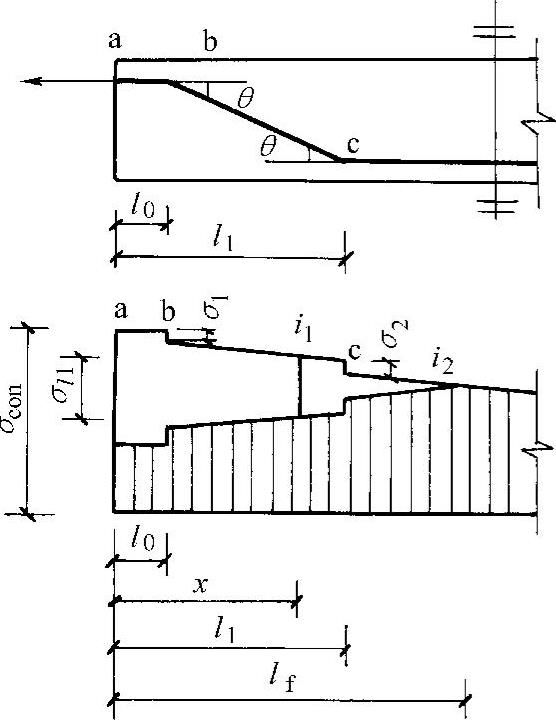
图11-23 折线形预应力钢筋的预应力损失σ_l1

当x≤l₀时

σ_l1=2σ₁+2i₁（l₁-l₀）+2σ₂+2i₂（l_f-l₁） （11-10）

当l₀<x≤l₁时

σ_l1=2i₁（l₁-x）+2σ₂+2i₂（l_f-l₁） （11-11）

当l₁<x≤l_f时

σ_l1=2i₂（l_f-x） （11-12）

反向摩擦影响长度l_f（m）可按下列公式计算：

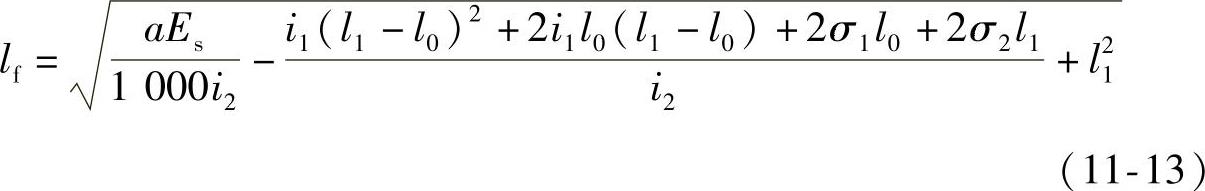
i₁=σ_con（1-μθ）κ （11-14）

i₂=σ_con[1-κ（l₁-l₀）]（1-μθ）2κ （11-15）

σ₁=σ_conμθ （11-16）

σ₂=σ_con[1-κ（l₁-l₀）]（1-μθ）μθ （11-17）

式中 i₁——预应力筋在bc段中应力近似直线变化的斜率；

i₂——预应力筋在折点c以外应力近似直线变化的斜率；

l₁——张拉端起点至预应力筋折点c的水平投影长度。

减小锚具变形和预应力筋内缩引起的预应力损失σ_l1的措施有：

（1）选择锚具变形、预应力回缩量小的锚具、夹具；

（2）尽量减少垫板的块数，因每增加一块垫板，a值增加1mm；

（3）对于先张法构件可增加台座长度l（几个构件通长布置，采用通长的预应力筋）。

2.预应力筋与孔道壁之间的摩擦引起的预应力损失值σ_l2

后张法张拉钢筋时，预应力筋与混凝土孔道壁之间有摩擦力存在，这主要是由于预留孔道的偏差及孔道壁表面粗糙引起的。在曲线段，预应力筋对孔道壁还产生垂直于孔壁的压力，从而增大了摩擦力。由于摩擦力的影响，从张拉端开始，每一截面上的预应力筋的实际预拉应力是逐渐减小的。这种应力差额就是摩擦引起的预应力损失，用σ_l2表示。σ_l2宜按下列公式计算（图11-24）。

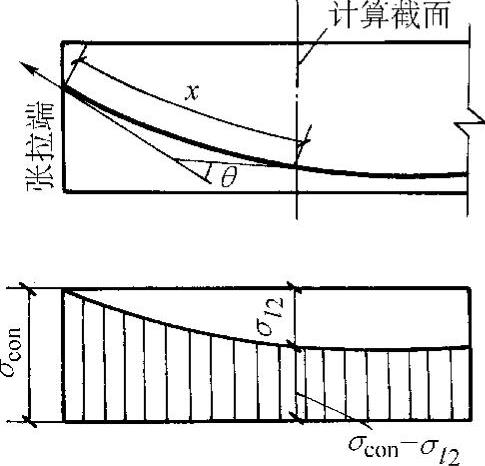
图11-24 摩擦损失示意图

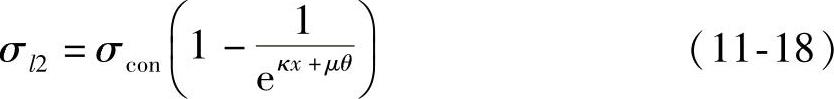
当（κx+μθ）不大于0.3时，σ_l2可按下列近似公式计算：

σ_l2=（κx+μθ）σ_con （11-19）

式中 x——从张拉端至计算截面的孔道长度（m），可近似取该段孔道在纵轴上的投影长度（图11-24）；

θ——从张拉端至计算截面曲线孔道各部分切线的夹角之和（rad）。

在式（11-18）中，对按抛物线、圆弧曲线变化的空间曲线及可分段后叠加的广义空间曲线，夹角之和θ可按下列近似公式计算：

抛物线、圆弧曲线：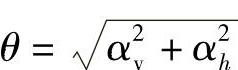

广义空间曲线：

式中 α_v、α_h——按抛物线、圆弧曲线变化的空间曲线预应力筋在竖直向、水平向投影所形成抛物线、圆弧曲线的弯转角；

Δα_v、Δα_h——广义空间曲线预应力筋在竖直向、水平向投影所形成分段曲线的弯转角增量。

先张法构件当采用折线预应力筋时，应考虑加设转向装置处引起的摩擦损失，其值应按实际情况确定。

减小摩擦损失σ_l2的措施有：

（1）两端张拉 由图11-25a、b可知，两端张拉比一端张拉可减小1/2摩擦损失值（当构件长度超过18m或较长构件的曲线式配筋常采用两端张拉的施工方法），但增加了锚具变形引起的损失σ_l1，所以这两者要综合平衡考虑。

（2）超张拉 如图11-25c所示，其张拉顺序为：先使张拉端钢筋应力由（0→1.05）σ_con（A点到E点），持荷2min，再卸荷使张拉应力退到0.85σ_con（E点到F点），持荷2min，再加荷使张拉应力达到σ_con（F点到C点）这样可使摩擦损失（特别在端部曲线部分处）减小，比一次张拉到σ_con的预应力分布更均匀，见CGHD曲线。

3.受张拉的预应力筋与承受拉力的设备之间的温差引起的预应力损失σ_l3

对于先张法构件，预应力筋在常温下张拉并锚固在承受拉力的设备上，如为了缩短生产周期，浇筑混凝土后常进行蒸汽养护。在养护的升温阶段，预应力筋因温度升高而伸长，因而预应力筋的部分弹性变形就转化为温度变形，预应力筋的拉紧程度就有所变松，张拉应力就有所减小，形成预应力损失。在降温时混凝土与预应力筋已粘结成整体，能够一起回缩，由于这两种材料的膨胀系数相近，相应的应力就不再变化。σ_l3仅在先张法中存在。

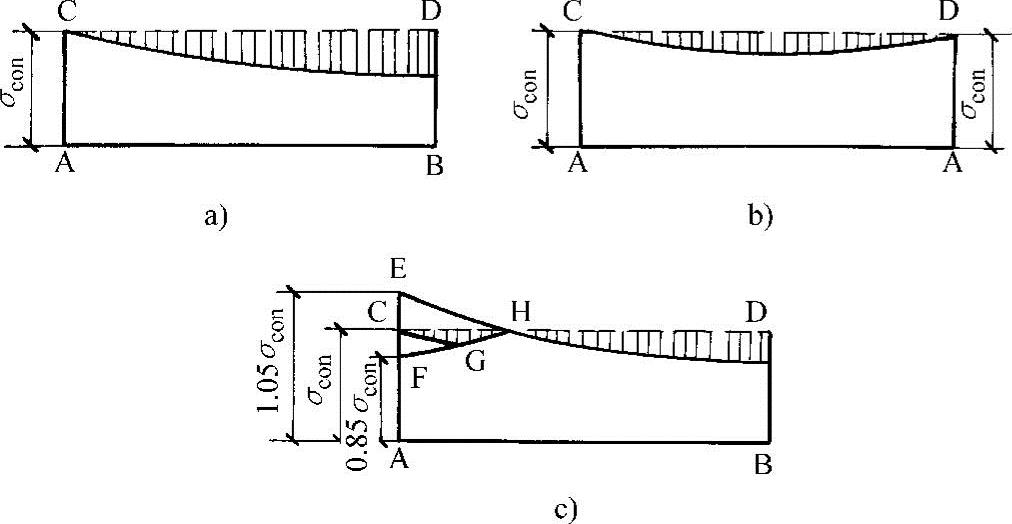
图11-25 一端张拉、两端张拉及超张拉时曲线预应力筋中的应力分布(www.xing528.com)

a）一端张拉 b）两端张拉 c）超张拉（A—张拉端；B—固定端）

当预应力筋和承受拉力的设备之间的温差为Δt，预应力筋的线膨胀系数α=0.00001℃^-1，则预应力筋与承受拉力设备之间的温差引起的预应力损失为

σ_l3=αE_sΔt=0.00001×2.0×10⁵×Δt

σ_l3=2Δt （N/mm²） （11-20）

如果采用钢模制作构件，并将钢模与构件一同整体置入蒸汽室（或池）养护，则不存在温差引起的预应力损失。

为了减少温差引起的预应力损失σ_l3，可采用二次升温加热的养护方法，即在略高于常温下养护，待混凝土强度达到7.5～10N/mm²，预应力筋与混凝土粘结在一起时，再二次升温至规定的养护温度。由于混凝土未结硬前温度升高不多，预应力筋受热伸长很小，故预应力损失较小，而混凝土初凝后的再次升温，此时因预应力筋与混凝土两者的膨胀系数相近，故即使温度较高也不会引起预应力损失。

4.预应力钢筋应力松弛引起的预应力损失σ_l4

钢筋在高应力作用下，变形具有随时间而增长的特性。当钢筋长度保持不变（由于先张法台座或后张法构件长度不变）时，则应力会随时间增长而降低，这种现象称为钢筋的松弛（或徐舒）。钢筋的应力松弛使预应力值降低，造成的预应力损失称为σ_l4。

试验表明，松弛的损失与下列因素有关：

（1）时间 早期发展较快，随时间增长，逐渐变慢，最后趋于稳定。大体上在1h内可发展到全部松弛损失的40%～50%；24h内发展到70%～80%；1000h后基本稳定。

（2）钢筋种类 松弛损失随下列钢筋种类依次减小：碳素钢丝及钢绞线、冷轧带肋钢筋、冷拉钢筋及热处理钢筋，即极限强度越高，松弛损失越大；

（3）初始应力 张拉控制应力σ_con越高，松弛损失就越大，损失的速度也越快。如采用消除应力钢丝和钢绞线作预应力筋，当σ_con/f_ptk≤0.5时，实际的松弛损失已很小，可近似取σ_l4=0；当0.5<σ_con/fptk≤0.7时，松弛值与初应力成线性正比关系；当σ_con/f_ptk>0.7时，松弛值与初应力呈非线性关系，松弛值增大较快；

（4）温度 温度越高，松弛损失越大；

（5）张拉方式 采用较高的控制应力1.05σ_con张拉钢筋，持荷2～5min，卸荷到零，再张拉钢筋，使其应力达到σ_con的超张拉程序可比一次张拉（0→σ_con）的松弛损失减小2%～10%σ_con。

预应力钢筋的应力松弛损失σ_l4可按下列公式计算：

1）消除应力钢丝、钢绞线

①普通松弛：

②低松弛：

当σ_con≤0.7f_ptk时

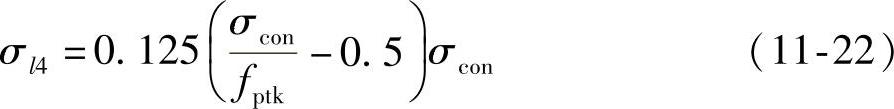
当0.7f_ptk<σ_con≤0.8f_ptk时

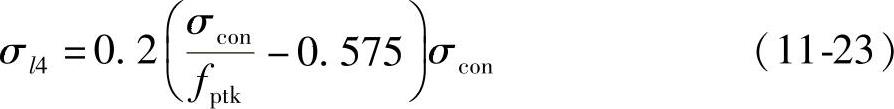
2）中强度预应力钢丝

σ_l4=0.08σ_con （11-24）

3）预应力螺纹钢筋σ_l4=0.03σ_con （11-25）

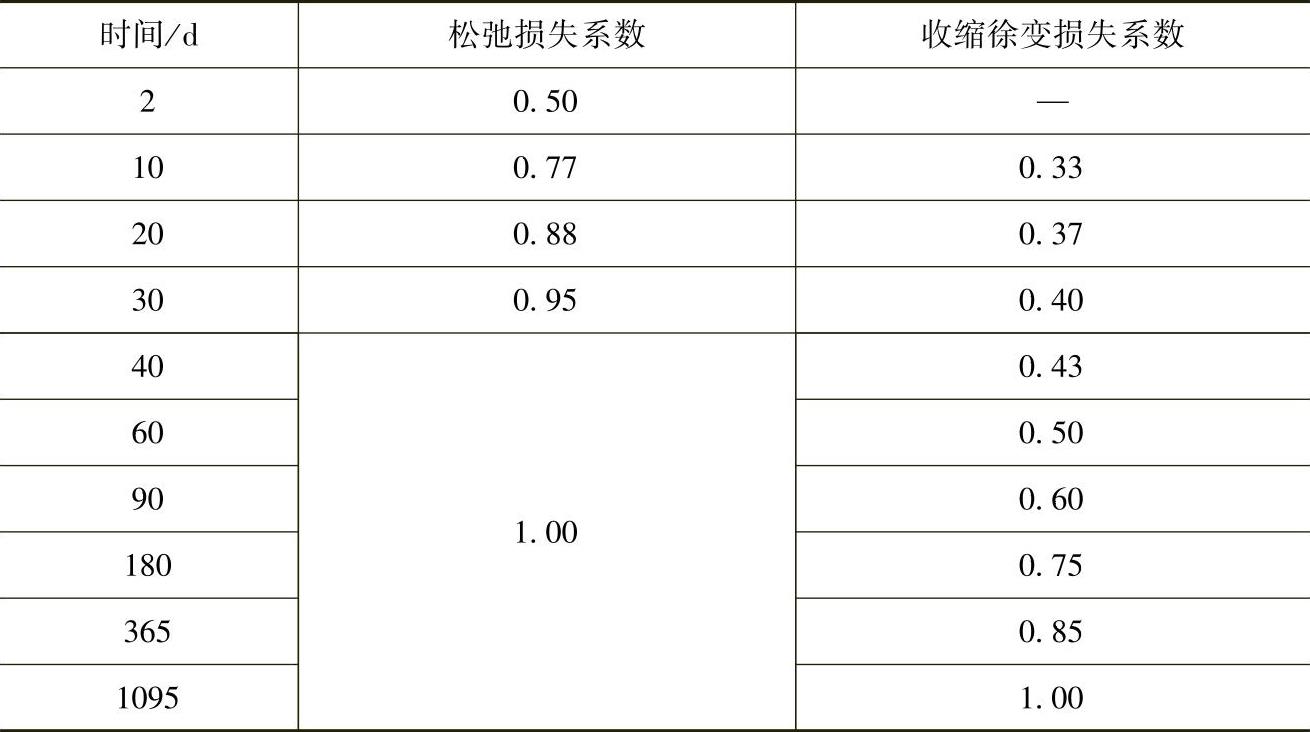
考虑时间影响的预应力钢筋的应力松弛引起的预应力损失值，可由式（11-21）～式（11-25）计算的预应力损失值σ_l4乘以表11-3相应的系数确定。

表11-3 随时间变化的预应力损失系数

减少松弛损失的措施有：超张拉；采用低松弛损失的钢材。低松弛损失指常温20℃条件下，拉应力为70%抗拉极限强度，经1000h后测得的松弛损失不超过2.5%σ_con。

5.混凝土收缩和徐变引起的预应力损失σ_l5

预应力构件由于在混凝土收缩（混凝土结硬过程中体积随时间增加而减小）和徐变（在预应力筋回弹压力的持久作用下，混凝土压应变随时间增加而增加）的综合影响下长度缩短，使预应力筋也随之回缩，从而引起预应力损失。混凝土的收缩和徐变引起预应力损失的现象是类似的，为简化计算，将此两项预应力损失合并考虑为σ_l5。

混凝土收缩和徐变引起受拉区和受压区纵向预应力筋的预应力损失σ_l5、σl′₅可按下列公式计算：

1）先张法构件

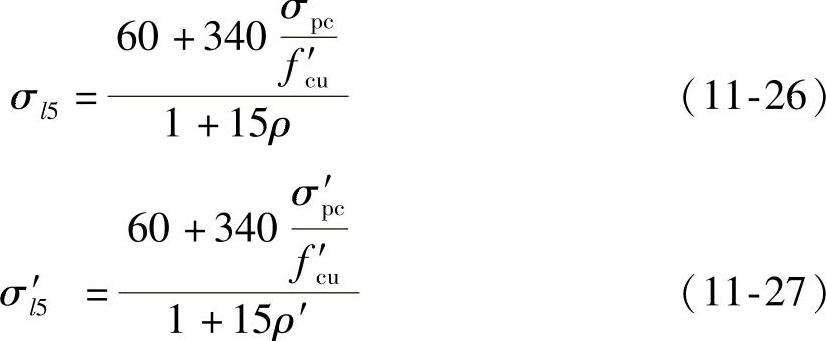
2）后张法构件

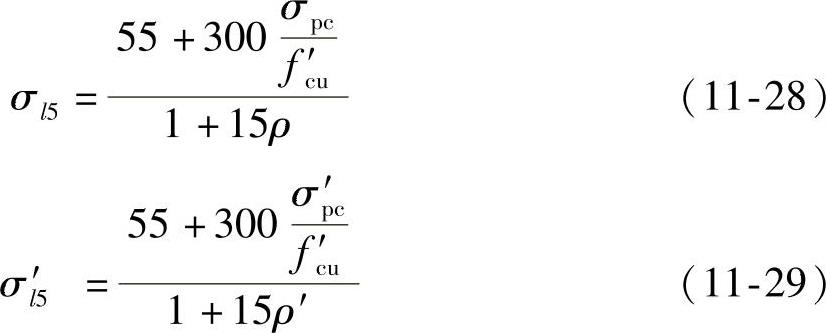
式中 σ_pc、σ′_pc——在受拉区、受压区预应力筋合力点处的混凝土法向压应力；

f_c′_u——施加预应力时的混凝土立方体抗压强度；

ρ、ρ′——受拉区、受压区预应力筋和非预应力筋的配筋率；对先张法构件，ρ=（A_p+A_s）/A₀，ρ′=（A′_p+A′_s）/A₀；对后张法构件，ρ=（A_p+A_s）/A_n，ρ′=（A′_p+A′_s）/A_n；对于对称配置预应力筋和普通钢筋的构件，配筋率ρ、ρ′应按钢筋总截面面积的一半计算。

对于水工预应力混凝土结构，如有论证，混凝土收缩和徐变引起的预应力损失可按其他公式计算。

混凝土法向压应力σ_pc、σ′_pc可按本章11.4节和11.6节的公式求得（即详见轴心受拉构件、受弯构件相应的计算公式），此时，预应力损失值仅考虑混凝土预压前（先张法）或卸去千斤顶时（后张法）的第一批损失，普通钢筋中的应力σ_l5及σ′_l5应取为零。

为了不使得构件混凝土产生非线性徐变，σ_pc、σ′_pc值不得大于0.5f′_cu。

当σ′_pc为拉应力时，式（11-27）及式（11-29）中的σ′_pc应取为零。

计算σ_pc、σ′_pc时，可根据构件制作情况，考虑自重的影响。

从式（11-26）～式（11-29）可以看出，后张法构件的σ_l5与σ′_l5数值比先张法构件要小，这是由于后张法构件在张拉预应力筋前混凝土的部分收缩已经完成，因此对应力损失的影响相应地减少了。

式（11-26）～式（11-29）仅适合于相对湿度为60%～80%环境下的结构构件。当结构处于年平均相对湿度低于40%的环境下，σ_l5及σ′_l5值应增加30%。对处于高湿度环境下的结构（如水池、水管、桩等），σ_l5及σ′_l5值应减少50%。当采用泵送混凝土时，宜根据实际情况考虑混凝土收缩、徐变引起的预应力损失值的增大。对重要的结构构件，当需要考虑与时间相关的混凝土收缩、徐变及钢筋应力松弛引起的预应力筋的预应力损失终极值时，可按下列公式计算：

1）受拉区纵向预应力筋应力损失终极值σ_l5

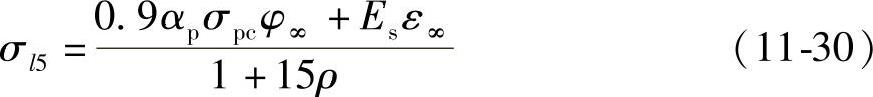
式中 σ_pc——受拉区预应力筋合力点处由预加力（扣除相应阶段预应力损失）和梁自重产生的混凝土法向压应力，其值不得大于0.5f′_cu；对简支梁可取跨中截面与四分之一跨度处截面的平均值；对连续梁和框架可取若干有代表性截面的平均值；

φ_∞——混凝土徐变系数终极值；

ε_∞——混凝土收缩应变终极值；

E_s——预应力筋的弹性模量；

α_p——预应力筋弹性模量与混凝土弹性模量的比值；

当无可靠资料时，ε_∞、φ_∞值可按表11-4及表11-5采用。如结构处于年平均相对湿度低于40%的环境下，表列数值应增加30%。

表11-4 混凝土收缩应变终极值ε_∞（×10^-4）

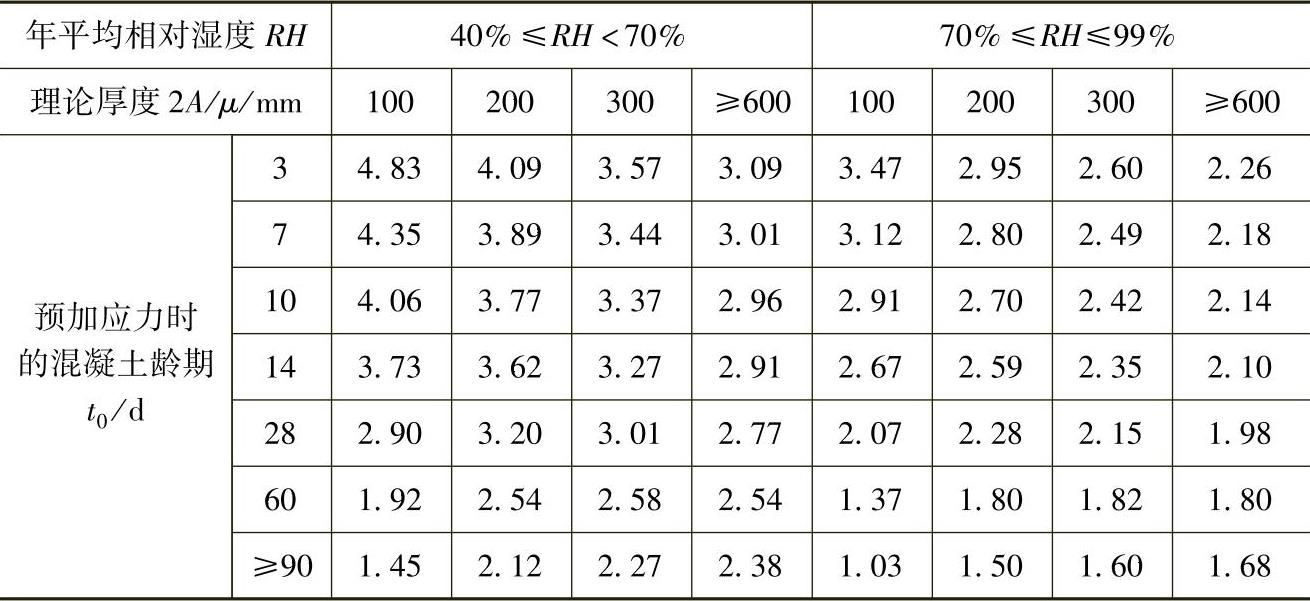
表11-5 混凝土徐变系数终极值φ_∞

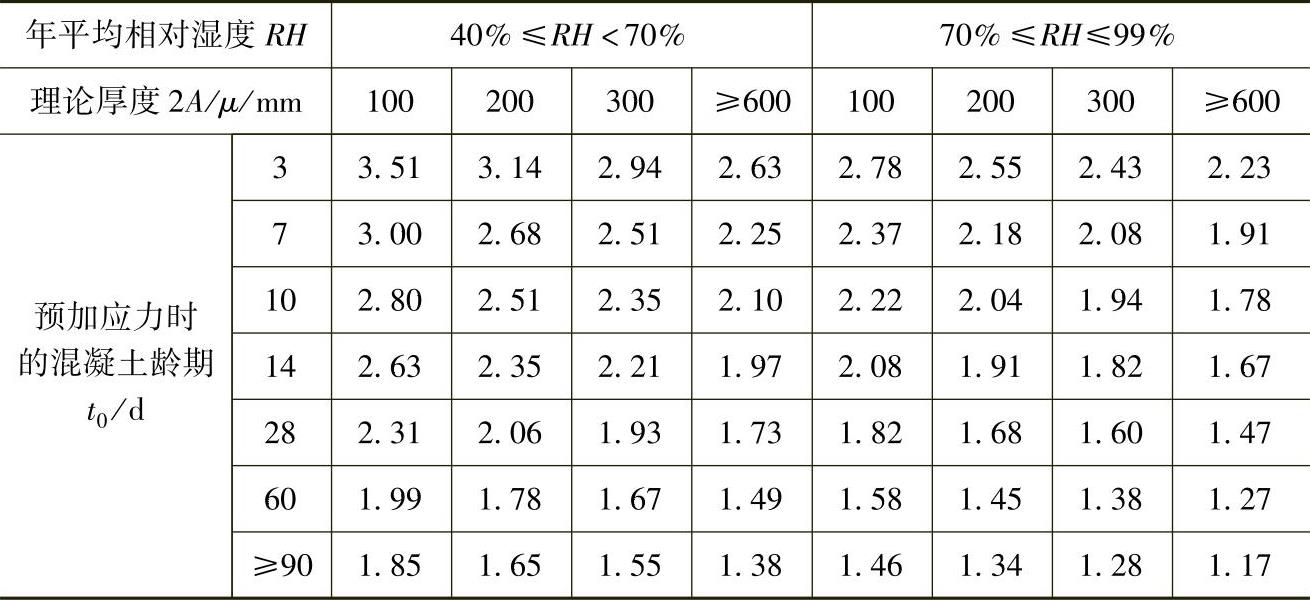
注：1.预加力时的混凝土龄期，先张法构件可取3～7d，后张法构件可取7～28d；

2.A为构件截面面积，u为该截面与大气接触的周边长度；当构件为变截面时，A和u均可取其平均值；

3.本表适用于由一般的硅酸盐类水泥或快硬水泥配置而成的混凝土；表中数值系按强度等级C40混凝土计算所得，对C50及以上混凝土，表列数值应乘以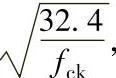式中f_ck为混凝土轴心抗压强度标准值（MPa）；

4.本表适用于季节性变化的平均温度-20℃～+40℃；

5.当实际构件的理论厚度和预加力时的混凝土龄期为表列数值的中间值时，可按线性内插法确定。

2）受压区纵向预应力筋应力损失终极值σ′l5

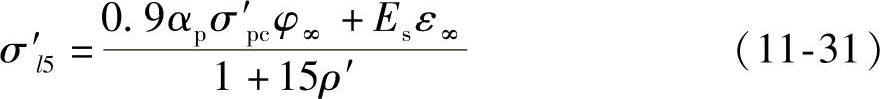
式中 σ′_pc——受压区预应力筋合力点处由预加力（扣除相应阶段预应力损失）和梁自重产生的混凝土法向压应力，其值不得大于0.5f′_cu，当σ′_pc为拉应力时，取σ′_pc=0。

对受压区配置预应力筋A′_p及普通钢筋A′_s的构件，在计算式（11-30）、式（11-31）中的σ_pc及σ′_pc时，应按截面全部预加力进行计算。

考虑时间影响的混凝土收缩和徐变引起的预应力损失值，可由式（11-30）和式（11-31）计算的预应力筋应力损失终极值σ_l5、σ′_l5乘以表11-4及表11-5中相应的系数确定。

混凝土徐变变形与混凝土受到的预压应力σ_pc有关，σ_pc越大则徐变也越大；徐变变形还与预压时的混凝土立方体强度f′_cu有关，f′_cu越大则徐变越小。当σ′_pc/f′_cu≤0.5时，混凝土仅产生线性徐变，预应力损失可近似地按线性变化考虑；当σ_pc/f′_cu大于0.5时，混凝土将产生非线性徐变，预应力损失会迅速增加。所以在设计中，对σ_pc应加以适当限制。实测表明，混凝土收缩和徐变引起的预应力损失σ_l5很大，约占全部预应力损失的40%～50%，所以应当采取各种有效措施减少混凝土收缩和徐变。

为了减少此项损失，可采用高强度等级的水泥，减少水泥用量，降低水灰比，振捣密实，加强养护，并应控制混凝土的预压应力σ_pc、σ′_pc值不超过0.5f′_cu。

6.螺旋式预应力钢丝（或钢筋）挤压混凝土引起的预应力损失σl6

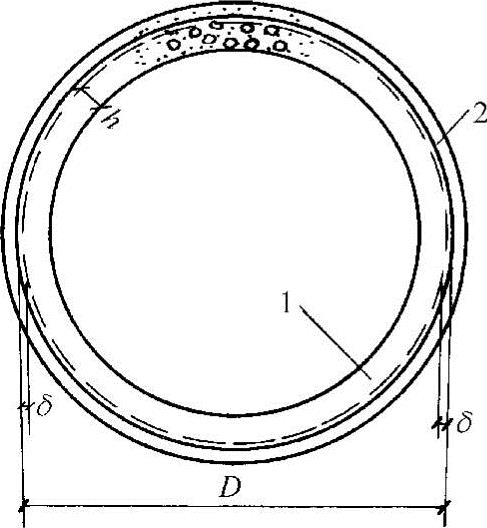
图11-26 环形配筋的预应力构件

1—环形截面构件 2—预应力筋

D、h、δ—直径、壁厚、压陷变形

环形结构构件（如水管、油罐等）的混凝土被螺旋式预应力筋箍紧，使混凝土产生环向压力，以抵抗内压。混凝土受环向预应力筋的挤压会发生局部压陷，构件直径将减少2δ，使得预应力筋回缩，从而引起预应力损失σ_l6，见图11-26。σ_l6的大小与构件直径有关，构件直径越小，压陷变形的影响越大，预应力损失也就越大。当结构直径大于3m时，损失就可不计；当结构直径小于或等于3m时，σ_l6可取为

σ_l6=30N/mm² （11-32）

后张法构件的预应力筋采用分批张拉时，应考虑后批张拉预应力筋所产生的混凝土弹性压缩（或伸长）对先批张拉预应力筋的影响，将先批张拉预应力筋的张拉控制应力值σ_con增加（或减小）α_Eσ_pci。此处，σ_pci为后批张拉预应力筋在先批张拉预应力筋重心处产生的混凝土法向应力，α_E为预应力预应力筋弹性模量与混凝土弹性模量的比值。

上述各项预应力损失并不同时发生，而是按不同张拉方式分阶段发生的。通常把在混凝土预压前出现的损失称为第一批预应力损失σ_lⅠ（先张法指放张前，后张法指卸去千斤顶前的损失），混凝土预压后出现的损失称为第二批预应力损失σ_lⅡ。总的损失σ_l=σ_lⅠ+σ_lⅡ。各批的预应力损失组合见表11-6。

表11-6 各阶段预应力损失值的组合

注：1.先张法构件第一批损失值计入σ_l2是指有折线式配筋的情况；

2.先张法构件，σ_l4在第一批和第二批损失中所占的比例，如需区分，可按实际情况确定。

对预应力构件除应按使用条件进行承载力及抗裂、裂缝宽度、变形验算以外，还需对构件在制作、运输、吊装等施工阶段进行承载力验算，对施工阶段预拉区不允许出现裂缝的构件或预拉区允许出现裂缝而在预拉区不配置纵向预应力筋的构件或预压时全截面受压的构件尚应进行截面边缘混凝土法向应力的验算。不同的受力阶段（即根据构件的实际情况）应考虑相应的预应力损失值的组合。

考虑到预应力损失的计算值与实际值可能有误差，为确保构件安全，按上述各项损失计算得出的总损失值σ_l小于下列数值时，应按下列数值采用：

先张法构件 100N/mm²

后张法构件 80N/mm²