10.7.5双向板支承梁设计与钢筋混凝土结构

支承梁的实际荷载分布较为复杂。实用设计法中，双向板沿两个方向传给支承梁的荷载是按图10-55近似确定：从板的四角作45°线与平行于长边的中线相交，将板划分为四个部分。每块小板面积内的荷载传给与其相邻的支承梁上。此时短跨支承梁承受三角形荷载，长跨支承梁承受梯形荷载。计算支承梁时，仍应考虑活荷载在梁各跨的最不利布置。

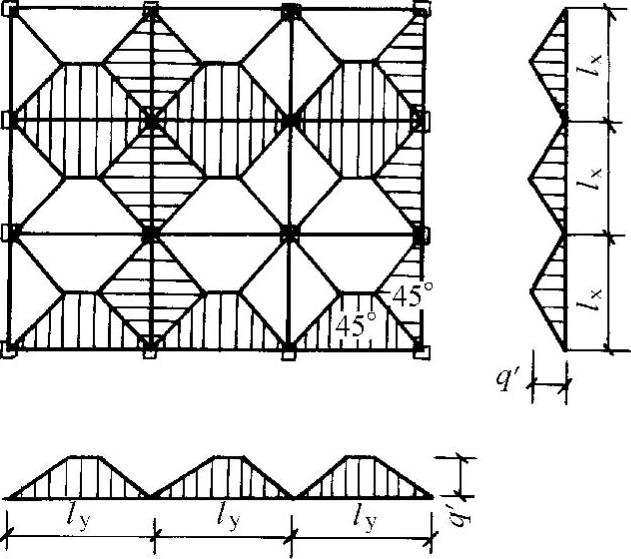
图10-55 双向板支承梁的荷载分配

为计算方便，一般将梁上的三角形、梯形荷载按照支座固端弯矩等效的原则换算成等效均布荷载q_e（图10-56）：

三角形荷载

图 10-56

梯形荷载 q_e=（1-2α²+α³）q′ （10-38）

支承梁的内力可按弹性理论或塑性理论计算。按弹性理论计算时，对于等跨或跨度相差不超过10%的连续梁，可利用附表17，以等效均布荷载q_e计算其支座弯矩，再求出各跨在三角形或梯形荷载下的简支梁弯矩，将简支梁弯矩与支座负弯矩连线图迭加即可求得跨内最大正弯矩。

按塑性理论计算时，可先在按弹性理论计算的支座弯矩基础上，应用调幅法确定支座弯矩，再按实际荷载求出简支梁弯矩，进而求出跨内最大正弯矩。

双向板支承梁的截面配筋计算及构造要求与单向板肋梁楼盖的支承梁相同。

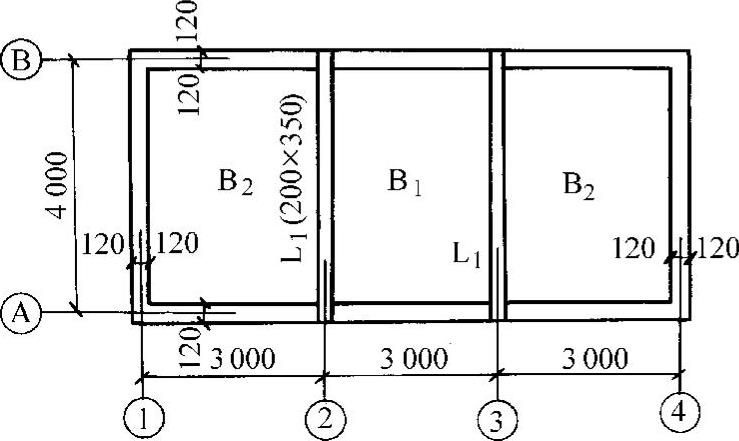
图 10-57

【例10-2】 某双向板肋梁楼盖，平面布置如图10-57所示，活荷载3kN/m²，梁截面尺寸bh=200mm×350mm，板面用20mm厚水泥砂浆抹面，板底用15mm厚石灰砂浆粉刷，混凝土采用C25，钢筋采用HPB300级，试设计此双向板楼盖。

【解】 1.按弹性理论计算双向板的配筋

（1）确定板厚：h=80mm>l_x/50=3000/50mm=60mm

（2）荷载计算：

20mm水泥砂浆抹面 20kN/m³×0.02=0.40kN/m²

板自重 25kN/m³×0.08=2kN/m²

15mm石灰砂浆粉刷 17kN/m³×0.015=0.26kN/m²

恒载标准值 g_k=2.66kN/m²

活载标准值 q_k=3.00kN/m²

恒载设计值 g=1.2×2.66kN/m²=3.192kN/m² 1.35×2.66=3.591

活载设计值 q=1.4×3kN/m²=4.2kN/m² 1.4×0.7×3=2.94

总荷载设计值 p=（3.192+4.2）kN/m²=7.392kN/m²

（3.591+2.94）kN/m²=6.531kN/m²

由计算结果可见，由可变荷载效应控制的组合控制设计荷载。

（3）计算跨度

B₁，l_x=3m，l_y=（4.0-0.24+0.08）m=3.84m

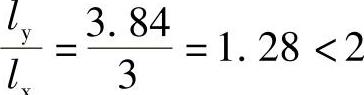，为双向板

B₂，l_x=（3-0.12+0.04）m=2.92m，l_y=3.84m

，为双向板

（4）内力计算

计算跨中弯矩时，荷载取值为：

p′=g+q/2=（3.192+2.1）kN/m²=5.292kN/m²

p″=q/2=2.1kN/m²

计算支座弯矩时，荷载取值为

p=7.392kN/m²

荷载布置及计算简图如图10-58所示。

B₁，l_x/l_y=3/3.84=0.78，由附表18查弯矩系数。

跨中弯矩 M_x=（0.03732×5.292+0.06394×2.1）×3²kN·m/m=（1.78+1.208）kN·m/m=2.99kN·m/m

M_y=（0.01568×5.292+0.04248×2.1）×3²kN·m/m=（0.7468+0.8029）kN·m/m=1.55kN·m/m

支座弯矩 M_a1=-0.079×7.392×3²=-5.256kN·m(www.xing528.com)

B₂，l_x/l_y=2.92/3.84=0.76

跨中弯矩 M_x=（0.0519×5.292+0.06618×2.1）×2.92²kN·m/m=（2.342+1.185）kN·m/m=3.527kN·m/m

M_y=（0.02596×5.292+0.04216×2.1）×2.92²=（1.171+0.755）kN·m/m=1.926kN·m/m

支座弯矩 M_a2=-0.104×7.392×2.92²kN·m/m=-6.555kN·m

支座a的弯矩应取相邻两区格计算的平均值，即

M_a=-（5.256+6.555）/2kN·m/m=-5.906kN·m/m

（5）配筋计算：A_s=M/（γ_sh₀f_y），取γ_s=0.95

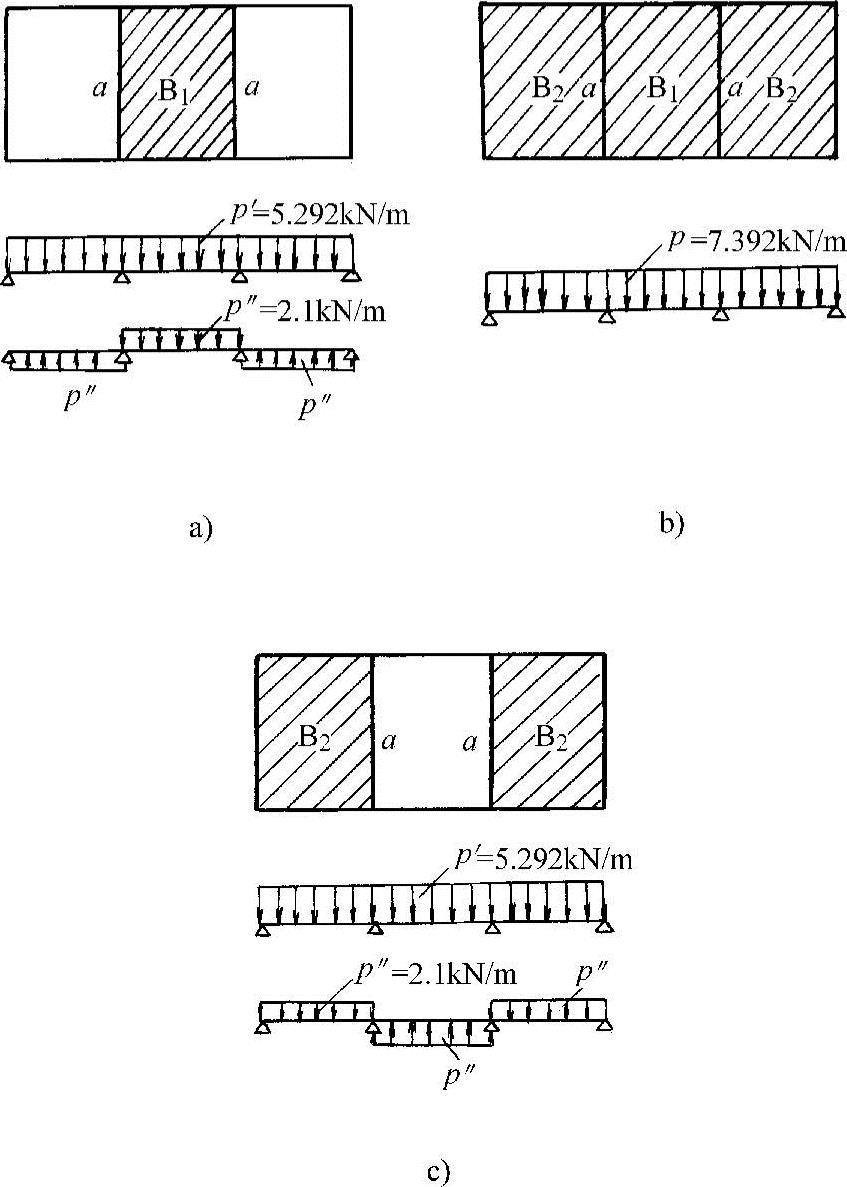
图 10-58

a）B₁求跨中M时的计算简图 b）求支座M时的计算简图

c）B₂求跨中M时的计算简图

短跨 h₀=（80-20）mm=60mm 长跨 h₀=（80-30）mm=50mm

钢筋设计强度f_y=270N/mm²，计算结果见表10-10，配筋图见图10-59。

2.按塑性理论计算双向板的配筋

h=80mm，h_0x=60mm，h_0y=50mm

B₁，l_x=（3.0-0.2）m=2.8m

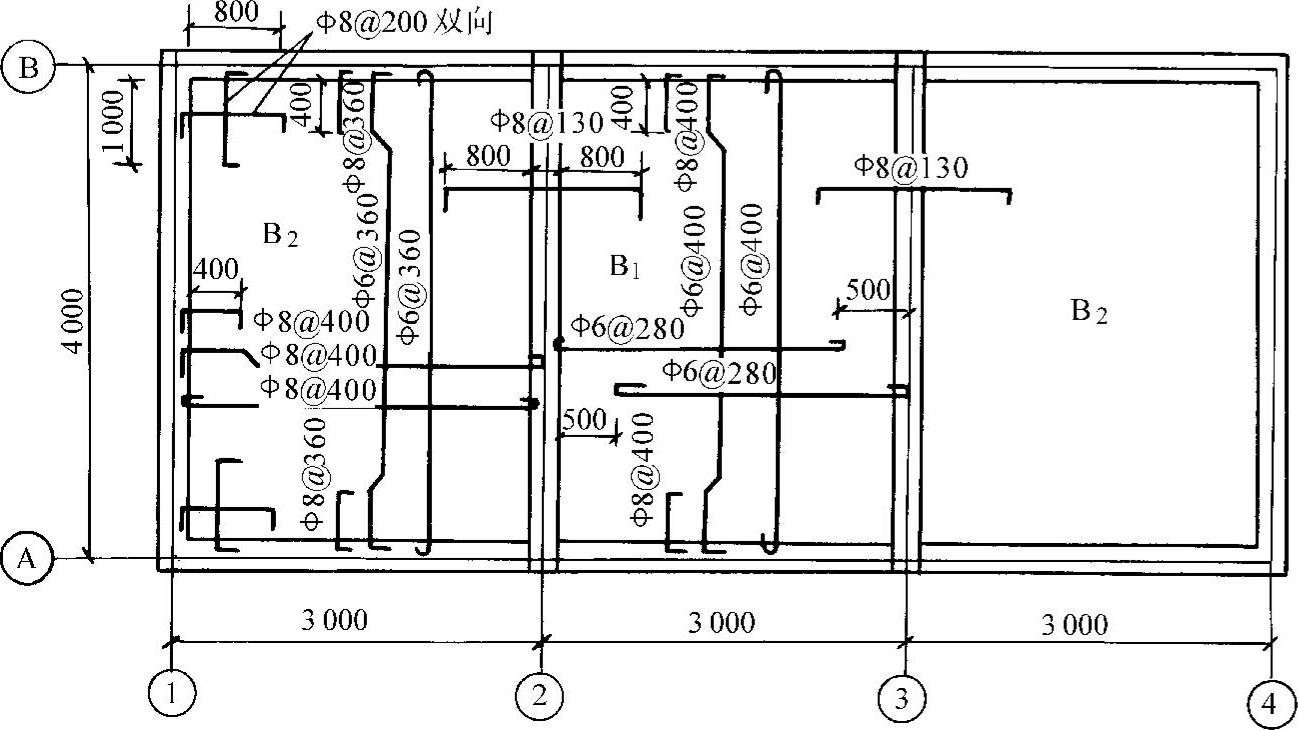
图 10-59

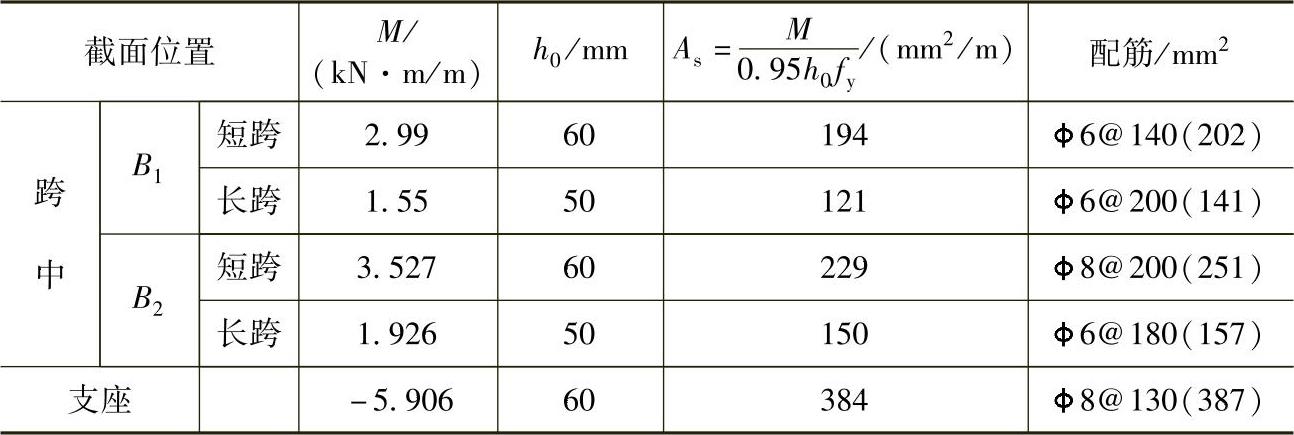
表10-10 双向板配筋计算

注：支座负M可取支座边缘处的弯矩值，这里为了简化，取支座中线处的弯矩值。

l_y=（4.0-0.24+0.08）m=3.84m

n=l_y/l_x=3.84/2.8=1.37

取 α=0.55，β=2.0

长跨支座弯矩 m′_y=m″_y=0

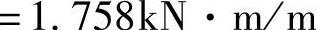
m_y=αm_x=0.55×1.758kN·m/m=0.967kN·m/m

m′_x=m″_x=2m_x=2×1.758kN·m/m=3.516kN·m/m

B₂，l_x=（3.0-0.1-0.12+0.04）m=2.82m

l_y=3.84m

n=l_y/l_x=3.84/2.82=1.36，取α=0.55

已知短跨支座弯矩m′_x=3.516kN·m/m

而 M′_x=l_ym′_x=nl_xm′x

m_y=0.55×3.385kN·m/m=1.862kN·m/m

配筋计算：A_s=M/（γ_sh₀f_y）

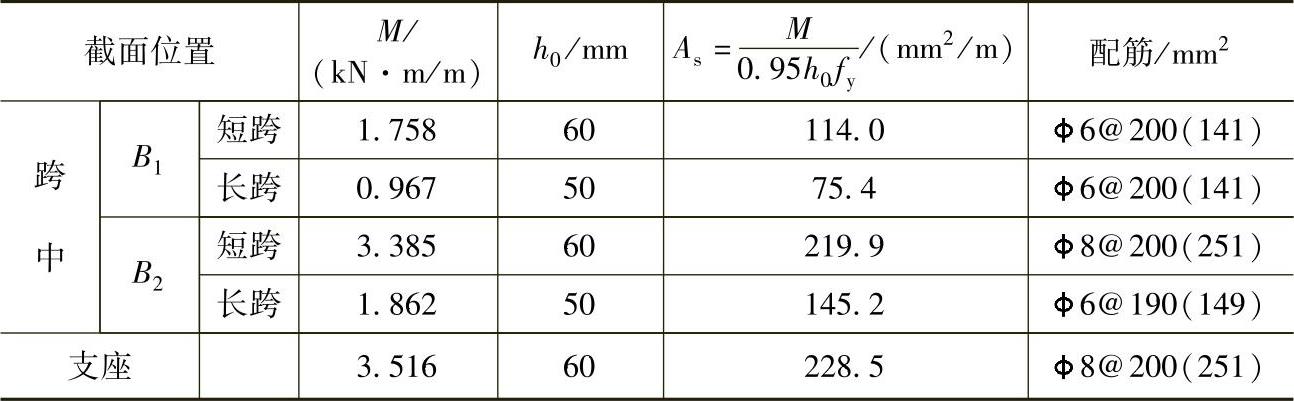
近似取γ_s=0.95，计算结果见表10-11，配筋图见图10-60。

图 10-60

表10-11 双向板配筋计算