用塑性理论计算10.7.3双向板的钢筋混凝土结构

双向板按考虑塑性内力重分布的方法计算，既能较好地符合板的实际受力情况，又能节约材料，与按弹性理论计算相比，一般可节约钢筋20%～30%。同时计算亦较为方便。

目前常用的塑性理论计算方法有塑性铰线法、板带法以及用电子计算机分析的最佳配筋法等，其中塑性铰线法应用较多。

1.塑性铰线法的基本原理

塑性铰线法的主要依据和基本假设如下：

（1）塑性铰线由钢筋屈服而产生，沿塑性铰线单位长度上的弯矩为常数，等于板的极限弯矩。

（2）在均布荷载作用下，塑性铰线为直线。塑性铰线将板分割成若干板块，形成可变体系。

（3）板块内的弹性变形远小于塑性铰线处的变形，可忽略不计，所以可将各板块视作平面刚体，整个板块变形都集中在塑性铰线处。破坏时各板块都绕塑性铰线转动。

（4）塑性铰线上的剪力、扭矩很小，可认为等于零。

塑性铰线一般形成在最大弯矩截面上。此外，其位置还和板的平面形状、边界条件、荷载形式、配筋方式及数量等因素有关。

如图10-47所示，沿负弯矩最大的固定边界，一般出现负塑性铰线；短跨跨中最大正弯矩处一般可作为正塑性铰线的起点，而且正塑性铰线应该通过相邻板块转动轴的交点，而支承边正是转动轴线。当板支承于柱上时，其转动轴将通过柱顶。

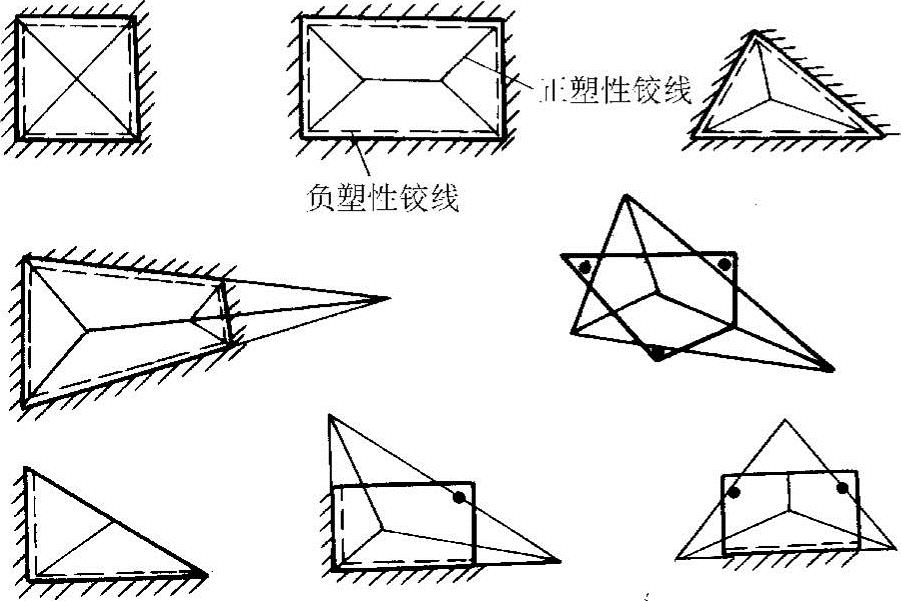
图10-47 板块的塑性铰线

塑性铰线法有两种计算途径：能量法和板块极限平衡法。能量法是依据破坏机构产生微小虚运动时，外荷载所做的外功和内力所做的内功相等的原理建立的，所以又称虚功法或机动法。板块极限平衡法是通过考虑被塑性铰线所分割的各板块的平衡条件而建立起来的。下面仅介绍板块极限平衡法。

2.板块极限平衡法

（1）平衡方程的建立 板块极限平衡法的前提是确定导致板形成可变体系而破坏的塑性铰线位置。图10-48a所示为多区格矩形双向板的任一中间区格板及其塑性铰线。假设角部塑性铰线与板边的夹角为45°，一般双向配筋面积比在一定范围内时，这一假设是合理的。

设板面作用均布极限荷载p=g+q。

设跨内正塑性铰线沿l_x和l_y方向的总极限弯矩分别为M_x和M_y；支座负塑性铰线沿l_x和l_y方向的总极限弯矩分别为M′_x、M″_x和M′_y、M″_y。

由塑性铰线分割而成的四个板块，每个板块都应满足各自的内外力平衡条件。

板块ABFE（图10-48b），由ΣM_AB=0得

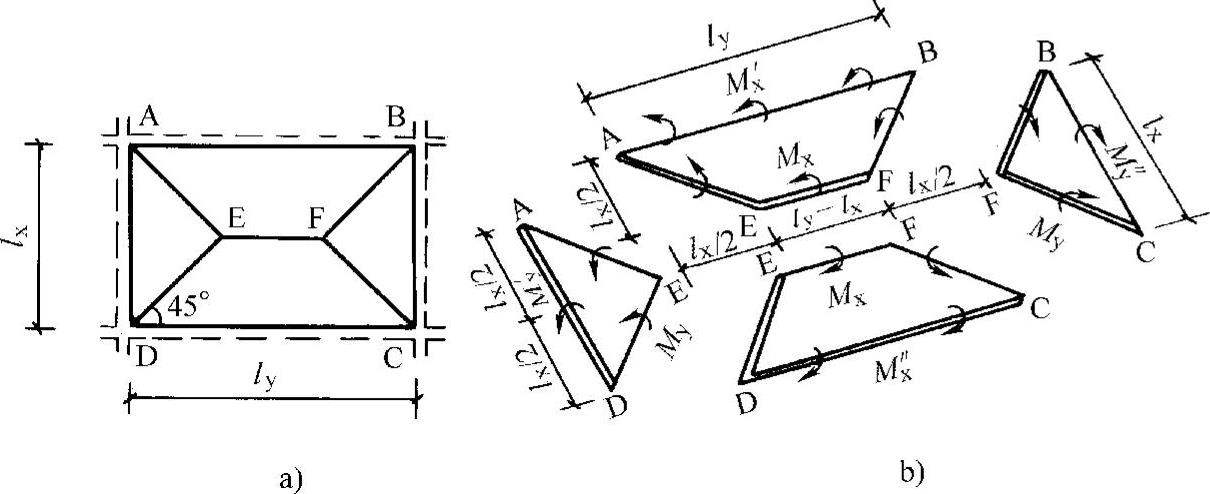
图10-48 双向板的极限平衡

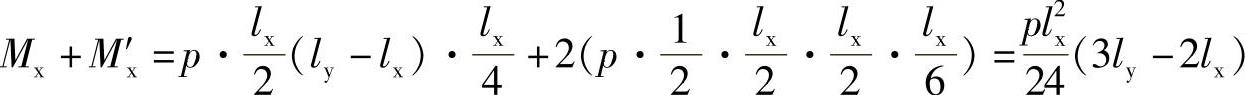
板块CDEF，由ΣM_CD=0得

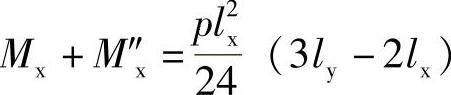
板块AED（图10-48b），由ΣM_AD=0得

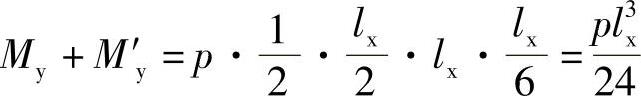
板块CFB，由ΣM_BC=0得

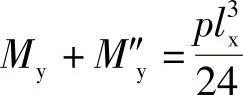
将以上四式相加，即可得到四边固定双向板塑性铰线上总极限弯矩所应满足的平衡方程式：

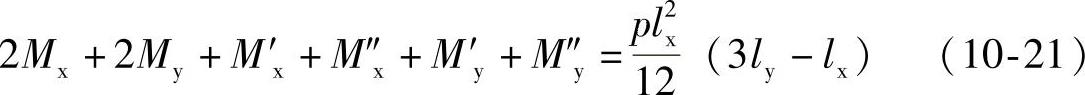
四边简支板支座弯矩M′_x=M″_x=M′_y=M″_y=0，则平衡方程为：

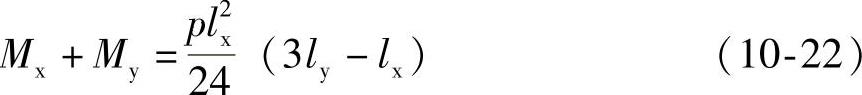
（2）双向板的极限弯矩 如令m代表板单位宽度的极限弯矩（m可由配筋量计算，m=A_sf_yγ_sh₀，γ_sh₀为受拉钢筋的力臂；γ_s为力臂系数；h₀为截面有效高度；A_s为单位板宽上的纵向受拉钢筋截面积）。并设(www.xing528.com)

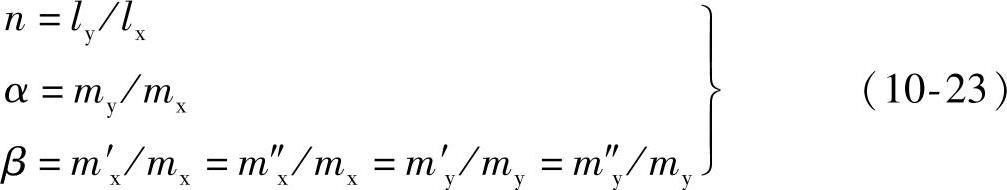
则有

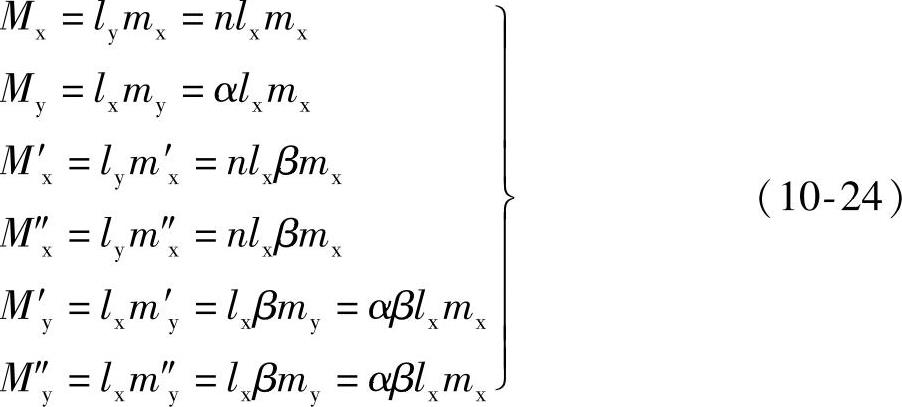
将关系式（10-24）代入式（10-21）得

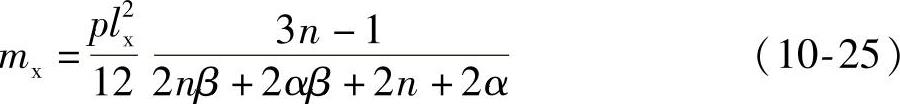
或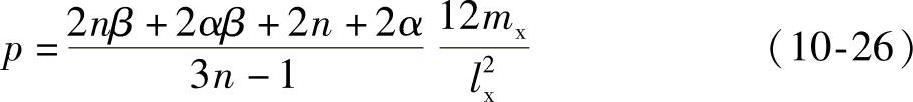

对于四边简支板，则为

或

式中 p——双向板的极限均布荷载；

m_x——短跨跨中单位板宽上的极限弯矩。

（3）双向板按塑性理论计算的设计公式 设计双向板时，通常已知板的设计荷载p=g+q和净跨l_x及l_y，要求确定内力和配筋。在四边连续板的一般情况下，有四个内力未知量：m_x，m_y，m′_x=m″_x，m′_y=m″_y，而只有一个方程式，不能求解，故需预先选定内力间的比值α=m_y/m_x及β=m′_x/m_x=m″_x/m_x=m′_y/m_y=m″_y/m_y值。考虑到与弹性弯矩比值不要相差太多，并便于板的配筋构造和节省钢筋，根据经验，设计时可取α≈1/n²，β=1.5～2.5（对于中间区格取β=2～2.5）。

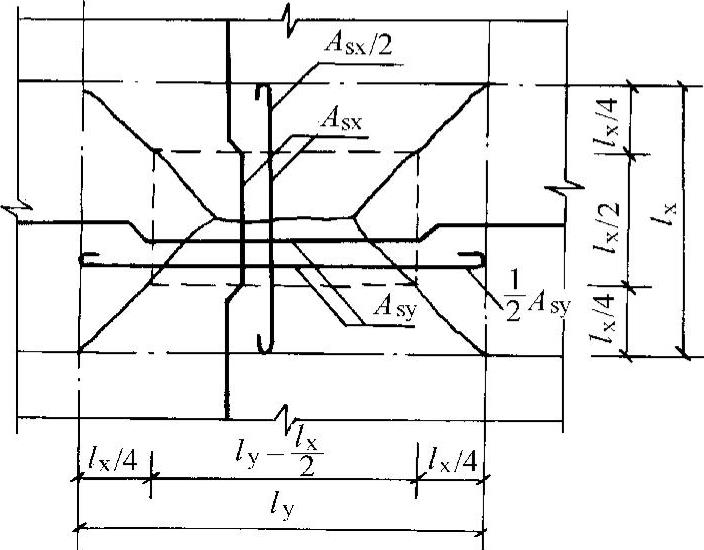
图10-49 跨中钢筋弯起

为了充分利用钢筋，可将连续板的跨中正弯矩钢筋，在距支座一定距离处截断或弯起一部分（弯起的钢筋可作为支座抵抗负弯矩钢筋的一部分），如图10-49所示。但是，为保证安全，不宜将正弯矩钢筋过早截断或弯起，其数量也不宜过多。通常两个方向均在距支座l_x/4处将一半钢筋截断或弯起，这样，在靠支座l_x/4以内的跨中塑性铰线上的单位板宽的极限弯矩为m_x/2（或m_y/2），故此时两个方向的跨中总的弯矩分别为

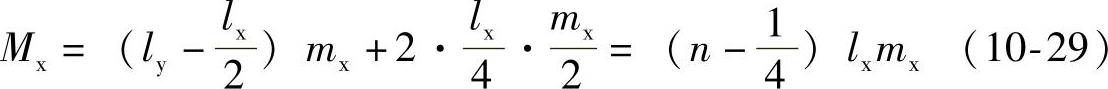
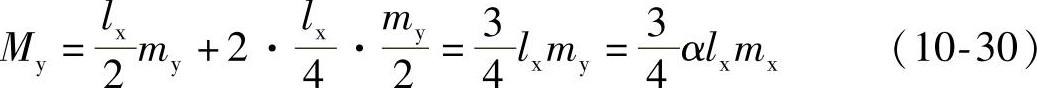
支座弯矩M′_x、M″_x、M′_y及M″_y仍按式（10-24）计算。

按上述关系将各弯矩代入式（10-21）中，可得

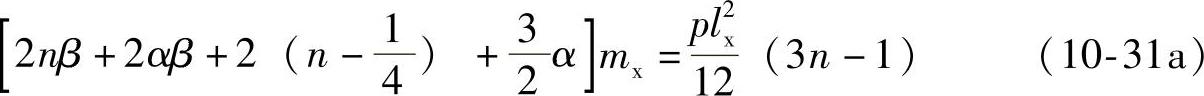
或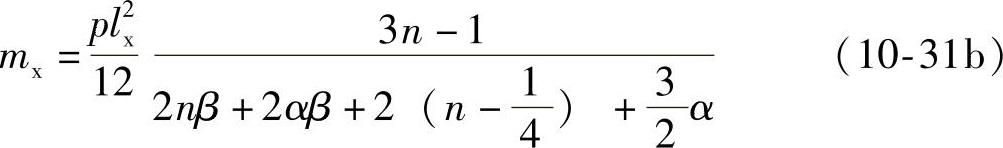

式中2nβ项与短跨方向支座弯矩M′_x及M″_x对应；2αβ项与长跨方向支座弯矩M′_y及M″_y相对应；2（n-1/4）与短跨跨中弯矩M_x相对应；3α/2与长跨跨中弯矩M_y相对应。式（10-31）代表四边连续双向板在距支座l_x/4处跨中钢筋弯起或截断一半时的一般公式。对于其他支承情况或板的某边支座弯矩为已知时，只需将上式稍加改变仍可应用。例如：

（1）当三边连续，一长边为简支时，只需将式（10-31b）中的2nβ换为nβ即可，其他不变，即

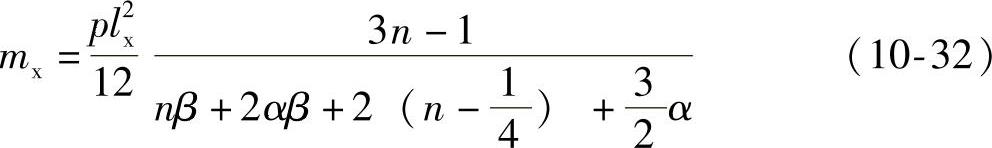
（2）三边连续，一短边为简支时，只需将式（10-31）中的2αβ换为αβ即可，其他不变，即

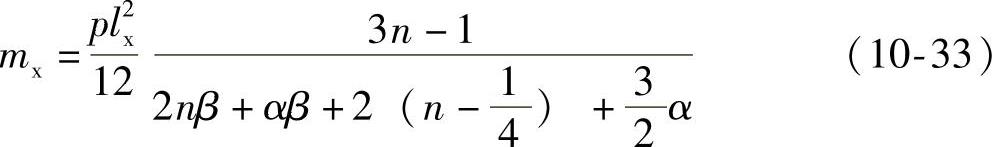
（3）两邻边连续，其余两邻边简支的板，

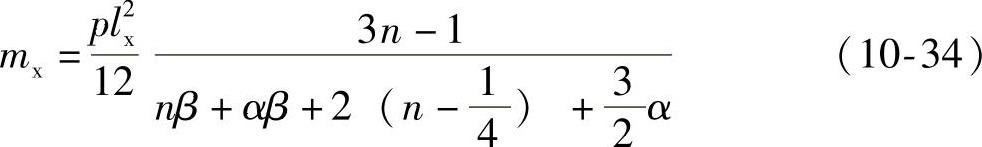
（4）当四边连续板的某一支座钢筋为已知时（通常是该支座已由相邻区格的板计算出支座的配筋），则对所考虑的区格来说，该支座的极限弯矩即为已知，这时可将已知的弯矩值代入式（10-31a）中相应的支座弯矩项，并移至等式右侧与已知的荷载项归并，同样可解出m_x。例如，当板的一个长跨方向支座弯矩M′_y为已知时，即M_y′=l_xm_y′，此处，m_y′为由相邻区格板求得的单位长度支座弯矩值。代入式（10-31a）可得

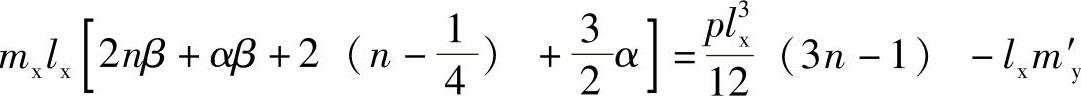
或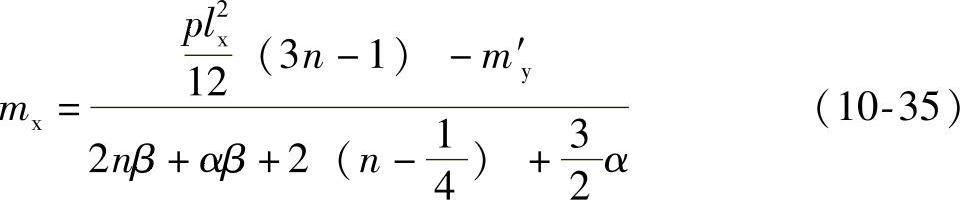

如其他支座弯矩已知，同样可推出相应的计算公式。