受弯构件挠度计算方法

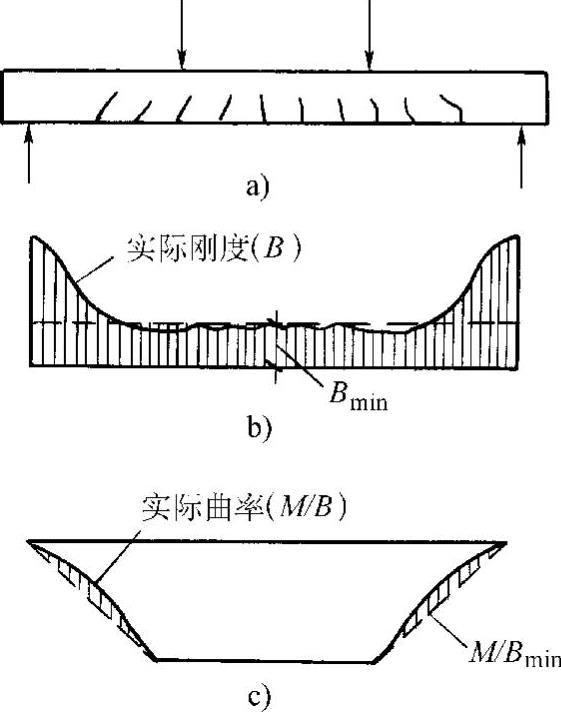
图9-12 构件的实际刚度、曲率变化

在求得截面刚度后，构件的挠度可按结构力学方法进行计算。如上所述，梁的刚度随内力的增大而减小。在荷载作用下，同一根梁各截面内力一般是不相同的，因而各截面的刚度也将不同。如在承受对称集中荷载的简支梁内，除两集中荷载间的纯弯区段外，剪跨区各截面的弯矩是不相等的。越靠近支座，弯矩越小，因而其刚度越大。在支座附近的截面将不出现裂缝，其刚度将较已出现裂缝的区段大很多（图9-12）。由此可见，沿梁长各截面的平均刚度是变值。为了简化计算，在实用上，在同一符号弯矩区段内，截面的刚度均可按该区段的最小刚度计算，亦即按最大弯矩处的截面刚度计算（如图9-12b所示）。也就是平均曲率φ按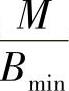计算（图9-12中虚线所示），这是偏于安全的。这一计算原则通常称为最小刚度原则。

采用最小刚度原则计算挠度，虽然会产生一些误差，但在一般情况下误差是不大的，这是因为，一方面，采用最小刚度原则计算，相当于在计算曲率φ时，多算了图9-12c中阴影线表示的面积。从材料力学中已知，支座附近的曲率对简支梁的挠度影响很小，且其计算值偏大，偏于安全。另一方面，按上述方法计算挠度时，只考虑弯曲变形的影响，而未考虑剪切变形的影响。在匀质材料梁中，剪切变形一般很小，可以忽略，但在剪跨区已出现斜裂缝的钢筋混凝土梁中，剪切变形将较大。同时，沿斜截面弯曲也将使剪跨内钢筋应力较按垂直截面受弯增大。也就是说，当未考虑斜截面裂缝出现的影响时，挠度计算值将偏小。由此可见，在一般情况下，使计算值偏大和偏小的因素大致相互抵消，因此，在计算中采用最小刚度原则是可行的。计算结果与试验结果符合较好。

在斜裂缝出现较早、较多，且延伸较长的薄腹梁中，斜裂缝的不利影响较大，按上述方法计算的挠度值可能偏低较多。目前由于试验数据不足，尚不能提出具体的修正方法，计算时应酌情增大。

对于连续梁的挠度计算，最小刚度原则仍然适用，因此，规范规定，在等截面构件中，可假定各同号弯矩区段内的刚度相等，并取该区段内最大弯矩处的刚度，即该区段内最小刚度。

理论分析表明，在计算跨度内的支座截面刚度不大于跨中截面刚度的两倍或不小于跨中截面刚度的二分之一的情况下，若按该跨为等刚度，且构件刚度取跨中最大弯矩截面的刚度，即跨中区段的最小刚度，计算结果与上述各同号弯矩区段内的最大弯矩处的刚度计算结果相比，其误差不会大于5%。因此，该跨也可按等刚度构件进行计算，其构件刚度可取跨中最大弯矩截面的刚度。在弯矩变号时，（即弯矩有正有负时）可分别取同号弯矩区段内|M|_max处的最小刚度来计算挠度。用B_min替代匀质弹性体的截面抗弯刚度E_cI₀以后，梁的挠度计算可按一般的材料力学公式进行。对照式（9-35），钢筋混凝土受弯构件的挠度可按下式计算：

式中 C——与荷载类型与支承条件有关的系数；

M_q——按荷载准永久组合计算的弯矩值；

B——按荷载效应的标准组合并考虑荷载长期作用影响后的刚度，在同号弯矩区段内取最小值。

由式（9-57）计算的挠度应不超过表9-2规定的挠度限值f_lim。(www.xing528.com)

【例9-3】 数据同【例9-1】，若挠度限值为l₀/250，试计算其跨中挠度是否满足要求。

【解】 由【例9-1】已知M_q=58.85kN·m，ψ=0.651，α_E=6.67。

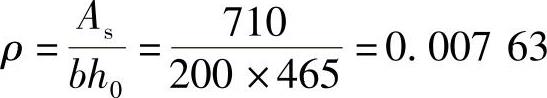
梁的短期刚度为

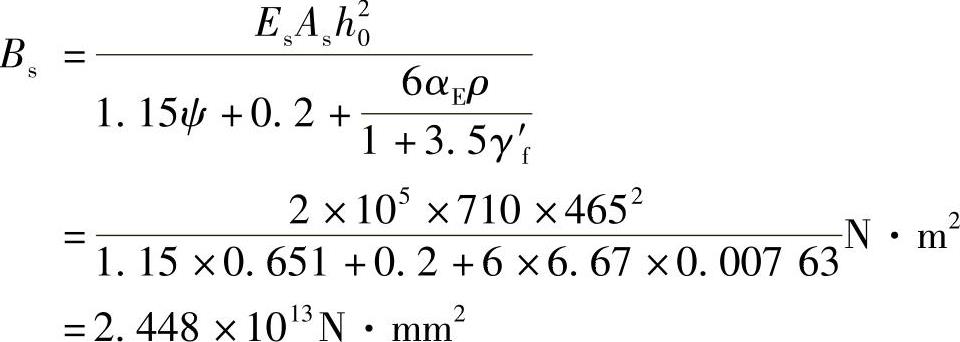
因ρ′=0，所以θ=2.0。梁的长期刚度为

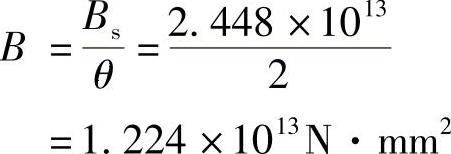
梁的挠度

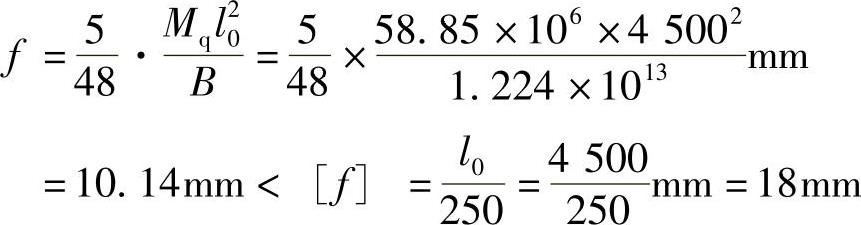
满足要求。