受弯构件短期刚度分析|钢筋混凝土结构

1.平均应变和平均截面裂缝出现以后，梁处于第Ⅱ阶段。即使在纯弯区段内，钢筋混凝土的应变（或应力）分布也是不均匀的（图9-9）。由纯弯区段内钢筋混凝土梁的试验可知，这一阶段的应变分布具有下列特征：

（1）钢筋应变沿梁长呈波浪形变化。在开裂截面，应变最大，裂缝之间应变较小。钢筋的平均应变ε_sm已由前节求得为

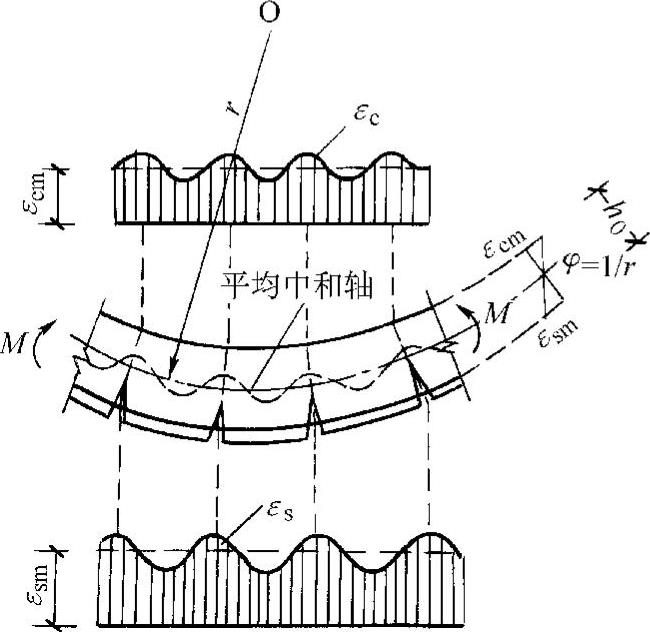
图9-9 梁纯弯区段内各截面应变及裂缝分布

ε_sm=ψε_s

式中 ψ——钢筋应变的不均匀系数；

ε_s——开裂截面钢筋的应变。

（2）压区混凝土的应变分布也是不均匀的，开裂截面应变较大，裂缝之间应变较小，但其波动幅度比钢筋应变波动的幅度要小。对压区混凝土也可建立如下关系：

ε_cm=ψ_cε_c （9-37）

式中 ε_cm——压区混凝土的平均应变；

ε_c——开裂截面混凝土的应变；

ψ_c——受压区边缘的混凝土应变不均匀系数。

（3）由于裂缝的影响，截面中和轴高度x_n也呈波浪形变化，开裂截面x_n小而裂缝之间截面x_n大。其平均中和轴高度用x_n表示，该截面称为平均截面。

（4）试验表明，平均应变ε_cm、ε_sm符合平截面假定，即沿截面平均应变呈直线分布。

基于以上的试验分析，可以推导出钢筋混凝土梁的刚度计算公式。

2.在荷载标准组合或准永久组合下受弯构件的短期刚度

由于本次规范修订将钢筋混凝土结构的挠度计算采用荷载准永久组合，而预应力混凝土结构的挠度计算仍采用荷载标准组合，且公式推导仍采用原规范的方法，即采用荷载标准组合，所以下面的推导仍采用荷载标准组合，仅在需要处注明荷载准永久组合的效应值。

由于平均应变符合平截面假定，由几何关系，即曲率和应变的关系，由图9-9和图9-10，可得平均曲率：

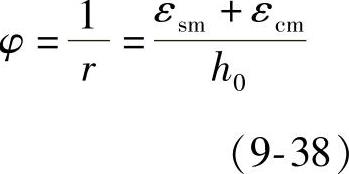
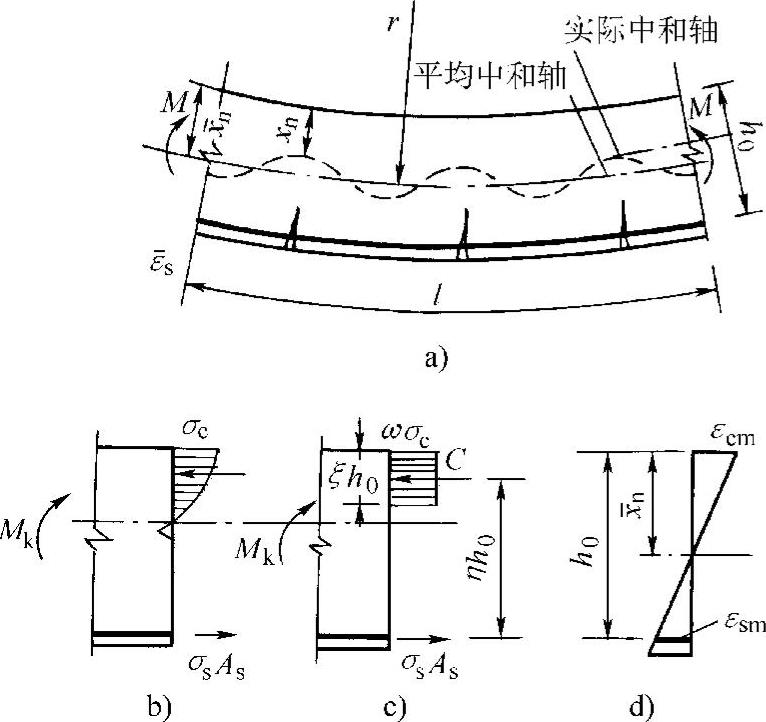
图 9-10

a）中和轴沿梁长的变化 b）裂缝截面实际应力分布 c）裂缝截面等效应力分布 d）平均截面应变分布

式中 r——平均曲率半径；

ε_sm——纵向受拉钢筋平均应变；

ε_cm——受压区边缘混凝土平均应变。

裂缝截面处的计算应力图形如图9-10所示。

由物理关系，即应力和应变关系，可得：

对裂缝截面，纵向受拉钢筋应变

对平均应变可按下列公式计算：

对受压区混凝土，考虑到混凝土的弹塑性变形，引用变形模量E′_c=ν_cE_c，ν_c为混凝土弹性特征系数，则对裂缝截面有

对平均截面

由平衡关系，即内力与应力间的关系：对开裂截面建立平衡方程式。开裂截面压区混凝土应力分布为曲线，如图9-10b。如用等效矩形图来代替，引入应力图形丰满度系数ω，其折算应力为ωσ_c；压区高度为：矩形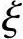h₀；T形（γ′_f+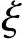）h₀，γ′_f为受压翼缘截面面积与腹板有效截面面积的比值，即γ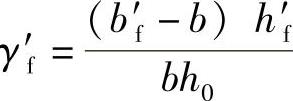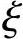；为裂缝截面处受压区高度系数，即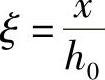。(www.xing528.com)

内力臂为_ηh₀，受压区应力合力为C，

C=ωσ_c（γ′_f+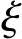）bh₀ （9-43）

对纵向受拉钢筋应力合力作用点取矩，得：

M_k=Cηh₀=ωσ_c（γ′_f+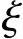）bh₀ηh₀

即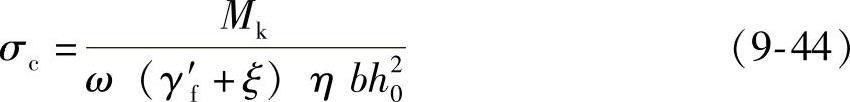

式中 M_k——按荷载标准组合计算的弯矩值。

对受压区压应力合力作用点取矩

M_k=σ_sA_sηh₀

即

将物理关系式（9-40）与式（9-42）代入几何关系式（9-38），可得

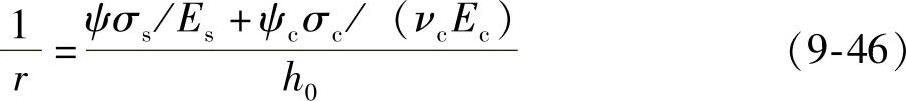
由材料力学可知，曲率1/r与刚度B_s有如下关系：

式中 B_s——荷载标准组合作用下的短期刚度。

于是可得

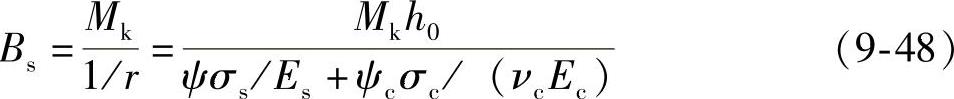
将式（9-44）、式（9-45）代入此式，可得

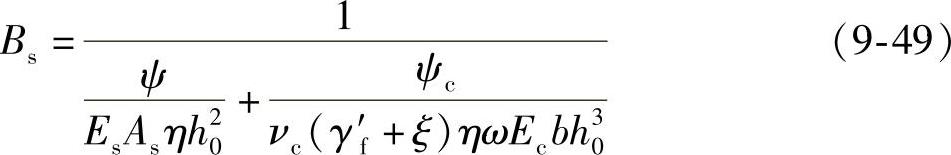
令α_E=E_s/E_c，ρ=A_s/（bh₀），ζ=ν_c（γ′_f+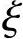）ηω/ψ_c

式中 α_E——钢筋与混凝土弹性模量之比；

ρ——纵向受拉钢筋配筋率；

ζ——混凝土受压区边缘平均应变综合系数，也可称为截面的弹塑性抵抗矩系数。

于是，式（9-49）可写为

这便是钢筋混凝土矩形、T形梁在使用阶段短期刚度的计算公式。

试验表明，受压区边缘混凝土平均应变综合系数ζ随荷载增大而减小，在裂缝出现后降低很快，而后逐渐缓慢，在使用荷载范围内则基本稳定。因此，对ζ的取值可不考虑荷载的影响。根据试验资料统计分析可得α_Eρ/ζ为（图9-11）：

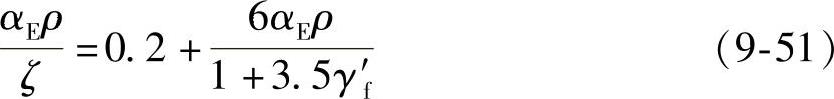
式中 ρ——纵向受拉钢筋配筋率，ρ=A_s/（bh₀）。

将式（9-51）代入式（9-50）及取η=0.87，可得受弯构件的短期刚度公式：

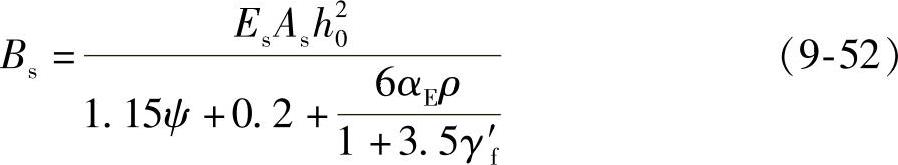
在荷载标准组合作用下，受压钢筋对截面刚度的影响不大，计算时可不考虑。如需考虑其影响，可将式（9-51）中的γ′_f改按下列公式计算：

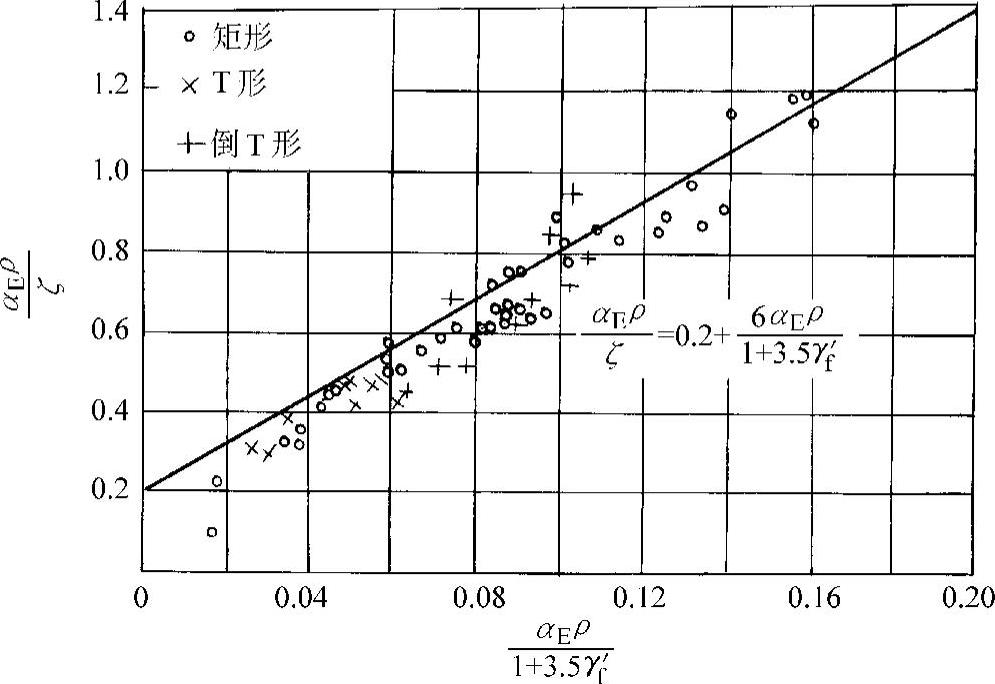
图9-11 参数α_Eρ/ζ的试验规律

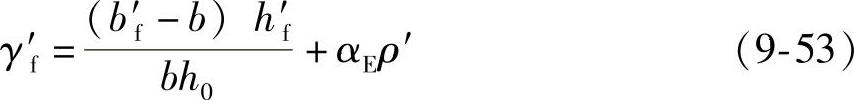
式中 ρ′——纵向受压钢筋配筋率，即ρ′=A′_s/（bh₀′）。