钢筋混凝土梁刚度变化研究

由材料力学可知，对于均质弹性材料简支梁，在均布荷载作用下，其跨中的挠度为

其中EI为梁的抗弯刚度，M为梁中最大弯矩。上式可统一写成

式中 C——与荷载类型和支承条件有关的系数；

B——梁的抗弯刚度。

当梁为均质线弹性材料时，C、B是常数，挠度f与弯矩M成线性关系，如图9-8中的OD直线。对于钢筋混凝土梁，由于材料的非弹性性质和受拉区裂缝的发展，梁的刚度不是常数，而是随着荷载的增加不断降低（图9-8）。由图9-8的配筋适量的钢筋混凝土梁的弯矩M与挠度f的关系可以看出，M-f曲线可以分为三个阶段。

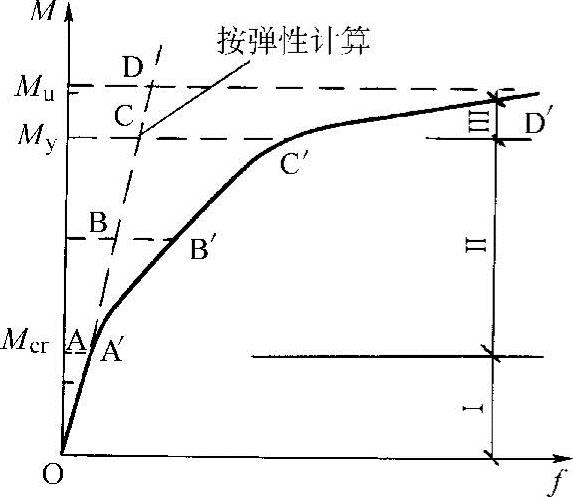
图9-8 适筋梁的实测M-f关系曲线（实线）(www.xing528.com)

第Ⅰ阶段是裂缝出现以前。这一阶段梁的性能接近弹性，M与f基本成直线关系。临近裂缝出现时，M-f关系由直线转向曲线，这是由于拉区混凝土塑性变形的发展，使梁的刚度有所降低，如图9-8中的OA′这一阶段梁的短期刚度可按下式计算：

B_s=0.85E_cI₀ （9-36）

式中 E_c——混凝土的弹性模量；

I₀——换算截面的惯性矩。

第Ⅱ阶段是裂缝出现以后到受拉区钢筋屈服以前。裂缝出现以后，M-f关系曲线发生转折，梁的刚度有明显的降低，如图9-8中的A′C′。这主要是由于受拉区混凝土裂缝开展使混凝土逐步推出工作，以及压区混凝土塑性变形所引起的。正常使用阶段的挠度验算，主要指这个阶段的验算。

当受拉区钢筋屈服以后，M-f关系曲线出现第二个转折点，进入第Ⅲ阶段（如图9-8中的C′D′）。这一阶段，当M增加很少甚至不增加时，f很快增大，说明刚度急剧降低，处于承载力的极限状态。

由以上分析可见，钢筋混凝土梁的抗弯刚度不是一个始终不变的常数，而是随着荷载的增加而不断降低。由于对普通钢筋混凝土梁，在使用荷载作用下，绝大多数属于第Ⅱ阶段，所以下面着重讨论这一阶段梁的刚度变化规律。