9.2.3平均裂缝宽度计算方法及应用

裂缝开展后，由图9-4可知，在钢筋重心处的裂缝宽度w_cr是裂缝间距区段内钢筋与混凝土的伸长量之差，即

w_cr=ε_sml_cr-ε_cml_cr （9-14）

图9-4 平均裂缝宽度计算模式

式中 ε_sm、ε_cm——钢筋和混凝土的平均拉应变。

设裂缝处的钢筋应变为ε_s，则由9.2.2节可知，钢筋的平均应变ε_sm显然比裂缝截面的钢筋应变ε_s来得小。这是因为在裂缝之间混凝土仍然能承担拉力的缘故。用受拉钢筋应变不均匀系数ψ来表示裂缝之间因混凝土承受拉力而对钢筋应变所引起的影响，它是钢筋平均应变ε_sm对裂缝截面钢筋应变ε_s的比值，即ψ=ε_sm/ε_s。实质上它反映了裂缝间拉区混凝土参与受力的程度。显然ψ是不会大于1的，ψ值越小，表示混凝土参与承受拉力的程度越大；ψ值越大，表示混凝土参与承受拉力的程度越小，各截面中钢筋的应力就比较均匀；当ψ=1时，表示混凝土完全脱离工作。

由于

且由于本次规范修订w_max仍采用2002版规范的形式，所以下面推导仍采用2002版规范的形式，仅在最后将标准荷载组合改为准永久荷载组合。

这样

令

则裂缝宽度的式（9-14）可写为

α_c为裂缝间混凝土自身伸长对裂缝宽度的影响系数，它与配筋率ρ_te、混凝土保护层厚度c等有关，但实验表明，ε_cm要比ε_sm小得多，且其变化幅度不大，根据实测，α_c可取0.85。

由式（9-18）可见，在α_c取为0.85，且裂缝间距已由上节求得后，裂缝宽度就主要取决于裂缝截面的钢筋应力σ_sk和裂缝间纵向受拉钢筋应变不均匀系数ψ。

1.ψ值

ψ=ε_sm/ε_s，显然ψ是一个小于1的系数，它反映了裂缝间受拉混凝土参与工作的程度。随着外力的增加，裂缝截面的钢筋应力σ_sk随之增大，钢筋与混凝土之间的粘结逐步被破坏，受拉混凝土就逐渐退出工作。因此ψ值必然与σ_sk有关。当最终受拉混凝土全部退出工作时，ψ值就趋近于1.0。影响ψ的因素很多，除钢筋应力外，还与混凝土抗拉强度f_tk、配筋率ρ、钢筋与混凝土间的粘结性能、荷载作用的时间和性质有关。f_tk愈大，混凝土参与受拉程度就愈大，ψ值愈小；ρ值愈小，说明周围混凝土截面相对愈大，则混凝土参与受拉的程度将愈大，因而ψ愈小。考虑到混凝土参与受力主要是在钢筋周围一定范围内的混凝土（称为有效受拉区混凝土面积）起作用，因而ψ值仅与有效受拉区混凝土面积范围内配筋率ρ_te有关。准确地计算ψ值是十分复杂的，目前大多是根据试验资料给出半理论半经验的ψ值计算公式。

试验结果和理论分析表明（图9-5），纵向受拉钢筋应变不均匀系数ψ可按下列公式计算：

式中 ω₁——系数，与钢筋和混凝土的握裹力有一定关系，对光圆钢筋，ω₁则接近1.1。根据偏拉、偏压构件的试验资料，以及为了与轴心受拉构件的计算公式协调，将ω₁统一为1.1；

M_cr——混凝土截面的开裂弯矩值；

M_k——按荷载标准组合计算的弯矩值。

M_cr、M_k可按下列公式计算：

M_cr=0.8[0.5bh+（b_f-b）h_f]η₂hf_tk （9-20）

M_k=A_sσ_skηh₀ （9-21）

式中 f_tk——混凝土抗拉强度标准值；

η₂——受拉区混凝土应力合力作用点至受压区混凝土应力合力作用点的距离与截面高度h的比值；

η——纵向受拉钢筋应力合力作用点至受压区混凝土应力合力作用点的距离与截面有效高度h₀的比值。

图9-5 ψ—M_cr/M_k关系

经分析，可近似取η₂/η=0.67，又近似取h/h₀=1.1，可得

新规范对钢筋混凝土结构取准永久荷载组合，所以σ_sk改为σ_sq；

对预应力混凝土结构仍取σ_sk，即按荷载标准组合计算。

式中 ψ——裂缝间纵向受拉钢筋应变不均匀系数；当ψ<0.2时，取ψ=0.2；当ψ>1时，取ψ=1；对直接承受重复荷载的构件，取ψ=1。

2.钢筋应力σ_sq

对于轴心受拉构件，在裂缝截面，整个截面拉力全由钢筋承担，故在使用荷载下的钢筋应力σ_sq可由下式求得

(www.xing528.com)

式中 N_q——按荷载准永久组合计算的轴向力值。

对于受弯构件，根据式（9-21），当近似取η=0.87，并将M_k用M_q替换，则可得

M_q——按荷载准永久组合计算的弯矩值。

对于偏心受拉构件，当轴向拉力作用在钢筋A_s和A′_s的截面重心之间时，对A′_s截面重心取矩，可得

式中 N_q——按荷载准永久组合计算的偏心拉力值；

e′——轴向拉力作用点至受压区或受拉较小边纵向钢筋合力点的距离。

当轴向拉力作用在较大受拉边钢筋A_s的截面重心以外时，对A′_s截面重心取矩，且近似取z=h₀-a′_s，也可得式（9-25）。

对于偏心受压构件，裂缝截面的应力图形如图9-6所示。对受压区合力点取矩，可得

z=ηh₀ （9-27）

式中 N_q——按荷载准永久组合计算的偏心压力；

e——轴向力N_q至纵向受拉钢筋截面重心的距离；

z——纵向受拉钢筋合力点至截面受压区合力点的距离，且不大于0.87h₀；

η——纵向受拉钢筋应力合力作用点至受压区应力合力作用点的距离与截面有效高度的比值。

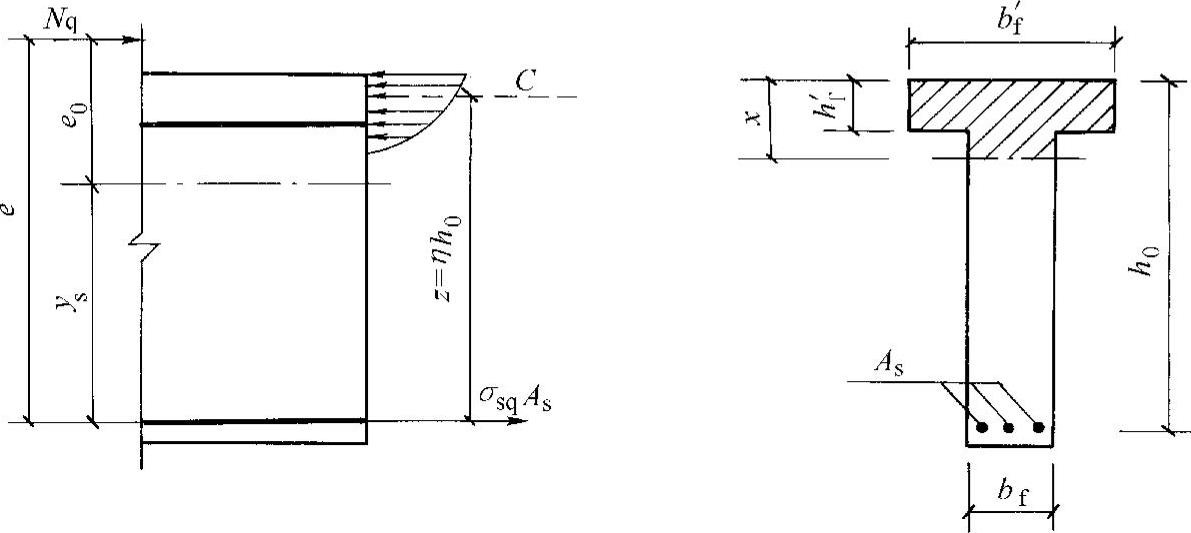
图9-6 偏心受压构件裂缝截面的应力

由式（9-26）可见，求解η是计算钢筋应力的关键。通过电算分析表明，η可按下列拟合公式计算：

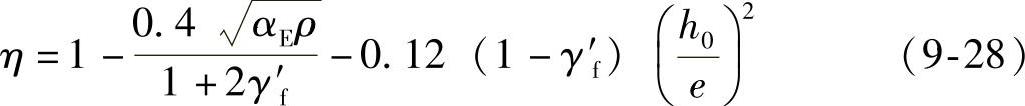
式中 α_E——钢筋弹性模量与混凝土弹性模量的比值；

ρ——纵向受拉钢筋配筋率；

γ′_f——受压翼缘截面面积与腹板有效截面面积的比值；

e——轴向压力作用点至纵向受拉钢筋截面重心的距离。

式（9-28）与理论分析结果的比较如图9-7所示，可见其拟合程度尚好。

上式可进一步简化为

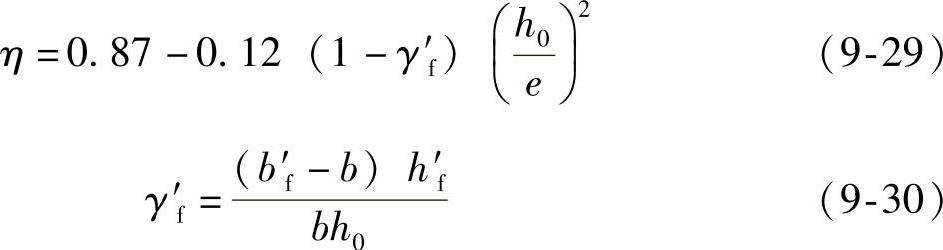
试验表明，在正常使用阶段，当l₀/h≤14时，偏心受压构件的侧向挠度不大，计算裂缝宽度时可不考虑侧向挠度的影响。当l₀/h>14时，则应考虑侧向挠度的影响，亦即应将轴向力偏心矩e₀（即M_k/N_k）乘以偏心矩增大系数η_s。η_s可近似按下列公式计算：

图9-7 理论分析与拟合公式比较

e=η_se₀+y_s （9-32）

式中 l₀——偏心受压构件的计算长度；

y_s——截面重心至纵向受拉钢筋合力点的距离。

当α_c、l_cr、σ_sk及ψ值求得后代入式（9-18）就可求得平均裂缝宽度w_cr。