钢筋混凝土结构：9.2.2裂缝间距lcr分析

图9-2所示为一轴心受拉构件，设混凝土出现第一条裂缝后，取裂缝截面1-1至即将出现第二条相邻裂缝的截面2-2的一段混凝土l为脱离体。在裂缝处，混凝土应力为零，钢筋应力为σ_s1；在距裂缝为l处，混凝土应力上升到f_t，钢筋应力降低为σ_s2，如图9-2所示。由平衡条件得

A_sσ_s1=A_sσ_s2+A_cf_t

或 A_sσ_s1-A_sσ_s2=A_cf_t （9-5）

式中 A_s、A_c——钢筋与混凝土的截面积。

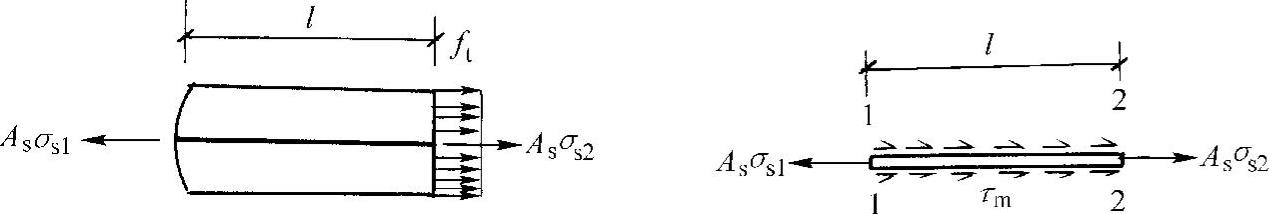
图9-2 混凝土脱离体的应力图形

取截面1-1至截面2-2钢筋段为脱离体，钢筋两端的不平衡力由粘结力平衡。设l段内的平均粘结应力为τ_m，钢筋的总周长为u，则由平衡条件可得

A_sσ_s1-A_sσ_s2=τ_mul （9-6）

对比式（9-5）与式（9-6），可得

A_cf_t=τ_mul

或

若配筋由n根直径为d的钢筋组成，则其总周长为u=nπd，总面积A_s=nπd²/4，从而可得u=4A_s/d，代入式（9-7），并取ρ=A_s/A_c可得

考虑裂缝的平均间距为1.5l，故

由试验可知，混凝土的f_t与τ_m近乎成正比，因此，当混凝土强度和钢筋的外形特征给定时，裂缝的平均间距将随比值d/ρ而变化。

试验表明，混凝土保护层厚度对裂缝间距也有影响，保护层愈大，裂缝间距也愈大。另外，考虑到混凝土参于受拉主要与有效受拉混凝土面积有关，所以用ρ_te代替式（9-9）中的ρ。

以上分析是对轴心受拉构件进行的，对于受弯构件也可得出类似的结论。根据以上分析，《规范》引进保护层厚度c和d/ρ_te两个变量，并考虑纵向受拉钢筋的相对粘结特征，对试验资料进行统计分析后，建议采用下列公式计算平均裂缝间距：

对轴心受拉构件：(www.xing528.com)

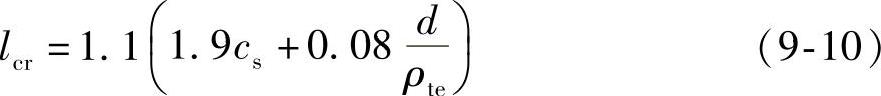
对受弯、偏心受拉和偏心受压构件：

式中 c_s——最外层纵向受拉钢筋外边缘至受拉区底边的距离（mm），当c_s<20mm时，取c_s=20mm；当c_s>65mm时；取c_s=65mm；

ρ_te——按有效受拉混凝土截面面积计算的纵向受拉钢筋的配筋率。在最大裂缝宽度计算中，当ρ_te<0.01时，取ρ_te=0.01。

A_te——有效受拉混凝土截面面积；对轴心受拉构件，取构件截面面积；对受弯、偏心受压和偏心受拉构件，取A_te=0.5bh+（b_f-b）h_f，此处，b_f、h_f为受拉翼缘的宽度、高度，如图9-3所示；

A_s——受拉区纵向钢筋截面面积；

d——钢筋直径。当配置不同钢种、不同直径的钢筋时，式中d应改为等效直径d_eq，按式（9-13）进行计算确定，其中考虑了钢筋混凝土和预应力混凝土构件配置不同的钢种、钢筋表面形状以及预应力钢筋采用先张法或后张法（灌浆）等不同的施工工艺。

式中 d_eq——受拉区纵向钢筋的等效直径（mm）；

d_i——受拉区第i种纵向钢筋的公称直径（mm）；

n_i——受拉区第i种纵向钢筋的根数；

ν_i——受拉区第i种纵向钢筋的相对粘结特性系数，按表9-3采用。

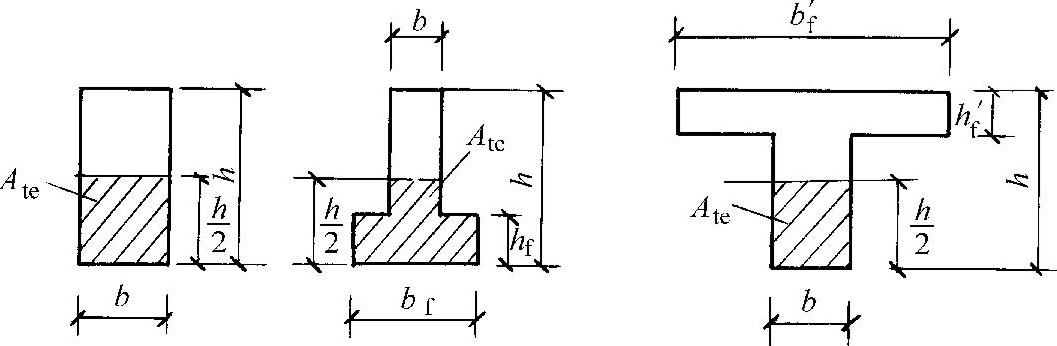
图 9-3

表9-3 钢筋的相对粘结特性系数

注：对环氧树脂涂层带肋钢筋，其相对粘结特性系数应按表中系数的0.8倍取用。