小偏心受拉构件正截面承载力计算-钢筋混凝土结构

小偏心受拉构件的受力特点是：混凝土开裂后，裂缝贯穿整个截面，全部轴向拉力N由纵向钢筋承受。当纵向钢筋达到屈服强度时，截面即达到极限状态。如图8-4所示，由内力平衡条件得

N=f_yA_s+f_yA′_s （8-10）

分别对A_s及A′_s的合力点取矩得

Ne′=f_yA_s（h₀-a′_s） （8-11）

Ne=f_yA′_s（h₀-a′_s） （8-12）

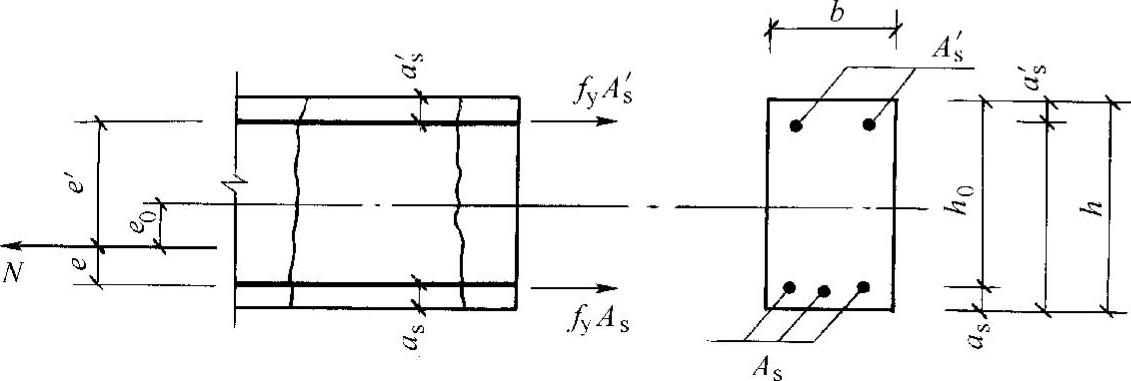
图8-4 小偏心受拉构件承载力计算图

其中

则可得

若将e和e′值代入以上二式，并取M=Ne₀则得

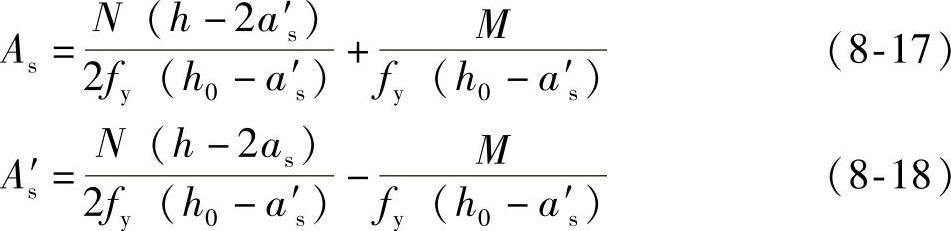
上式第一项代表轴向力N所需的配筋，第二项代表弯矩M的影响。M增加了A_s的用量而降低了A′_s的用量。因此设计中同时有几组不同的荷载组合（N，M）时，应按最大N和最大M的荷载组合计算A_s值，而按最大N和最小M的荷载组合计算A′_s值。

当对称配筋时，远离偏心一侧的钢筋A′_s达不到屈服，在设计时可按式（8-15）计算，即

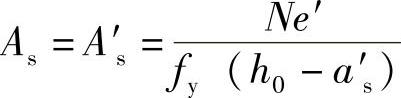
其中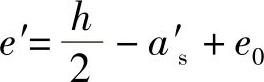

【例8-1】 一钢筋混凝土偏心受拉构件，截面为矩形b×h=200mm×400mm，a_s=a′_s=35mm，需承受轴向拉力设计值N=450kN，弯矩设计值M=100kN·m，混凝土强度等级C20（f_c=9.6MPa），钢筋为HRB335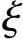，_b=0.55，f_y=300MPa。求：纵向钢筋截面面积A_s及A′_s。

【解】 （1）判别大小偏心情况

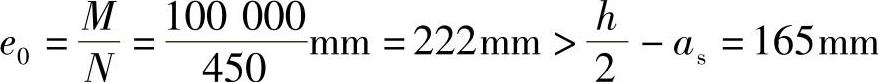
属于大偏心受拉。(https://www.xing528.com)

（2）求A′_s

取x=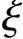_bh₀=0.55×365mm=201mm

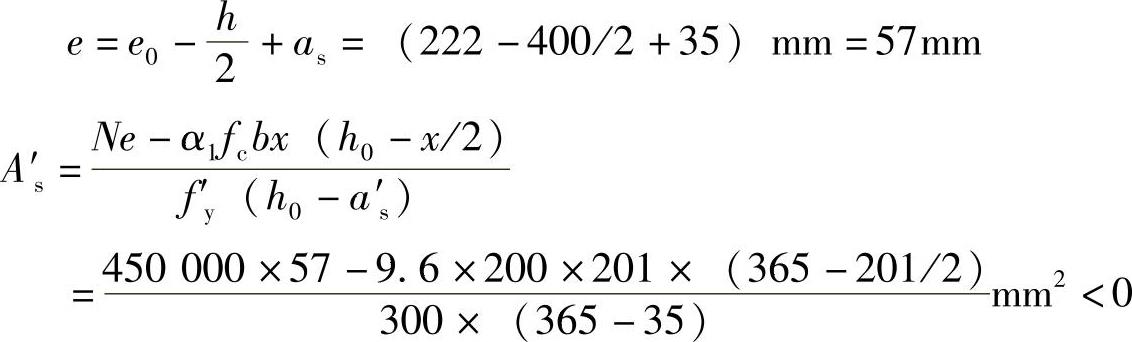
A′_s按最小配筋率配置，取

A′_s=ρ_minbh=0.002×200×400mm²=160mm²

选用A′_s为210；A′_s=157mm²

（3）求A_s

由式（8-3）得

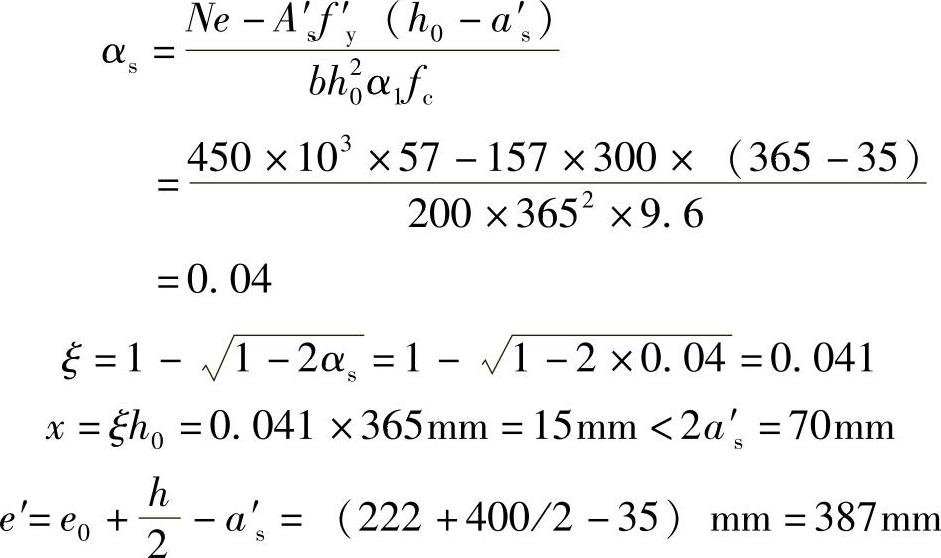
由式（8-8）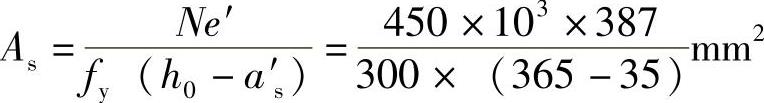

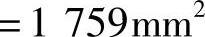
实配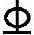225+2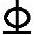22，A_s=1742mm²

【例8-2】 若构件截面尺寸、材料和【例8-1】相同，而承受轴向拉力设计值N=450kN，弯矩设计值M=60kN·m。求：纵向钢筋截面面积A_s及A′_s。

【解】 （1）判别大小偏心情况

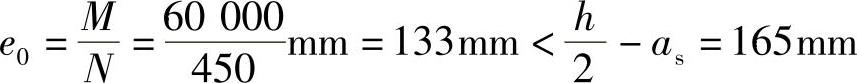
属于小偏心受拉。

（2）求A_s及A′_s

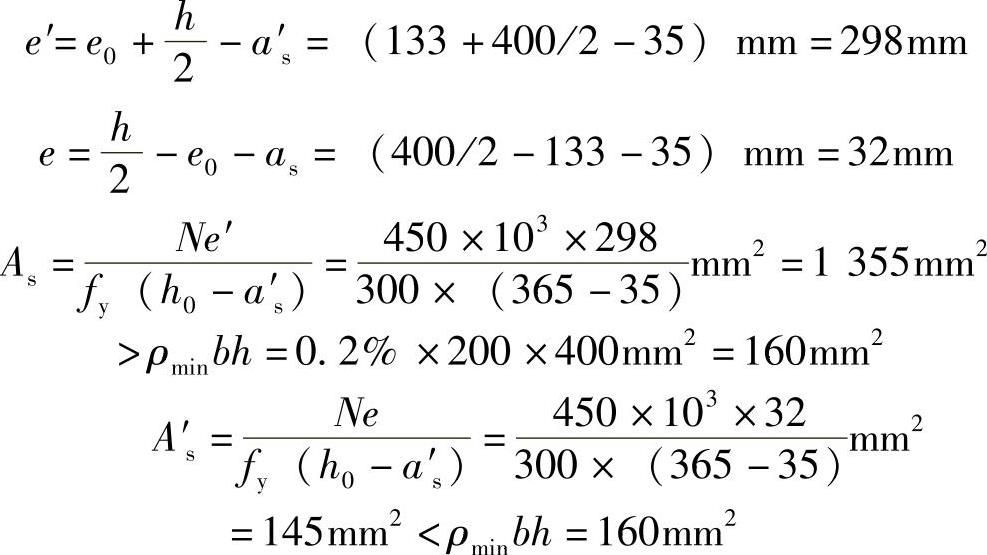
实配A_s一侧选用325（A_s=1473mm²）

A′_s一侧选用210（A′_s=157mm²）