8.3大偏心受拉构件承载力计算，钢筋混凝土结构

当纵向力作用在A_s合力点及A′_s的合力点以外时，属于大偏心受拉构件。

大偏心受拉构件的受力特点是：随着轴向拉力N的增加，破坏时在截面拉应力较大的一侧混凝土首先开裂，但裂缝并不贯穿整个截面，其破坏形态和大偏心受压构件相似，也是由于受拉钢筋首先屈服，随后受压区混凝土被压碎。计算时所采用的应力图形亦与大偏心受压构件相似，因此其计算公式及计算步骤均与大偏心受压构件相似，只是轴向力N的方向和大偏心受压构件相反。

图8-3所示为矩形截面大偏心受拉构件的受力情况。构件破坏时钢筋A_s及A′_s应力都达到屈服强度，受压区混凝土应力取用α₁f_c，应力分布按矩形图计算，则由内力平衡条件得

N=f_yA_s-f′_yA′_s-α₁f_cbx （8-2）

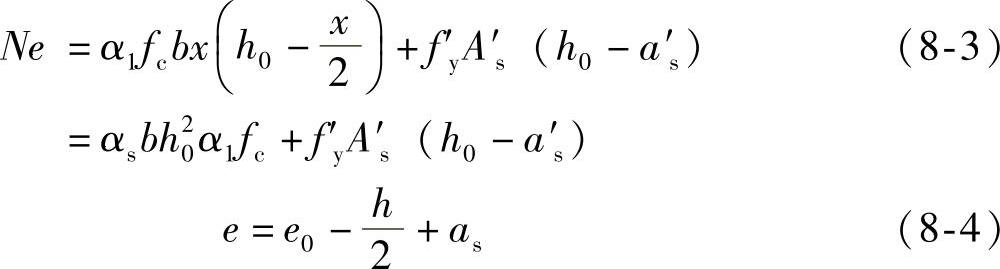
上述公式应符合x≤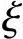_bh₀及x≥2a′_s的适用条件。

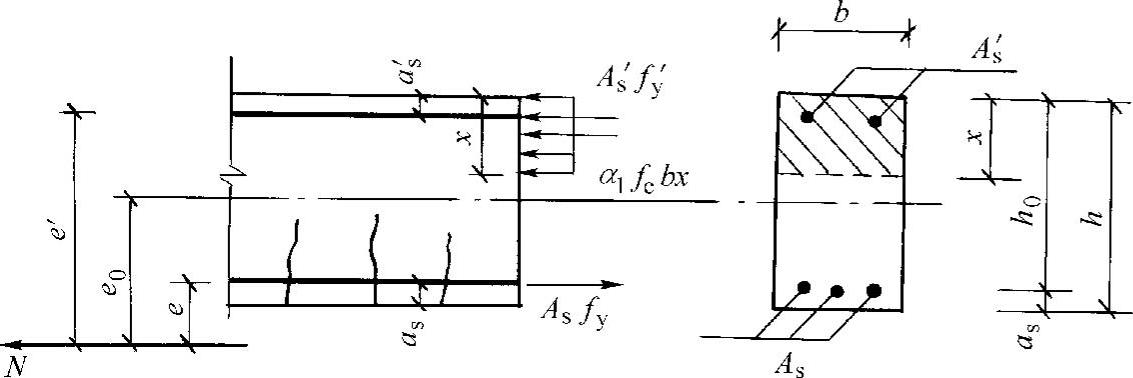
图8-3 大偏心受拉构件承载力计算图

在设计时为了使钢筋总用量（A_s+A′_s）最少，与偏心受压构件一样，应取受压区高度x=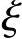_bh₀，代入式（8-3）及式（8-2）可得

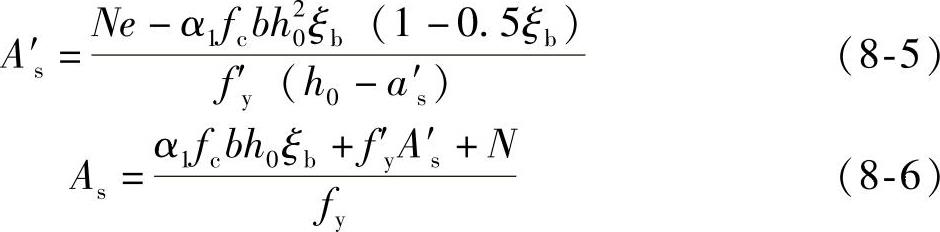
若按式（8-5）求得的A′_s<ρ_minbh（包括为负值）则可先按构造要求或最小配筋率配置A′_s，变为已知A′_s求A_s的情况。

当已知A′_s求A_s时，可由式（8-3）求出α_s

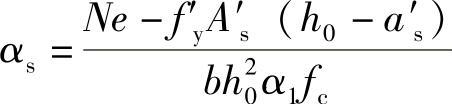(https://www.xing528.com)

然后用下式求出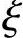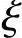，=1-1-2α_s

x=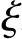h₀，当2a′_s≤x≤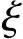_bh₀则由式（8-2）可求出A_s

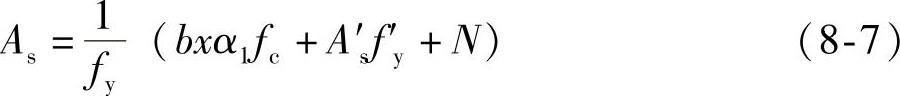
与偏心受压构件相比，仅是N为“+”号，由于轴向拉力的存在增加了受拉钢筋的数量。

若x<2a′_s，可以近似地假定受压区混凝土承担的压力与受压钢筋承担的压力重合，则对受压钢筋合力中心取矩可得：

Ne′=f_yA_s（h₀-a′_s） （8-8）

式中 e—′——轴向拉力N作用点到受压钢筋A′_s的距离。

由式（8-8）得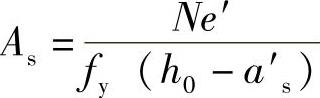

当构件的截面尺寸、材料和纵向钢筋均为已知，要复核截面的承载力时，可联立式（8-2）、式（8-3）求解，先解出x，根据x值的大小，来决定N值的解法。当2a′_s≤x≤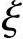_bh₀时，用式（8-2）求N；当x<2a′_s时，用式（8-8）求N。

当采用对称配筋时，由于A_s=A′_s，f_y=f′_y，代入式（8-2）后，求得的x值必为负值，属x<2a′_s的情况，则可用式（8-8）进行配筋计算或承载力校核。