矩形截面偏心受压构件正截面承载力计算基本公式

1.基本假定

钢筋混凝土偏心受压构件正截面承载力计算的基本假定与受弯构件完全相同，参见第4章。

2.大偏心受压构件基本计算公式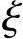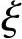（≤_b）

大偏心受压构件破坏时，其受拉及受压纵向钢筋均能达到屈服强度，受压区混凝土应力为抛物线形分布，如图7-21a所示。为简化计算，同样可以用矩形应力分布图形来代替实际的应力分布图（图7-21b），混凝土压应力取轴心抗压强度设计值f_c乘以系数α₁，受压区高度为x，则根据纵向力的平衡和对受拉钢筋合力点的力矩的平衡可得

N=α₁f_cbx+f′_yA′_s-f_yA_s （7-16）

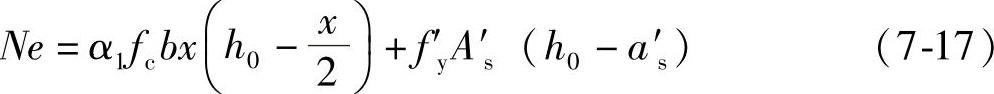
式中 N——轴向力设计值；

e——轴向力作用点至受拉钢筋A_s合力点之间的距离；

e_i=e₀+e_a （7-19）

e_i——初始偏心距；

e₀——轴向压力对截面重心的偏心距，取为M/N，当需要考虑二阶效应时，M应乘以弯矩增大系数η_ns和偏心距调节系数C_m；

e_a——附加偏心距，其值取20mm和偏心方向截面最大尺寸的1/30两者中的较大值。

基本公式的适用条件为：

1）为保证受拉钢筋A_s达到屈服，应满足x≤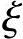_bh₀

2）为保证构件破坏时受压钢筋A′_s达到屈服，应满足x≥2a′_s

或 z≤h₀-a′_sz为受压区混凝土合力与受拉钢筋合力之间的内力臂。

3.小偏心受压构件基本计算公式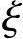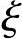（>_b）

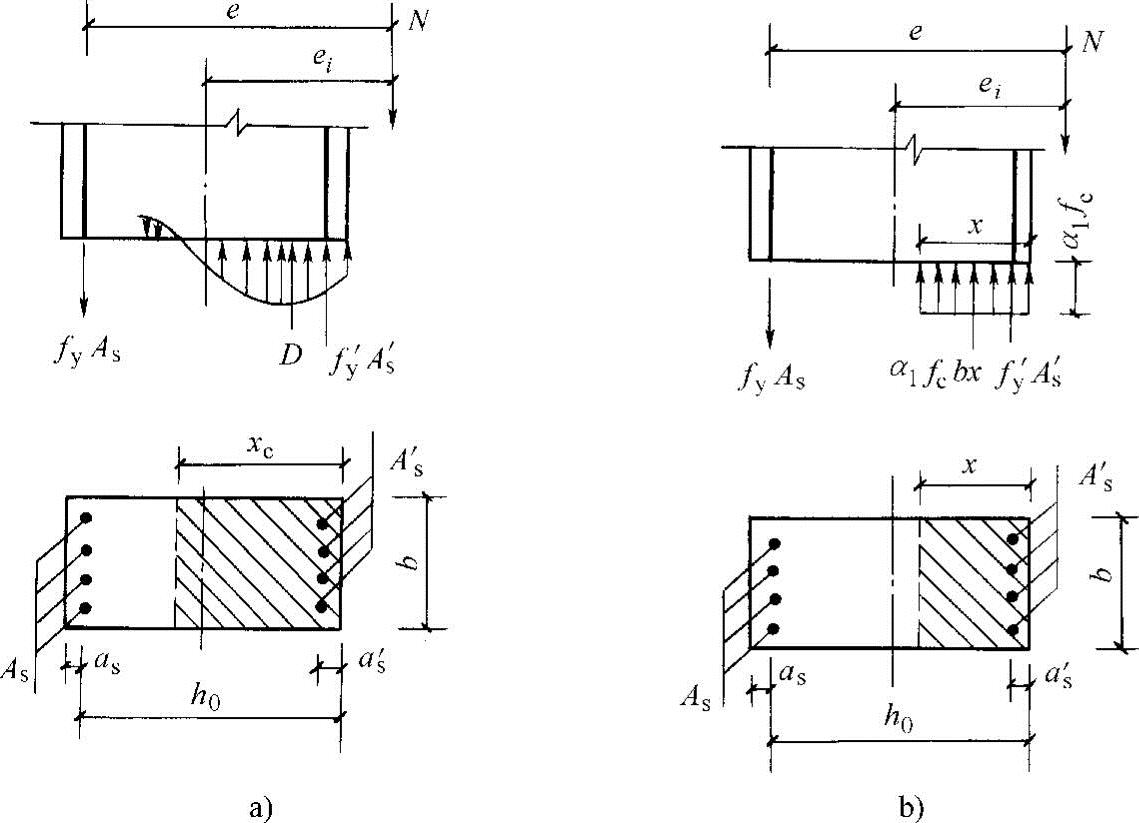
图7-21 大偏心受压应力计算图形

a）实际应力分布图 b）计算图形

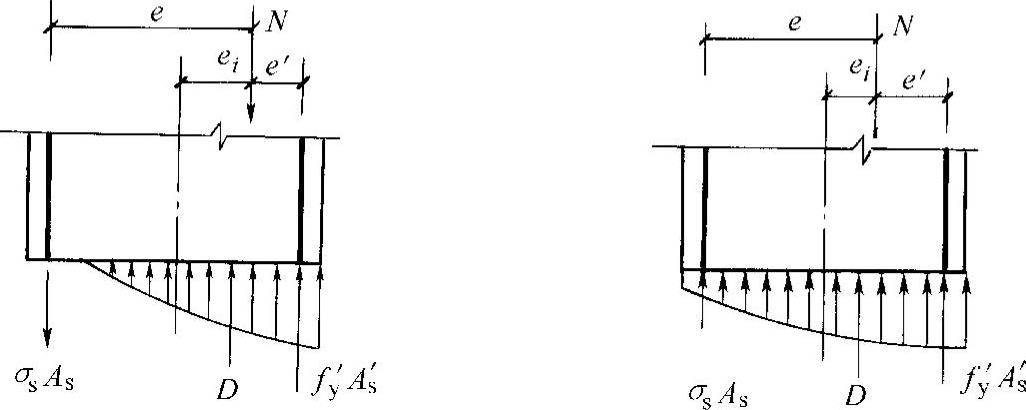
小偏心受压构件破坏时的应力分布图形可能是全截面受压或截面部分受压、部分受拉。离纵向力较近一侧的受压钢筋A′_s，一般都能达到屈服强度；而远离纵向力一侧的钢筋A_s则可能受压或受拉，其应力为σ_s，往往都未达到屈服强度。小偏心受压构件截面实际应力分布图形如图7-22所示，计算应力图形如图7-23所示。根据纵向力的平衡和对受拉钢筋（或受压较小钢筋）合力点的力矩平衡可得

(www.xing528.com)

图7-22 小偏心受压实际应力分布图

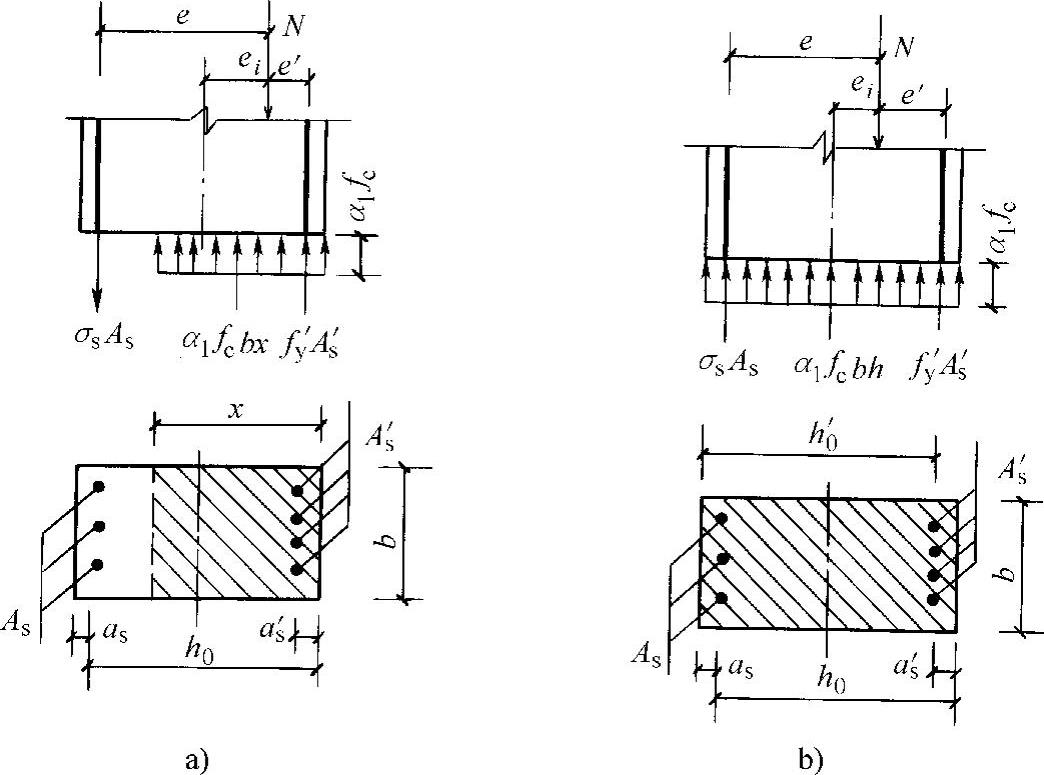
图7-23 小偏心受压计算图形

a）A_s受拉 b）A_s受压

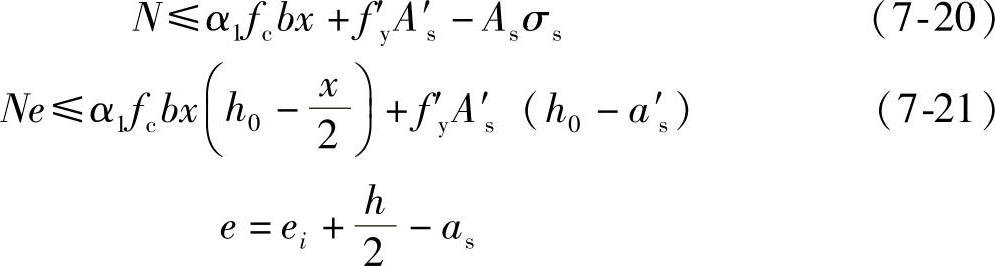
式中 x——受压区高度，当x>h时，取x=h；

σ_s——远离纵向力一侧钢筋的应力。

钢筋应力σ_s可用下面二种方法确定：

（1）用平截面假定条件确定σ_s值

由图7-24，根据基本假定，取x=β₁x_c，当构件压坏时取ε_c=ε_cu，同时取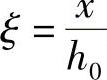则得

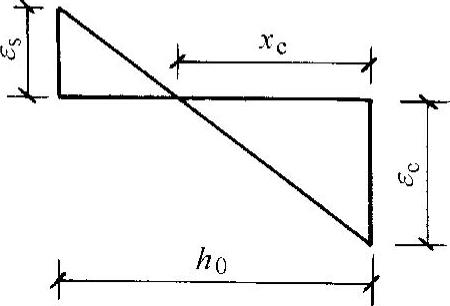
图7-24 截面应变

当σ_s>0时，A_s受拉；反之，当σ_s<0时，A_s受压。σ_s、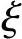关系如图7-25所示。

（2）σ_s的简化计算式

如图7-25所示，式（7-22）中σ_s与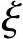的关系为双曲线函数，而σ_s值对小偏心受压正截面承载力影响很小，因此采用如下简化公式，用直线方程代替双曲线方程。

当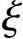=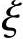_b时，即大、小偏压分界，取σ_s=f_y；当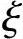=β₁，即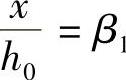，x=β₁x_c，则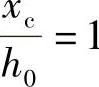，此时中和轴高度x_c=h₀，故取σ_s=0；通过以上两点可得σ_s—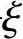的线性方程为

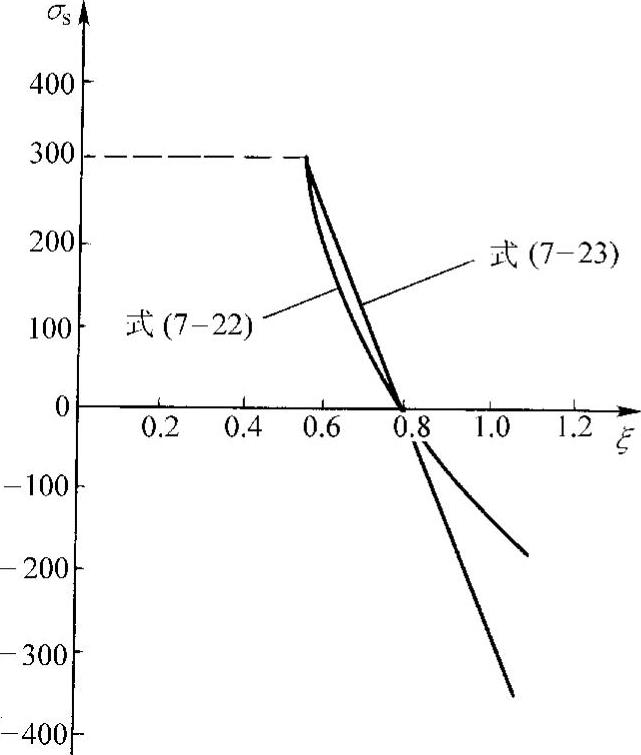
图7-25 σ_s—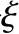关系图

式（7-23）与式（7-22）相比，当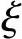在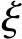_b和0.8之间变化时，两式求得的σ_s相差很小，当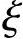值较大时（如在0.9～1.1）则用两式求出的σ_s相差较大。但应用式（7-23）的最大好处是在配筋计算时，可以降低方程的次数，避免求解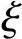的高次方程。