钢筋混凝土结构：考虑偏心受压构件的纵向弯曲和二阶效应

建筑结构或构件受到轴向压力会产生弯曲。建筑结构的二阶效应泛指作用在结构上的重力或构件中的轴向压力在产生了层面位移和挠曲变形后的结构或构件中引起的附加变形和相应的附加内力，包括结构整体的侧移二阶效应（P—Δ效应）和受压构件的挠曲效应（P—δ效应）两部分（图7-16a）。该图为有侧移结构，柱两端的附加弯矩为零，且比较大，一般考虑二阶效应后的最大弯矩仍出现在柱端。

对于图7-16b所示的钢筋混凝土柱，其计算简图可简化为图7-16c，即两端铰支且两端偏心距相等的“标准偏压柱”。该柱为无侧移柱，因柱端无侧移，故二阶效应只有P-δ效应，即纵向弯曲的影响。在初始偏心距为e₀的轴向压力N的作用下产生纵向弯曲，柱高度中点处的挠度为f₁。柱的长细比（l₀/h）不同，纵向弯曲的影响程度也不同。对于长细比较小的柱，即所谓“短柱”，由于纵向弯曲的影响较小，在设计时一般可忽略不计。对于长细比较大的柱，即所谓“长柱”，纵向弯曲的影响在设计时必须予以考虑，因为纵向弯曲将导致承载力的降低。对于长细比很大的柱，即所谓“细长柱”，因为纵向弯曲可能会引起柱“失稳”破坏，在设计中宜尽量避免出现“细长柱”。对于“短柱”、“长柱”和“细长柱”很难确定截然的界限，我国原《混凝土结构设计规范》（GB50010—2002）规定对于长细比l₀/i≤17.5（或l₀/h≤5）的钢筋混凝土柱可以视为“短柱”而不考虑纵向弯曲的影响。对于“长柱”和“细长柱”则未规定界限，就一般情况而言，柱的长细比宜控制在30以内，即对于l₀/h=5～30的柱可视为“长柱”。“长柱”的破坏仍属“材料破坏”，即钢筋和混凝土可以发挥其强度。

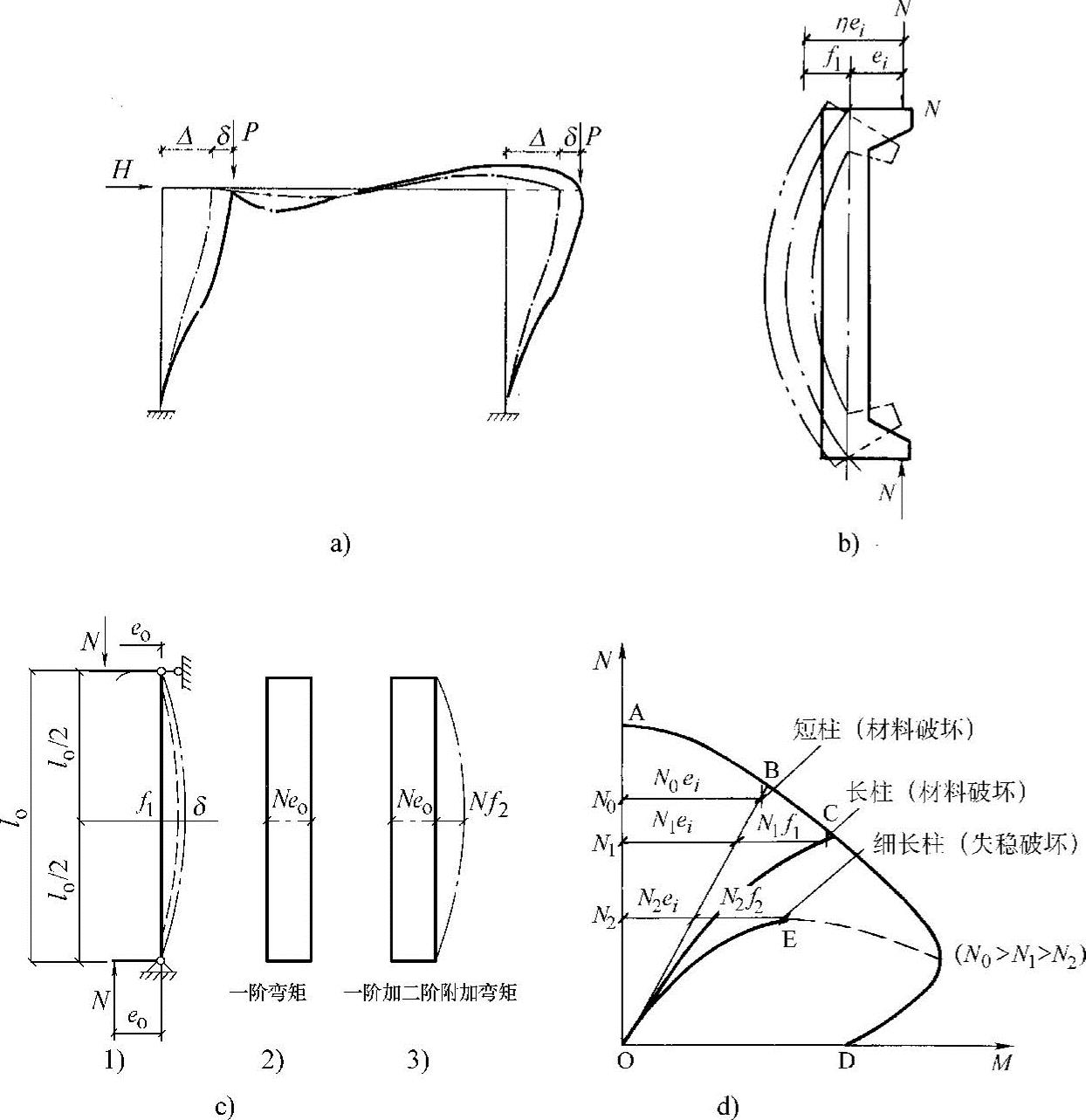
图7-16 二阶效应和长短柱的碳标形态到破坏的N—M关系

新《规范》（GB50010—2010）根据国外相关文献资料、规范以及近期国内对不同杆端弯矩比、不同轴压比和不同长细比的杆件进行计算验证的结果，给出了可以忽略杆件自身挠曲产生的P—δ效应影响的条件为：弯矩作用平面内截面对称的偏心受压构件，当同一主轴方向的杆端弯矩比不大于0.9且轴压比不大于0.9时，若构件的长细比满足式（7-7a）的要求，可不考虑轴向压力在该方向挠曲杆件中产生的附加弯矩影响。

l_c/i≤34-12（M₁/M₂） （7-7a）

式中 M₁、M₂——已考虑侧移影响的偏心受压构件两端截面按结构弹性分析确定的对同一主轴的组合弯矩设计值，绝对值较大端为M₂，绝对值较小端为M₁，当构件按单曲率弯曲时，M₁/M₂取正值，否则取负值；

l_c——构件的计算长度，可近似取偏心受压构件相应主轴方向上下支撑点之间的距离；

i——偏心方向的截面回转半径。

图7-16d给出了截面尺寸相同、材料强度及配筋相同、初始偏心距e_i相同，仅柱的长细比不同的三根柱，从加载到破坏的示意图。图中ABCD是构件发生材料破坏时的M和N相关图。

OB代表短柱从加载到破坏的过程，略去纵向弯曲的影响，e_i保持常量。

M=Ne_i

上式中的弯矩Ne_i是随着N值的增大而成线性关系，Ne_i称为一阶弯矩。当纵向力N增至N₀时，此时弯矩M=N₀e_i，在N₀和M的组合作用下柱发生“材料破坏”。

曲线OC代表长柱从加载到破坏的过程。由于长细比较大，纵向弯曲的影响不可忽略不计，柱产生侧向挠度f，偏心距由e_i增至e_i+f（见图7-16b），此时M=N（e_i+f）=Ne_i+Nf，由侧向挠度产生的弯矩Nf值是随着N及f值的增大而增大，故称二阶弯矩。对于长柱而言侧向挠度f是随着纵向力N的加大而不断非线性增加的，所以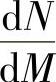是变数，在加载后期，纵向压力的稍许增加都会引起二阶弯矩的迅速增加。当纵向压力增至N₁时，弯矩M=N₁（e_i+f₁），在N₁和M的组合作用下，柱仍发生了“材料破坏”。

曲线OE代表长细比很大的“细长柱”从加载到破坏的过程。由于长细比很大，在较小的纵向压力作用下，柱已经产生较大的侧向挠度，在没有达到M、N的材料破坏关系曲线ABCD前，由于微小的纵向力增量ΔN可引起不收敛的弯矩M的增加而破坏，即所谓“失稳破坏”，曲线OE代表了这种类型的破坏，在E点的承载力已达最大，但此时截面内的钢筋应力并未达到屈服强度，混凝土也未达到受压强度值。

从图7-16d中还可看出，这三根柱虽然具有相同的初始偏心距，但由于长细比不同，其承受纵向力N的能力明显不同，N₀>N₁>N₂，即由于长细比的加大，降低了构件的承载力。

我国原《规范》（GB50010—2002）中，采用把初始偏心距e_i值乘以一个偏心距增大系数_η解决纵向弯曲影响问题，即：

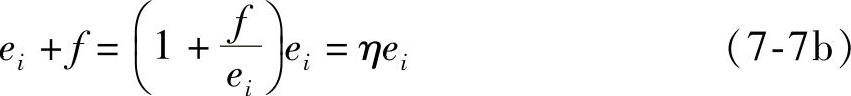
式中 f——由纵向弯曲所产生的侧向最大挠度值；

η——偏心距增大系数；

e_i——初始偏心距。

η值可近似推导如下：

试验表明，对于两端铰接柱的侧向挠度曲线近似符合正弦曲线（图7-17），即

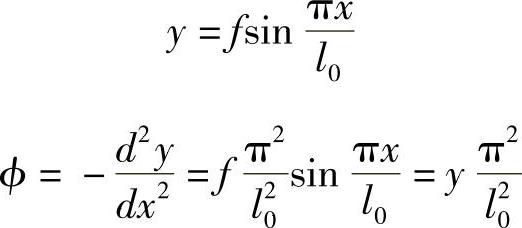
则可近似认为：

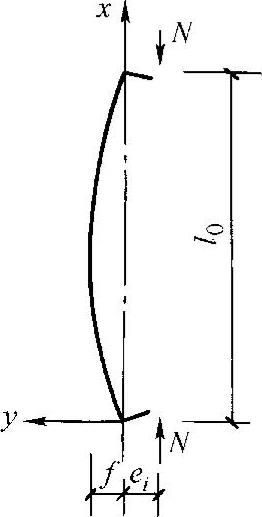
图7-17 柱的挠度曲线

根据平截面假定，可求得

对于界限破坏情况，混凝土受压区边缘应变值ε_c=ε_cu=0.0033×1.25（其中1.25是考虑柱在长期荷载作用下，混凝土徐变引起的应变增大系数，该系数值是参照国外规范确定的经验系数），钢筋应变值ε_s=ε_y=f_y/E_s（近似取f_y/E_s=0.0017）。这样，界限破坏时的曲率ϕ_b为

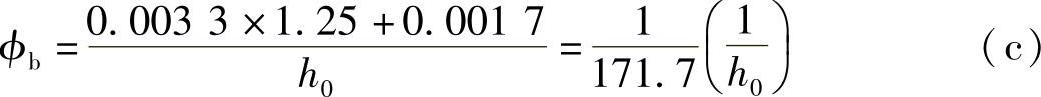
破坏时，最大曲率在柱中点，可求得界限破坏时柱中点最大侧向挠度值f为

对于“受压破坏”的偏心受压构件，离纵向力较远一侧钢筋可能受拉或受压但不屈服，且受压区边缘混凝土的应变值ε_c一般也小于0.0033，截面破坏时的曲率小于界限破坏时的曲率ϕ_b值。为此，在计算破坏曲率时，需引进一个截面曲率修正系数ζ₁值，参考国外规范和试验结果，可采用下列表达式：

式中 N——纵向力设计值；

N_b——在x=x_b时的构件界限受压承载力；《规范》近似取N_b=0.5f_cA；

A——构件截面面积；对T形、I形截面均取A=bh+2（b′_f-b）h′_f；

f_c——混凝土轴心抗压强度设计值。

对于“受拉破坏”的偏心受压构件，截面破坏时的曲率大于界限曲率ϕ_b值，但受拉钢筋屈服时的曲率则小于ϕ_b值，而破坏弯矩和受拉钢筋屈服时能承受的弯矩值很接近。为此，计算曲率可以视为和界限曲率相等。《规范》中规定，用式（7-8）求得ζ₁>1时，可取ζ₁=1。

试验还证明，随着长细比的增大，达到最大承载力时的截面应变值ε_c和ε_s减小，使控制截面的极限曲率随l₀/h的增加而减小；也可通过乘一个修正系数ζ₂值来解决。《规范》规定

ζ₂为构件长细比对截面曲率的影响系数，当l₀/h<15时，取ζ₂=1.0。

综上所述，由式（7-7b）、式（d）和系数ζ₁、ζ₂，可得

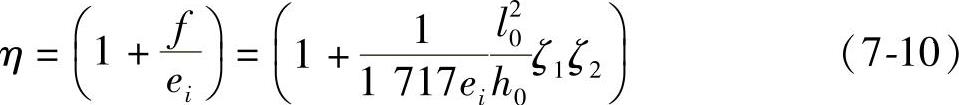
近似取h=1.1h₀，可得

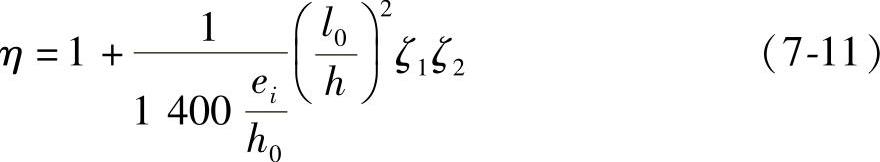
当构件长细比l₀/h（或l₀/d）≤5时，可不考虑挠度对偏心距的影响。设计时可取η=1。当环形截面时d为外直径，圆形截面时d为直径。当偏心受压构件的截面为环形或圆形时，式（7-11）中的h换成d，h₀≈0.9d。

式（7-11）不仅适合于矩形、圆形和环形，也适合于T形和I形，式（7-11）的h与h₀分别为其截面总高度和有效高度。

我国新《混凝土结构设计规范》（GB50010—2010）采用美国规范采用的方法，不再用偏心距增大系数，而改用弯矩增大系数。除排架结构柱外，其他偏心受压构件考虑轴向压力在挠曲杆件中产生的二阶效应后控制截面的弯矩设计值，应按下列公式计算：

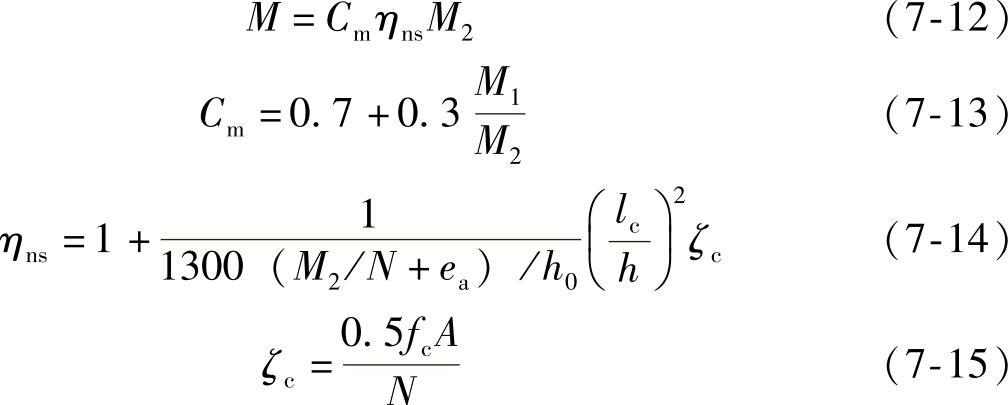
当C_mηns小于1.0时，取1.0；对剪力墙及核心筒墙，可取C_mη_ns等于1.0。

式中 C_m——构件端截面偏心距调节系数，当小于0.7时取0.7；

η_ns——弯矩增大系数；

ζ_c——截面曲率修正系数，当计算值大于1.0时，取1.0；

e_a——附加偏心距，其值应取20mm和偏心方向截面最大尺寸的1/30两者中的较大值。

η_ns使用中国习惯的极限曲率表达式。该表达式借用2002版混凝土规范偏心距增大系数_η的形式，并作了下列调整：考虑钢材强度总体有所提高，故将反映极限曲率的“1/1400”改为“1/1300”；根据对P-δ效应规律的分析，取消了2002版规范公式中在长细比偏大情况下减小构件挠曲变形的系数ζ₂。

C_m数值比美国规范略高，这是考虑到钢筋混凝土偏心压杆P-δ效应规律的离散性较大。

应注意：新规范在配筋计算前，要考虑弯矩增大系数，然后再求偏心距e₀。

为了全面理解上述公式，下面简要介绍美国规范关于二阶效应的推导和计算。

因为柱两端有无侧移，其二阶效应有很大的不同。因此，美国规范首先把柱分为无侧移柱和有侧移柱两类。图7-18为无侧移柱的二阶效应。因柱两端无侧移，故二阶效应只有P-δ效应，即纵向弯曲的影响，此时两端的附加弯矩等于零（如图7-18d）。无侧移柱的一阶最大弯矩M₂出现在柱端，最大附加弯矩出现在柱中间，此处的一阶弯矩小于或等于M₂（图7-18c，d，e）。图7-19为有侧移柱的二阶效应，它包括P-δ效应和P-Δ效应，柱两端的附加弯矩不仅不为零，并且比较大，一般考虑了二阶效应后的最大弯矩仍出现在柱端（如图7-19b，c，d）。

（1）无侧移柱 无侧移柱没有侧移，或者说其侧移可以忽略不计，因此P—Δ效应可以不考虑，而只需考虑P—δ效应，即柱的纵向弯曲的影响。

1）l₀的确定：按规范取

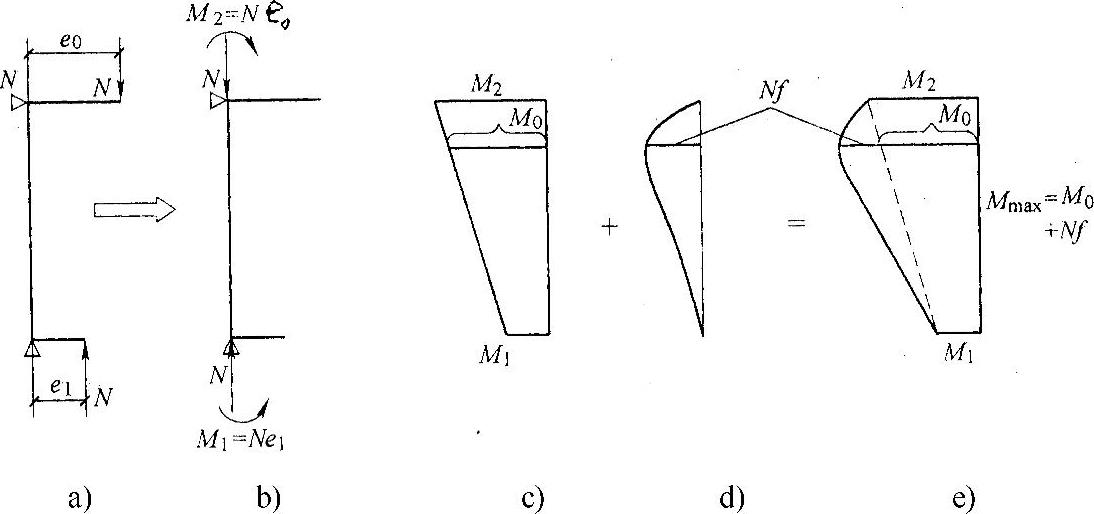
图7-18 无侧移柱的二阶效应(www.xing528.com)

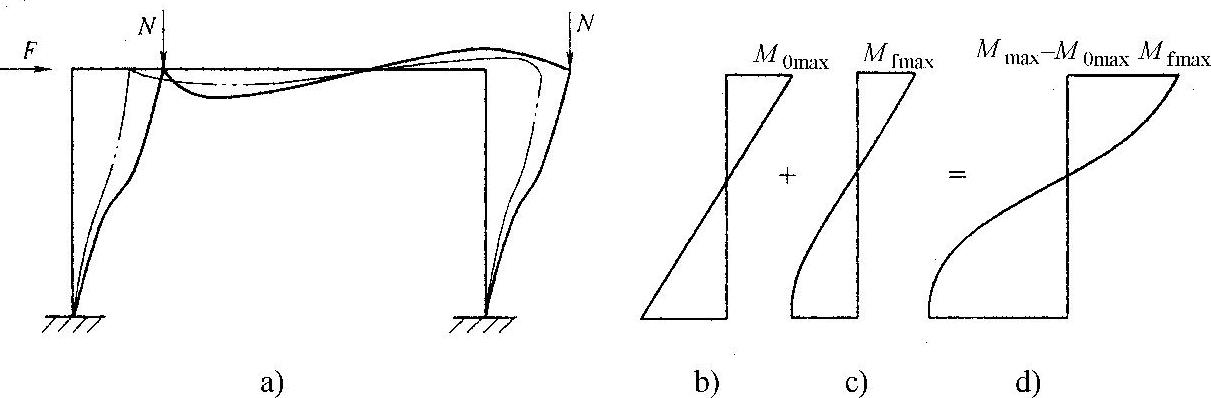
图7-19 有侧移柱的二阶效应

l₀=kl_u （a）

式中 l_u——柱的无支撑长度，即两端侧向支撑（如楼板）间的净距。

基于Furlong等的研究成果，美国规范采用以下公式计算k值：对无侧移柱取以下两式的较小值

k=0.7+0.05（ψ_A+ψ_B）≤1.0 （b）

k=0.85+0.05ψ_min≤1.0 （c）

式中，ψ_A和ψ_B分别是柱两端的柱梁相对刚度ψ

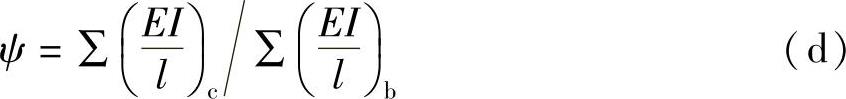
式中，分子为端点处相交各柱的线刚度之和，分母为端点处相交各梁线刚度之和。

k也可由规范中的诺模图求得。

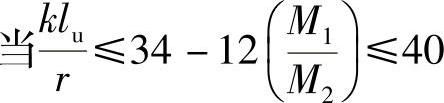时，可作为短柱处理，不需考虑二阶弯矩影响。M₂为柱端绝对值较大的弯矩，取正号；如柱单曲率弯曲，M₁为正；如双曲率弯曲，M₁为负。

2）弯矩增大系数η：规范认为无侧移柱应按轴力N_u和增大了的弯矩M_u来设计，即

M_u=ηM₂ （e）

式中，M₂是较大的端弯矩，取正号。

对于_η的计算，美国规范是基于弹性稳定理论。它以铁木辛科的公式为基础而加以适当的修正。铁木辛科的公式为

式中，N为轴力；N_cr为临界轴力

EI为截面的弹性抗弯刚度。

规范根据MacGregor、Mirza等的研究，采用如下公式

EI为考虑了截面开裂、混凝土的徐变及混凝土应力应变曲线非线性和钢筋影响的截面折算刚度，

或采用简化公式

式中，I_g为混凝土毛截面的惯性矩；I_s为钢筋对柱截面重心的惯性矩；β_d为考虑混凝土徐变的系数，等于长期荷载与总荷载的比值。

其中有几点应注意：

1）采用截面折算惯性矩：因为计算柱的临界荷载时必须考虑截面开裂、混凝土的徐变及混凝土应力应变曲线非线性和钢筋影响。

2）N_cr之前引入了系数0.75：这是一个刚度折减系数。

3）计算η公式的分子中引入系数c_m，c_m是等效弯矩修正系数。因为在发生最大附加弯矩处的一阶弯矩不是M₂，而是c_mM₂（见图7-18e和图7-20）。根据MacGregor的研究，规范采用

式中，M₁是较小的端弯矩，当柱的挠度曲线是单曲率时M₁为正，是双曲率时M₁为负。如柱两端内作用有横向荷载，c_m取为1。

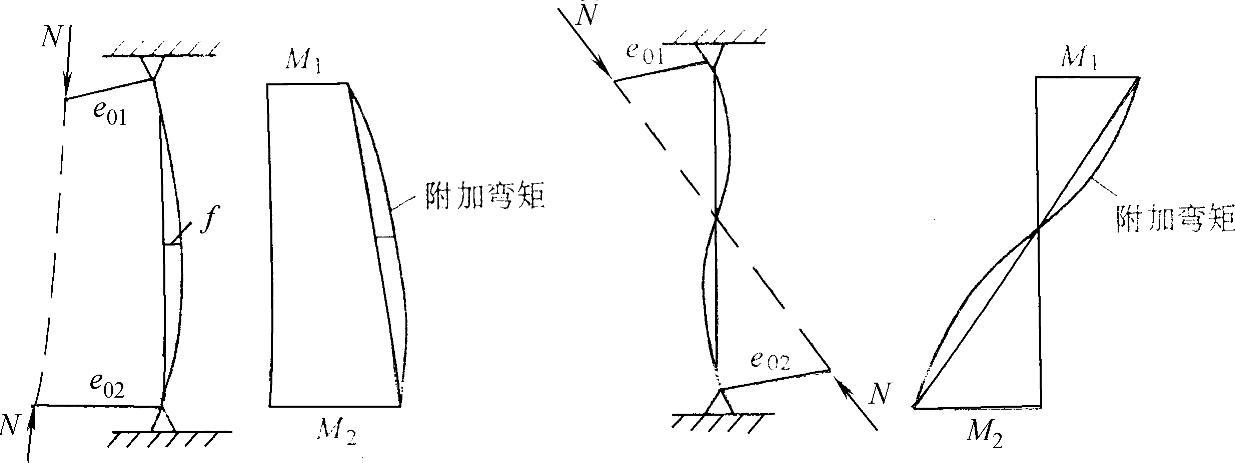
图7-20 柱端弯矩对η的影响

（2）有侧移柱 有侧移的柱因为有侧移，因此P-Δ效应和P-δ效应都应考虑，问题比较复杂。

1）l₀的确定：与无侧移柱相同，即

l₀=kl_u （m）

式中，l_u是柱的无支撑长度，即两端侧向支撑（如楼板）间的净距。对两端有约束的有侧移柱

当ψ_m<2时

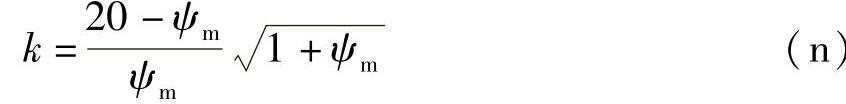
当ψ_m≥2时

对一端有约束的有侧移柱

k=2.0+0.3ψ （p）

式中，ψ_m为柱两端的柱梁平均相对刚度；ψ有约束端的柱梁相对刚度。

2）有侧移柱的设计弯矩M_u：规范认为有侧移柱应按轴力N_u和设计弯矩M_u来设计。

M_u的确定分以下三种情况。

①kl_u/r<22，此时可按短柱设计，即无需考虑二阶弯矩的影响。

②22≤kl_u/r和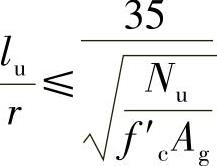，A_g为柱的毛截面积。此时有

M₁=M_1ns+δ_sM_1s （q）

M₂=M_2ns+δ_sM_2s （r）

式中，M₁和M₂为端点1和端点2处增大了的弯矩；M_1ns和M_1s分别是由不引起明显侧移的荷载（竖向荷载）和引起明显侧移的荷载（横向荷载）在柱端1产生的一阶端弯矩；M_2ns和M_2s分别是由不引起明显侧移的荷载（竖向荷载）和引起明显侧移的荷载（横向荷载）在柱端2产生的一阶端弯矩；δ_s为有侧移柱的弯矩增大系数。

注意，在这种情况下，只有M_s得到了增大，M_ns并没有增大。因为P-Δ效应只增大M_s，同时因长细比不很大，纵向弯曲效应不明显，最大弯矩出现在端点处。

设计弯矩取两者（M₁或M₂）的较大值。M₁和M₂的计算有以下三个办法：

A.采用考虑了二阶弯矩效应的弹性有限元法，构件刚度采用折算刚度。算得的弯矩M₁和M₂直接用于截面设计，这是首选的方法。

B.采用线弹性有限元法，算得一阶弯矩和侧移值，然后加以修正。在得到一阶弯矩和侧移值后，可由下式计算δ_s，然后代入式（q）和式（r），得到M₁和M₂；如算得的δ_s>1.5，则应采用A法或C法。δ_s的计算为

式中，Q为楼层稳定指数；V_u是由一阶分析得到的楼层剪力；Δ₀是与V_u相应的楼层侧移；l_c为柱的节点中到中的长度。

C.采用与式（h）类似的公式计算

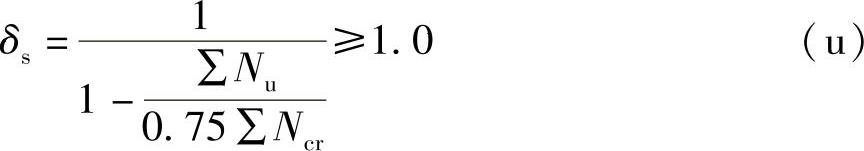
注意此式与式（h）的不同在于，在分母的计算中N_u和N_cr都是对整个楼层的柱求和，这是因为整个楼层的柱的侧移都是相同的。

③如柱的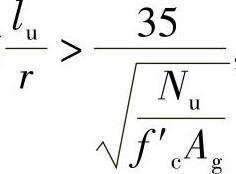，此时还必须考虑纵向弯曲的影响，即最大弯矩可能出现在两端点之间。此时需在完成了②中的计算后，再按无侧移柱的方法计算M_u，然后采用N_u和M_u进行截面设计。