弯剪扭共同作用下的承载力计算结果

图6-16为矩形截面构件弯、剪、扭内力具有不同比值和不同配筋情况下的三种典型的破坏形态。图6-16a所示的破坏形态为构件底面及两侧面的混凝土开裂后，底部钢筋首先屈服，然后顶面混凝土被压碎而破坏。这种破坏通常发生在剪力很小，弯矩与扭矩的比值较大，底部钢筋多于顶部钢筋的情况。该类破坏主要由弯矩引起，故称为弯型破坏。

图6-16b所示的破坏形态为构件顶面及两侧面的混凝土开裂后，顶部钢筋因受扭屈服后引起底部混凝土被压碎而破坏。这种破坏一般发生在剪力很小，扭矩与弯矩的比值较大，且上部纵筋较少时的情况。该类破坏主要由扭矩引起，故称为扭型破坏。

图6-16c所示的破坏形态为截面长边一侧混凝土开裂后，该侧的纵筋（抗扭）和箍筋（抗扭、抗剪）首先屈服，然后另一长边压区混凝土被压碎而破坏。这种破坏通常发生在弯矩很小，剪力和扭矩较大时的情况，故称为扭剪型破坏。如配筋合适，该类破坏形态与图6-5b类同。

由上述可知，配筋矩形截面构件在弯、剪、扭复合受力情况下的破坏形态与截面尺寸大小及高宽比值；混凝土强度大小；弯、剪、扭内力大小及相互比值；截面上、下纵筋承载力比值；纵筋与箍筋配筋强度比等因素有关。

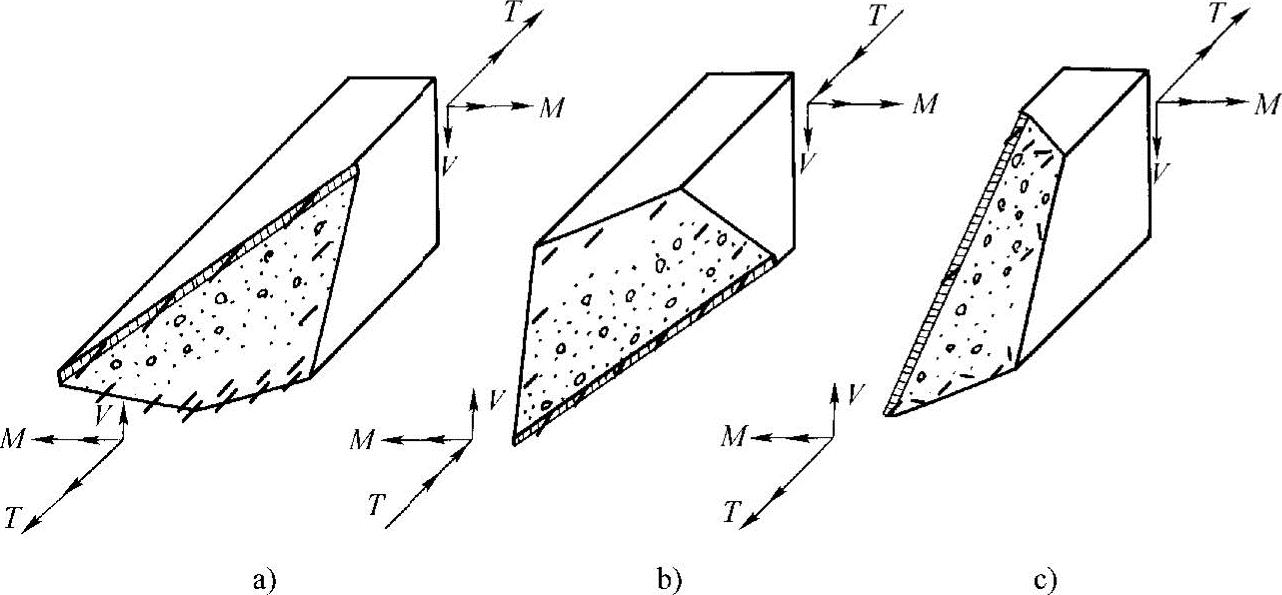
图6-16 弯剪扭构件的破坏形态及其破坏类型

a）弯型破坏 b）扭型破坏 c）扭剪型破坏

由于钢筋混凝土构件在弯矩、剪力和扭矩共同作用下的受力性能复杂，影响因素又很多。因此，目前弯、剪、扭共同作用下的矩形、T形、Ⅰ形和箱形截面的承载力计算还是采用按受弯和受剪扭分别计算，然后进行叠加的近似计算方法。即纵向钢筋应通过正截面受弯承载力和剪扭构件的受扭承载力计算求得的纵向钢筋进行配置，重叠处的纵筋截面面积可叠加。箍筋应按剪扭构件受剪承载力和受扭承载力计算求得的箍筋进行配置，相应部分处的箍筋截面面积也可叠加。

1.矩形截面弯剪扭构件的承载力计算

矩形截面弯、剪、扭构件的承载力计算可按下列规定进行。

1）当V≤0.35f_tbh₀或V≤0.875f_tbh₀/（λ+1）时，剪力对构件承载力的影响较小，可不予考虑，此时，仅按正截面受弯承载力和纯扭构件承载力分别进行纵筋和箍筋的配筋计算，并各按所需纵筋截面面积进行配置，即将抗弯纵筋与抗扭纵筋按图6-15所示叠加。

2）当T≤0.175f_tW_t或T≤0.175α_hf_tW_t时，扭矩对构件承载力的影响较小，可不予考虑，此时，仅按受弯构件的正截面受弯承载力和斜截面受剪承载力分别进行纵筋和箍筋的配筋计算。(www.xing528.com)

3）当V>0.35f_tbh₀或V>0.875f_tbh₀/（λ+1），且T>0.175f_tW_t或T>0.175α_hf_tW_t时，纵向钢筋应按受弯构件的正截面受弯承载力和剪扭构件的受扭承载力分别按所需的钢筋截面面积进行配置，即将抗弯纵筋与抗扭纵筋叠加，配置在相应的位置；箍筋应按剪扭构件的受剪承载力和受扭承载力分别按所需的箍筋截面面积进行配置，即按剪扭构件的受剪承载力和受扭承载力分别计算箍筋量，然后叠加，配置在相应的位置。钢筋的布置要满足相应的构造要求，在重合部位处的纵筋或箍筋截面面积可先叠加，再选配钢筋。

剪扭构件的受扭承载力应按式（6-38）或式（6-41）计算；剪扭构件的受剪承载力应按式（6-37）或式（6-39）或式（6-40）或式（6-42）计算。

分析表明，按上述叠加配筋方法，弯剪扭构件的受弯承载力、受剪承载力与受扭承载力之间具有相关关系，且与试验的结果大致相同。

2.T形和Ⅰ形截面弯剪扭构件的承载力计算

仍按矩形截面弯剪扭构件的规定进行，但应注意以下几点：

（1）按T形截面受弯构件进行正截面受弯承载力计算。

（2）进行截面划分和扭矩分配；腹板按剪扭构件进行承载力计算；翼缘按纯扭构件进行承载力计算。

（3）腹板的受剪承载力应按式（6-37）或式（6-39）计算，计算β_t时应将T及W_t分别以T_w及W_tw代替。

（4）腹板的受扭承载力应按式（6-38）计算，计算时应将T及W_t分别以T_w及W_tw代替；翼缘的受扭承载力应按式（6-23）计算，计算时应将T及W_t分别以T′_f及W′_tf或T_f及W_tf代替；翼缘中配置的箍筋应贯穿整个翼缘。

箱形截面弯剪扭构件的承载力计算同上，但剪扭承载力计算采用式（6-40）～式（6-44）。