开裂扭矩研究，应用于矩形截面纯受扭构件

试验表明，构件开裂前抗扭钢筋的应力很低，钢筋的存在对开裂扭矩的影响很小，因此，在研究开裂扭矩时，可以忽略钢筋的存在。

由材料力学可知，对于匀质弹性材料，矩形截面构件在扭矩T的作用下产生自由扭转时，截面将产生剪应力τ（图6-2a）。截面剪应力分布如图6-2b所示，最大剪应力发生在截面长边中点。由微元平衡条件可知，截面的主拉应力σ_tp=τ，其方向与构件轴线成45°角（图6-2a）。由试验可知，混凝土的抗拉强度低于其抗剪强度，当主拉应力超过混凝土的抗拉强度时，混凝土将首先在截面长边中点处，垂直于主拉应力方向上开裂。所以在纯扭构件中构件裂缝与纵轴线呈45°夹角。

对于理想弹塑性材料来说，截面上某一点的应力达到强度极限时并不立即破坏，该点能保持极限应力不变而继续变形，整个截面仍能继续承受荷载，直到截面上各点的应力全部达到强度极限时，构件才达到极限抗扭能力。这时截面上的应力分布如图6-2c所示。

混凝土是弹塑性材料，既非完全弹性又非理想塑性，因而，受扭时的极限应力分布将介于上述两种情况之间。与实验所测得的开裂扭矩相比，按弹性应力分布计算所得的开裂扭矩值偏低，而按理想塑性应力分布计算所得的抵抗扭矩又偏高，要确切地确定真实的应力分布是十分困难的。比较切实可行的办法是在按塑性应力分布计算的基础上乘一个折减系数。

现按图6-2c所示的应力分布求其抵抗扭矩。设矩形截面的长边为h，短边为b，相应的剪应力τ=f_t。为便于计算，将截面分为四部分，两个三角形和两个梯形，如图6-2d。三角形部分的剪应力合力为

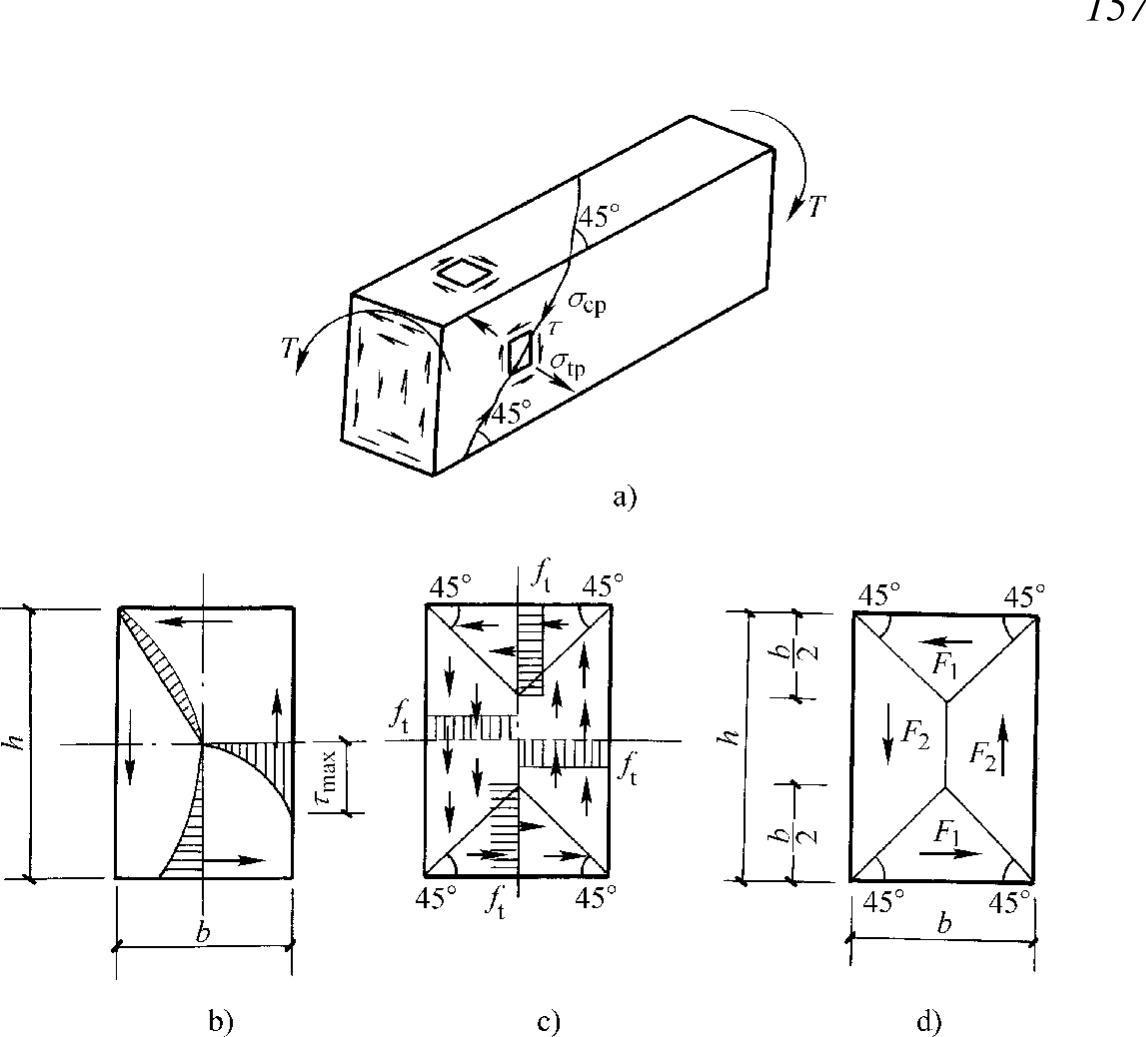
图 6-2

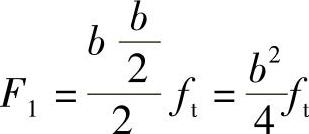
F₁到截面中心的距离为

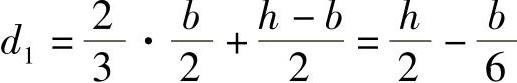
梯形部分的剪应力合力为

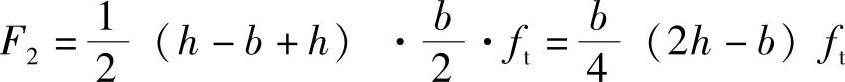(www.xing528.com)

F₂到截面中心的距离为

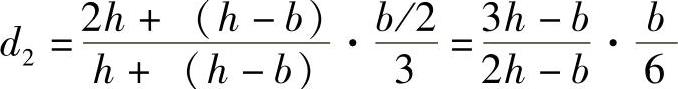
对截面中心取矩，可得抵抗矩为

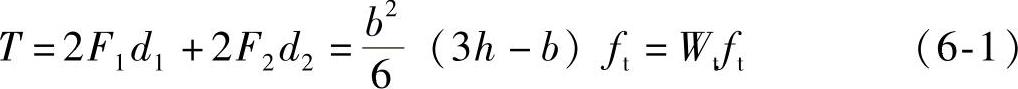
其中W_t称为矩形截面的抗扭塑性抵抗矩：

考虑到混凝土材料并非理想塑性，同时考虑到受扭构件中除了主拉应力外还有主压应力（它与主拉应力正交），混凝土在拉压复合应力状态下的抗拉强度要低于单向抗拉强度。解决这一问题的实用方法是，将上式中的f_t乘一个降低系数，取为0.7f_t，于是，开裂扭矩的计算公式为

T_cr=0.7W_tf_t （6-3）

式中W_t按式（6-2）计算。当荷载产生的扭矩

T≤T_cr=0.7W_tf_t （6-4）

时，可以认为混凝土足以承受主拉应力，抗扭钢筋可不必计算而按构造要求设置。