抵抗弯矩图及与设计弯矩图的关系

下面以一简支梁为例来说明，在进行正截面承载力计算时，首先求出设计弯矩M，然后根据承载力计算的基本公式进行配筋计算，求出A_s。抵抗弯矩图就是根据梁各截面的实际配筋情况所绘制的正截面抵抗弯矩图。抵抗弯矩图和设计弯矩图（对于连续结构则应是弯矩包络图）的关系是抵抗弯矩图必须包住设计弯矩M图，否则将不能满足正截面承载力的要求。

1.配通长直筋在抵抗弯矩图上的表示方法

一承受均布荷载的简支梁，M图如图5-22所示。梁实际配筋为1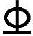18+220，当通长布置钢筋时，抵抗弯矩图如图5-22中cd段所示，即为一平直线。每根钢筋所承担的份额按各自的面积分配。因为

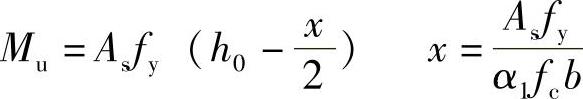
所以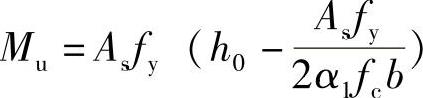

严格地讲，承载力M_u与A_s的关系并不成正比而是抛物线关系，但是在作抵抗弯矩图时，可近似假定为成正比关系。

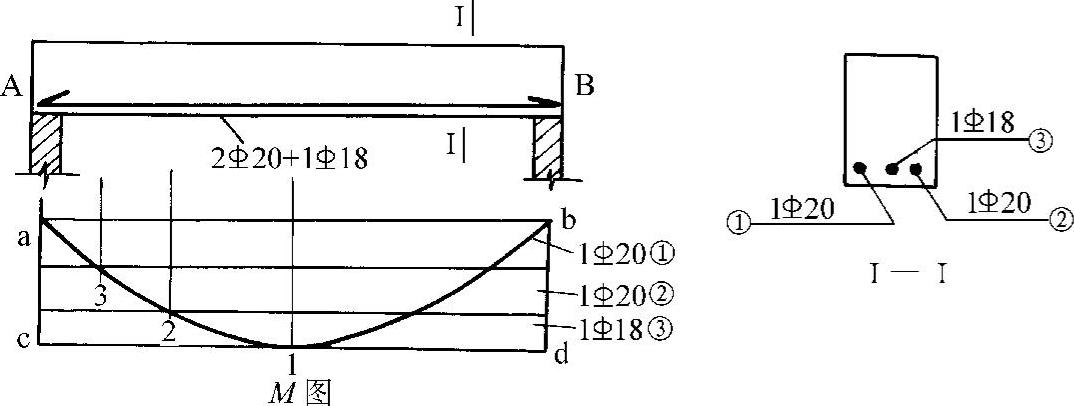
图5-22 配通长直筋简支梁的材料抵抗弯矩图

抵抗弯矩图cd与M图相切的1点是全部钢筋即①、②、③号钢筋的充分利用点；2点是③号钢筋的理论切断点，也是①、②号钢筋的充分利用点。因此，理论切断点和充分利用点具有相对性，同一点可以有两种称谓，但必须指明是相对于哪些钢筋。

2.弯起钢筋在抵抗弯矩图上的表示方法及保证斜截面抗弯的构造措施

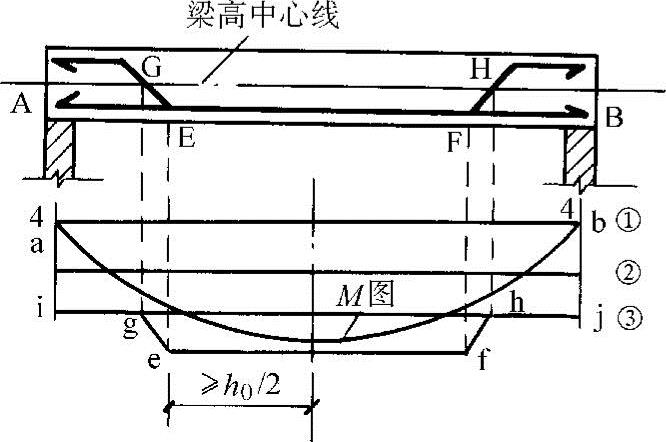
图5-23 配弯起钢筋简支梁的材料抵抗弯矩图

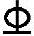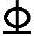（1）弯起钢筋在抵抗弯矩图上的表示方法 如图5-23所示跨中钢筋为118+220，可将中间一根钢筋即③号钢筋118弯起。钢筋弯起后，自起弯点开始正截面抗弯能力逐渐降低，直至G点（梁高中心点）弯起钢筋不再承受弯矩。此时，弯矩由2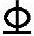20承担。弯起钢筋的抵抗弯矩图用斜直线eg和fh表示。图5-23表示了配弯起钢筋简支梁的材料抵抗弯矩图。从E至F钢筋数量不变（118+2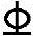20），因此抵抗弯矩图为直线ef，1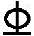18分别自E点和F点弯起，故正截面抗弯能力逐渐降低，至G点和H点就不再承担弯矩，抵抗弯矩图用斜线eg和fh表示。从G至A或从H至B抵抗弯矩由2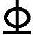20承担，即为水平直线ig和hj。全梁的抵抗弯矩图为igefhj。

（2）为保证斜截面抗弯承载力纵筋弯起时的构造要求 如图5-24所示，a为弯起钢筋起弯点至该钢筋充分利用点之间的距离。

Ⅰ-Ⅰ正截面抗弯承载力：

M_Ⅰ-Ⅰ=Asf_yZ(www.xing528.com)

Ⅱ-Ⅱ斜截面抗弯承载力：

M_Ⅱ-Ⅱ=Asbfy^Zb+（A_s-A_sb）f_yZ

为保证斜截面的抗弯承载力不小于正截面承载力，应满足：

M_Ⅱ-Ⅱ≥M_Ⅰ-Ⅰ

即 A_sbf_yZ_b+（A_s-A_sb）f_yZ≥A_sf_yZ

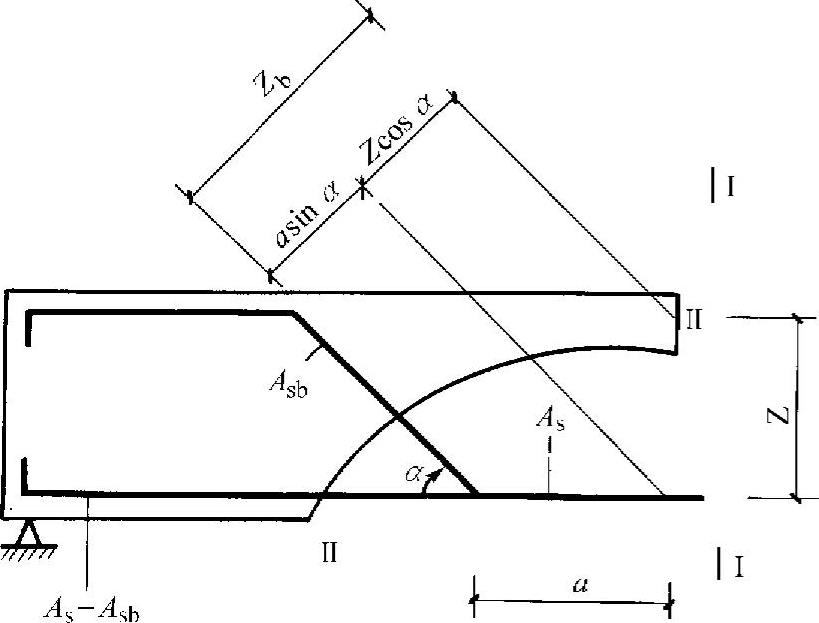
图5-24 弯起点位置

需 Z_b≥Z

根据几何关系 Z_b=asinα+Zcosα

asinα+Zcosα≥Z

所以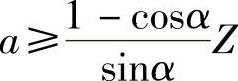

通常取α=45°或60°；Z=0.9h0

所以 a=（0.37-0.52）h₀

《规范》取a≥0.5h₀

为保证斜截面抗弯承载力要求，弯起钢筋的起弯点至该钢筋的充分利用点之间的距离a应大于等于h₀/2。