单筋矩形截面配筋设计，钢筋混凝土结构

根据式（4-6）、式（4-7）或式（4-8）就可进行截面配筋设计。为了设计方便，式（4-7）、式（4-8）可写成：

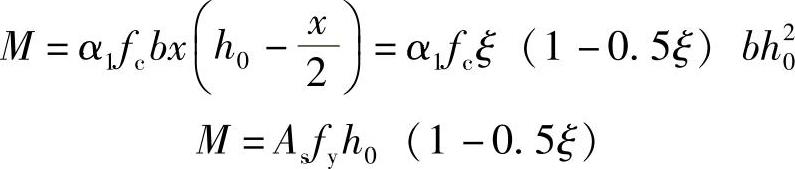
令 α_s=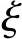（1-0.5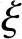） （4-9）

γ_s=1-0.5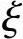 （4-10）

则 M=α₁α_sf_cbh²₀ （4-11）

或 M=A_sf_yγ_sh₀ （4-12）

截面配筋设计时经常遇到以下两种情况：

1.已知M、b、h、f_c、f_y、…，求A_s

解：（1）计算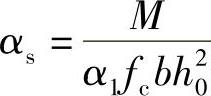

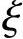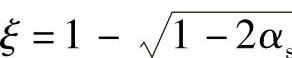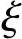（2）计算：由式（4-9）可得应不大于b

（3）计算配筋率ρ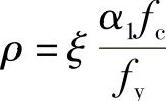，应满足ρ_min≤ρ≤ρ_b

（4）计算A_s

A_s=ρbh₀

（5）绘制配筋图。

设计时应尽量使受弯构件的配筋率落在经济配筋率范围之内，如按（3）计算的ρ值与经济配筋率相差较大也可重新选择b、h重复（1）～（4）。

2.已知M、b、f_c、f_y、…，求A_s

解：（1）先假定ρ，使ρ落在经济配筋率范围之内。

（2）根据配筋率ρ与的关系求

（3）计算α_s

α_s=（1-0.5）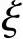

（4）由式（4-11）求h0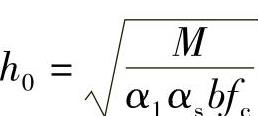

（5）计算h

h=h₀+a

计算出的h取整后（应符合建筑模数），变为已知b、h求A_s的情况。当有实际工程设计经验时，当实际取的h值大于由（5）计算的h值时也可不必重新计算而直接取A_s=ρbh₀。

【例4-1】 一矩形截面简支梁b×h=200mm×500mm，计算跨度l=6m，承受均布活荷载标准值q_k=12kN/m，均布恒荷载标准值g_k=10kN/m（不含自重），结构安全等级为二级，设计使用年限50年，按可变荷载控制的效应设计，试进行截面配筋设计。(www.xing528.com)

【解】 选C30级混凝土，f_c=14.3MPa；HRB400级钢筋，f_y=360MPa。结构安全等级为Ⅱ级γ₀=1.0。恒载分项系数γ_G=1.2；活荷载分项系数γ_Q=1.4；γ_L=1.0。

梁自重标准值g_k′=25×0.2×0.5×1kN/m=2.5kN/m（钢筋混凝土自重取25kN/m³）

简支梁跨中弯矩设计值

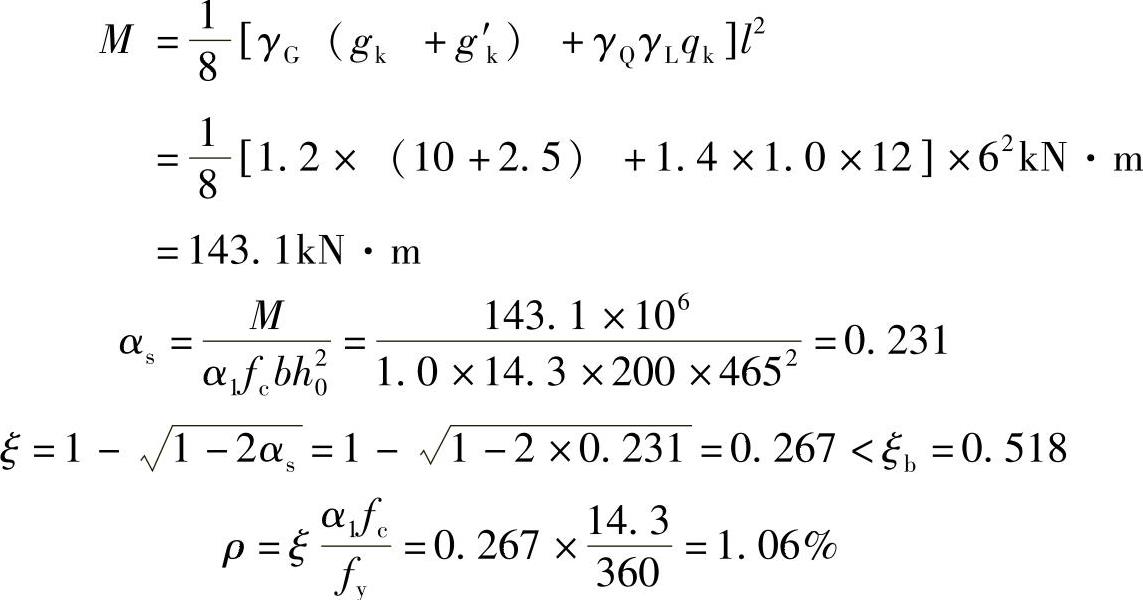
A_s=ρbh₀=1.06%×200×465mm²=985.8mm²，实配2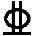22，1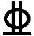18。A_s=760+254.5=1014.5mm²，如图4-14所示。

【例4-2】 一矩形截面简支梁承受弯矩设计值M=200kN·m，采用C30级混凝土，f_c=14.3MPa，HRB400级钢筋，f_y=360MPa，试确定截面尺寸及配筋。

图4-14 配筋图

【解】 选b=250mm，假设ρ=1%

则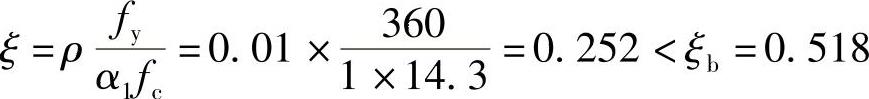

h=h₀+a=（504+35）mm=539mm

实取h=550mm。

因实际所取梁高与设计所取梁高相差较大，故应按已知b、h的情况求A_s。

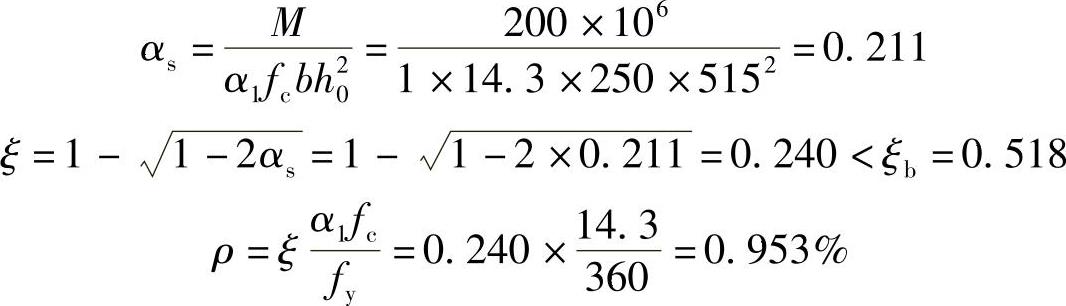
A_s=ρbh₀=0.953%×250×515=1227.0mm²，实配225，118，A_s=982+254.5=1236.5mm²。

【例4-3】 已知一安全等级为2级，设计使用年限为50年的单跨简支板，板厚120mm，板上有30mm厚水泥砂浆找平层，板的计算跨度为4.2m，板上活荷载标准值q_k=2kN/m²，混凝土采用C30级，钢筋采用HPB300，按可变荷载控制的效应设计，试进行截面配筋。

【解】 取板宽b=1000mm的板条作为计算单元。安全等级二级，γ₀=1.0；设计使用年限50年，γ_L=1.0。

恒载分项系数γ_G=1.2；活载分项系数γ_Q=1.4。

恒载标准值g_k=（1×1×0.12×25+1×1×0.03×20）kN/m=3.6kN/m。

（钢筋混凝土自重取25kN/m³，砂浆自重取20kN/m³）设计弯矩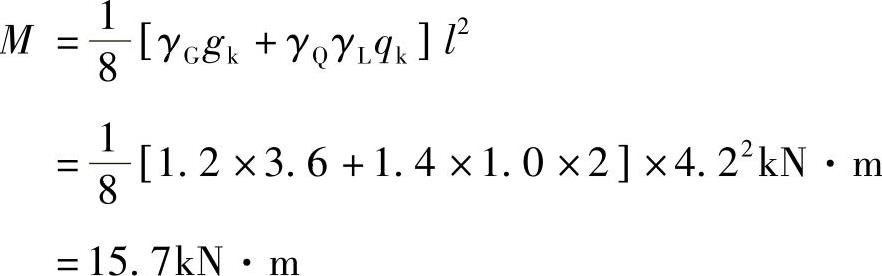

A_s=ρbh₀=0.006×1000×100mm²=600mm²，实配8/10@100，A_s=252+393=645mm²。构造筋8@200，如图4-15所示。

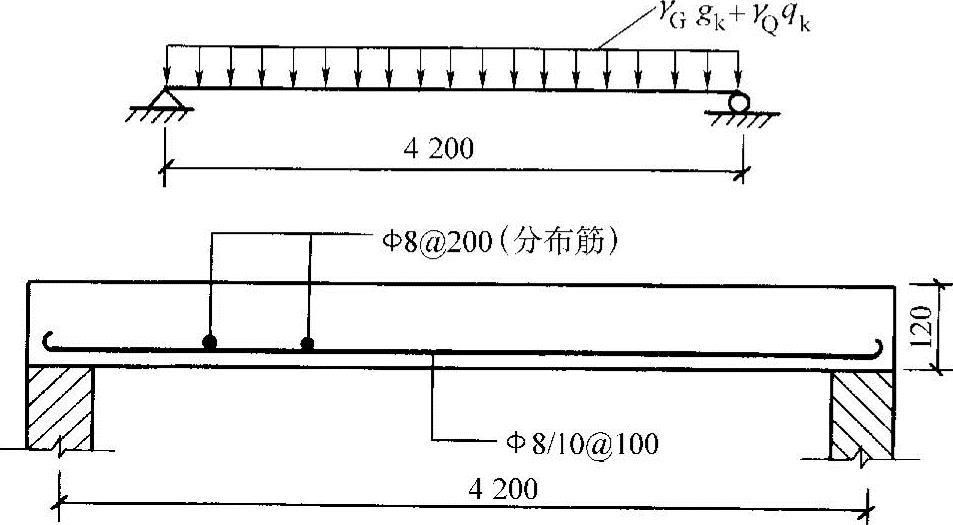
图4-15 简支板配筋图