【摘要】:适筋梁与超筋梁的分界可用两种方式表达,即ρ=ρb或=b。设界限破坏时中和轴高度为x0b,则根据平截面假定可得:图4-11 适筋梁与超筋梁、界限配筋梁破坏时的正截面平均应变图令xb为界限破坏时等效矩形应力图形上的受压区高度。
适筋梁与超筋梁的分界可用两种方式表达,即ρ=ρb或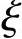 =
=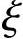 b。
b。
1.相对界限受压区高度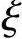 b
b
适筋梁与超筋梁的分界如图4-11中的界限破坏所示,即梁受拉筋屈服的同时受压区混凝土达到极限压应变。设钢筋屈服时的应变为εy,则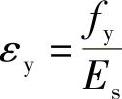 。
。
设界限破坏时中和轴高度为x0b,则根据平截面假定可得:
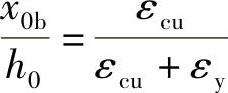
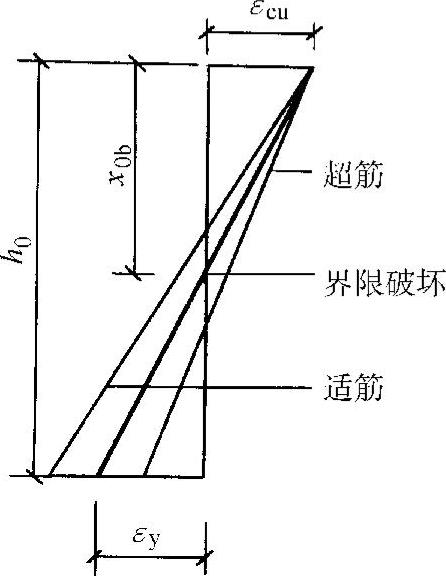
图4-11 适筋梁与超筋梁、界限配筋梁破坏时的正截面平均应变图
令xb为界限破坏时等效矩形应力图形上的受压区高度。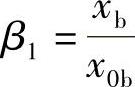 代入上式可得:
代入上式可得:
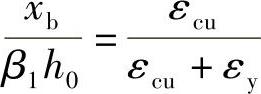
相对界限受压区高度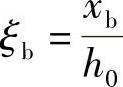 ,代入上式可得:
,代入上式可得:
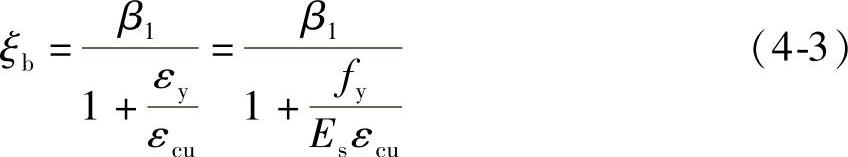
式中 fy——钢筋抗拉强度设计值;
Es——钢筋弹性模量;
εcu——非均匀受压时的混凝土极限压应变,混凝土强度等级小于等于C50时εcu=0.0033,大于C50时εcu=0.0033-(fcu,k-50)×10-5;
β1——与混凝土强度相关的系数,当混凝土强度等级小于等于C50时β1=0.8,C80时β1=0.74,其间按线性内插法确定。(https://www.xing528.com)
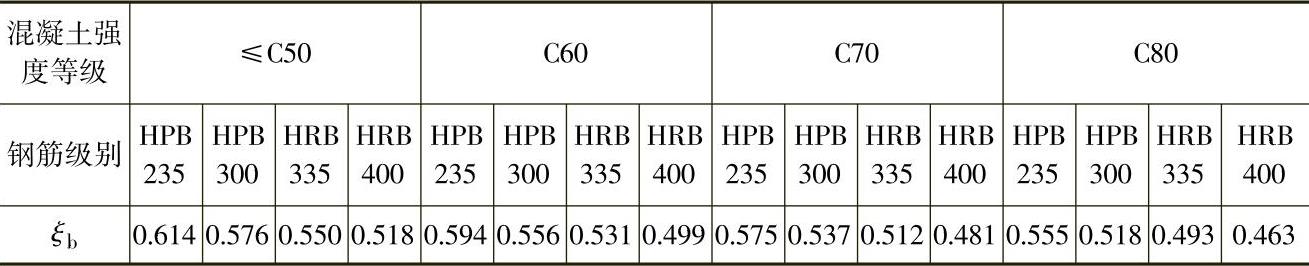
为便于设计,表4-1给出了相对界限受压区高度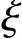 b的取值。
b的取值。
表4-1 相对界限受压区高度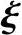 b取值
b取值
对于无明显屈服点的钢筋,钢筋的屈服应变由名义屈服应变代替(应考虑残余应变0.002的影响)即
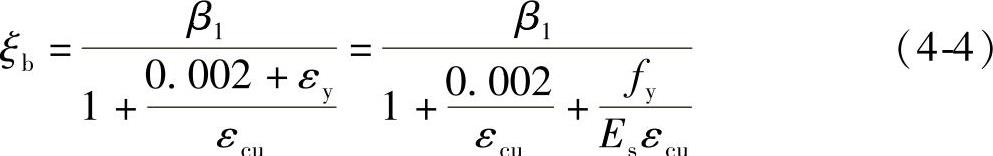
2.界限配筋率ρb
界限配筋率即为适筋梁的最大配筋率,当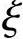 =
=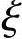 b时所对应的配筋率ρb就是界限配筋率。ρb可以由图4-12力的平衡关系得出:
b时所对应的配筋率ρb就是界限配筋率。ρb可以由图4-12力的平衡关系得出:
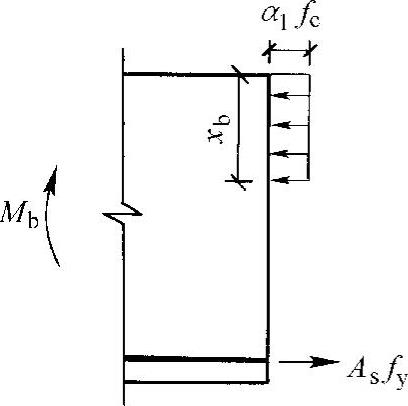
图4-12 界限破坏时的应力图形
α1fcbxb=Asfy=ρbbh0fy
所以
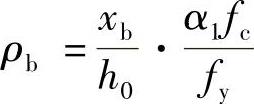

如果去掉下脚标b就可得出适筋梁配筋率ρ与相对受压区高度的关系即: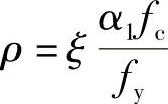 。
。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




