1.承载能力极限状态实用设计表达式
(1)一般设计表达式 由可靠指标的定义式(3-27)可得:
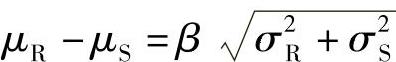
上式中等号右边的抗力项和荷载效应项是合在一起的,不便于运算。引入分离系数并使其线性化,则
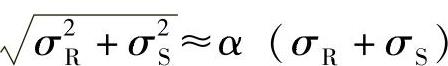
式中 α——分离系数,近似取α=0.75。
μR-μS=αβσR+αβσS=αβμRδR+αβμSδS
所以 γORμR≥γOSμS (3-32)
其中 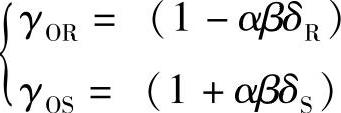
如果确定了设计可靠指标β和R、S的变异系数δR、δS,则可用式(3-32)进行设计计算。再把平均值化成标准值,就可得到混凝土结构承载能力极限状态设计表达式。对持久设计状况、短暂设计状况和地震设计状态,当用内力的形式表达时,结构构件应采用下列承载能力极限状态设计表达式:
γ0S≤R (3-33)
R=R(fc,fs,ak,……)/γRd (3-34)
式中 γ0——结构重要性系数:在持久设计状况和短暂设计状况下,对安全等级为一级的结构构件,不应小于1.1;对安全等级为二级的结构构件,不应小于1.0;对安全等级为三级的结构构件,不应小于0.9;对地震设计状况下应取1.0;
S——承载能力极限状态下作用组合的效应设计值:对持久设计状况和短暂设计状况应按作用的基本组合计算;对地震设计状况应按作用的地震组合计算;
R——结构构件的抗力设计值;
R(·)——结构构件的抗力函数;
fc、fs——混凝土和钢筋的强度设计值。
对二维、三维混凝土结构构件,当按弹性或弹塑性方法分析并以应力形式表达时,可将混凝土应力按区域等代成内力设计值,按式(3-33)进行计算;也可直接采用多轴强度准则进行设计验算。
(2)偶然作用表达式 对偶然作用下的结构进行承载能力极限状态设计时,式(3-33)中的作用效应设计值S按偶然组合计算,结构重要性系数γ0取不小于1.0的数值;式(3-34)中混凝土、钢筋的强度设计值fc、fs改用强度标准值fck、fyk(或fpyk)。
1)当进行结构防连续倒塌验算和设计时,宜符合下列要求:
①采取减小偶然作用效应的措施;
②采取使重要构件及关键传力部位避免直接遭受偶然作用的措施;
③在结构容易遭受偶然作用影响的区域增加冗余约束,布置备用的传力途径;
④增强疏散通道、避难空间等重要结构构件及关键传力部位的承载力和变形性能;
⑤配置贯通水平、竖向构件的钢筋,并与周边构件可靠地锚固;
⑥设置结构缝,控制可能发生连续倒塌的范围。
2)重要结构的防连续倒塌设计可采用下列方法:
①局部加强法:提高可能遭受偶然作用而发生局部破坏的竖向重要构件和关键传力部位的安全储备,也可直接考虑偶然作用进行设计。
②拉结构件法:在结构局部竖向构件失效的条件下,可根据具体情况分别按梁-拉结模型、悬索-拉结模型和悬臂-拉结模型进行承载力验算,维持结构的整体稳固性。
③拆除构件法:按一定规则拆除结构的主要受力构件,验算剩余结构体系的极限承载力;也可采用倒塌全过程分析进行设计。
3)当进行偶然作用下结构防连续倒塌的验算时,作用宜考虑结构相应部位倒塌冲击引起的动力系数。在抗力函数的计算中,混凝土强度取强度标准值fck;普通钢筋强度取极限强度标准值fstk,预应力筋强度取极限强度标准值fptk并考虑锚具的影响。宜考虑偶然作用下结构倒塌对结构几何参数的影响。必要时尚应考虑材料性能在动力作用下的强化和脆性,并取相应的强度特征值。
(3)既有结构的设计。
1)既有结构延长使用年限、改变用途、改建、扩建或需要进行加固、修复等,均应对其进行评定、验算或重新设计。
2)对既有结构进行安全性、适用性、耐久性及抗灾害能力进行评定时,应符合现行国家标准《工程结构可靠性设计统一标准》GB50153的原则要求,并应符合下列规定:
①应根据评定结果、使用要求和后续使用年限确定既有结构的设计方案;
②既有结构改变用途或延长使用年限时,承载能力极限状态验算宜符合混凝土结构规范的有关规定;
③对既有结构进行改建、扩建或加固改造而重新设计时,承载能力极限状态的计算应符合混凝土结构规范和相关标准的规定;
④既有结构的正常使用极限状态验算及构造要求宜符合混凝土结构的规定;
⑤必要时可对使用功能作相应的调整,提出限制使用的要求。
3)既有结构的设计应符合下列规定:
①应优化结构方案,保证结构的整体稳固性;
②荷载可按现行规范的规定确定,也可根据使用功能作适当的调整;
③结构既有部分混凝土、钢筋的强度设计值应根据强度的实测值确定;当材料的性能符合原设计的要求时,可按原设计的规定取值;
④设计时应考虑既有结构构件实际的几何尺寸、截面配筋、连接构造和已有缺陷的影响;当符合原设计的要求时,可按原设计的规定取值;
⑤应考虑既有结构的承载历史及施工状态的影响;对二阶段成形的叠合构件,可按混凝土规范关于叠合构件的规定进行设计。
2.荷载效应组合
荷载组合即指按极限状态设计时,为保证结构的可靠性而对同时出现的各种荷载设计值的规定。当结构上同时作用有多种可变荷载时要考虑到荷载效应的组合,即在所有能同时出现的各种荷载组合下,确定结构或构件内产生的总效应。我们把其中对结构构件产生总效应最不利的一组组合称为最不利组合,并取最不利组合进行设计。
《混凝土结构设计规范》(GB50010—2010)规定,对于承载能力极限状态,应采用荷载效应的基本组合或偶然组合进行设计。(https://www.xing528.com)
(1)基本组合 对于荷载基本组合的效应设计值Sd,应从下列荷载组合值中取用最不利的效应设计值确定。
1)由可变荷载控制的效应设计值:
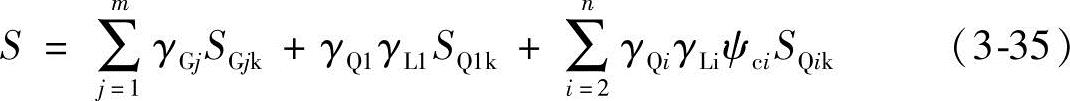
2)由永久荷载控制的效应设计值:
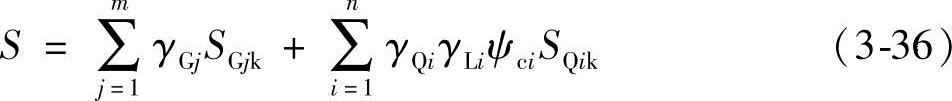
式中 γGj——第j个永久荷载的分项系数,当其效应对结构不利时,对由可变荷载效应控制的组合,应取1.2;对由永久荷载效应控制的组合,应取1.35;当其效应对结构有利时,不应大于1.0;对结构的倾覆、滑移或漂浮验算,荷载的分项系数应满足有关的建筑结构设计规范的规定;
γQi——第i个可变荷载的分项系数,其中γQ1为主导可变荷载Q1的分项系数。γQi一般情况下应取1.4;对标准值大于4kN/m2的工业房屋楼面结构的活荷载应取1.3;
SGjk——按第j个永久荷载标准值Gjk计算的荷载效应值;
SQik——按第i个可变荷载标准值Qik计算的荷载效应值,其中SQ1k为诸可变荷载效应中起控制作用者,当对SQ1k无法明显判断时,轮次以各可变荷载效应值作为SQ1k,并选取其中最不利的荷载组合效应的设计值;
γLi——第i个可变荷载考虑设计使用年限的调整系数,其中γL1为主导可变荷载Q1考虑设计使用年限的调整系数,γLi按表3-10采用;
ψci——第i个可变荷载Qi的组合值系数;
m——参与组合的永久荷载数;
n——参与组合的可变荷载数。
表3-10 楼面和屋面活荷载考虑设计使用年限的调整系数γL

应当指出,对结构构件有不同的设计状况时,则应分别按不同的状况计算荷载效应。
(2)偶然组合 荷载偶然组合的效应设计值Sd可按下列规定采用:
1)用于承载能力极限状态计算的效应设计值,应按下式进行计算:

式中 SAd——按偶然荷载标准值Ad计算的荷载效应值;
ψf1——第1个可变荷载的频遇值系数;
ψqi——第i个可变荷载的准永久值系数。
2)用于偶然事件发生后受损结构整体稳固性验算的效应设计值,应按下式进行计算:
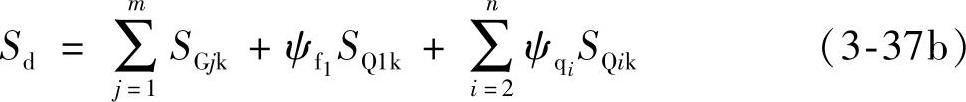
组合中的设计值仅适用于荷载与荷载效应为线性的情况。
【例3-1】 一简支梁,跨度l0=4m,受永久线均布荷载标准值qGk=8kN/m,受可变均布荷载标准值qQk=6kN/m,跨中受可变集中荷载,其标准值Pk=10kN,无风载参加组合。该梁设计使用年限为50年,且是重要的建筑构件,安全等级为一级。求该梁跨中截面的设计弯矩值。
【解】 永久荷载产生的跨中弯矩为:
由可变荷载控制的效应设计值:
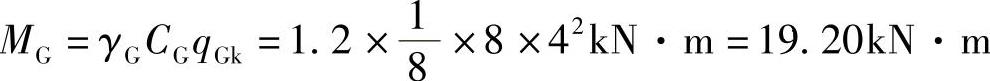
由永久荷载控制的效应设计值:
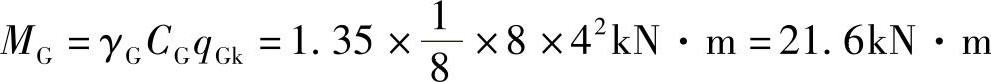
设计使用年限为50年,设计使用年限的调整系数查表3-10,得γL=1.0。
均布可变荷载产生的跨中弯矩为(按标准值大于4kN/m2的工业房屋楼面结构的活荷载考虑)
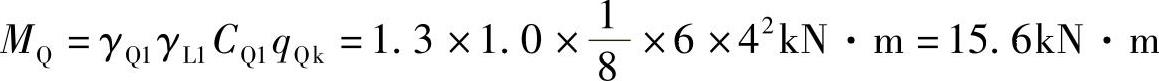
集中可变荷载产生的跨中弯矩为
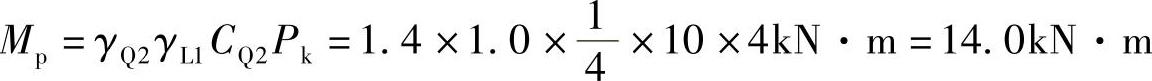
无风荷载作用,ψ=0.7。
MQ=0.7×15.6kN·m=10.92kN·m
Mp=0.7×14.0kN·m=9.8kN·m
由可变荷载效应控制的组合:
M=(19.20+15.6+9.8)kN·m=44.6kN·m
由永久荷载效应控制的组合:
M=(21.6+10.92+9.8)kN·m=42.32kN·m
安全等级为一级,取γ=1.1。于是,叠加后的最大跨中弯矩为
M=1.1×44.6kN·m=49.06kN·m
如该梁还受一地震设计状况下产生的跨中弯矩M=30kN·m。求该梁跨中截面的设计弯矩值。频遇值系数ψf1=0.6,准永久值系数ψq=0.5。
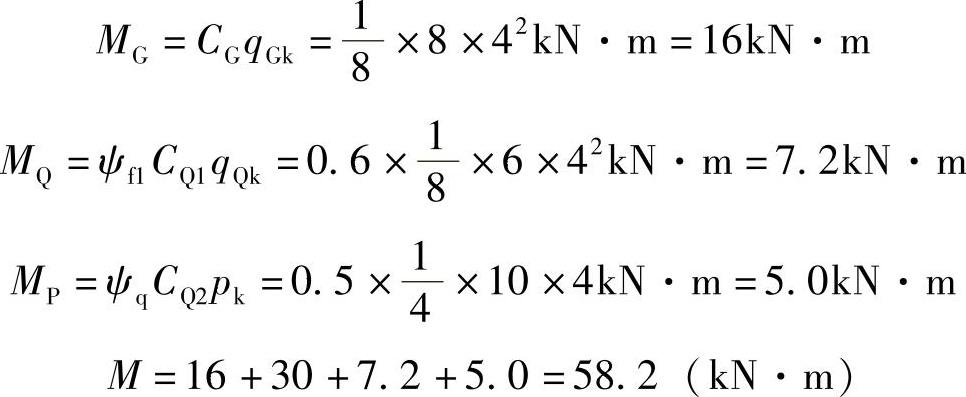
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




