钢筋混凝土结构的3.4.1可靠度和失效概率

1.可靠度

结构在规定的时间内，在规定的条件下，完成预定功能的概率，称为可靠度。

2.失效概率

失效是指结构或结构的一部分不能满足设计所规定的某一功能要求，即达到或超过了承载能力极限状态或正常使用极限状态中的某一极限。失效概率是指结构构件处于失效状态下的概率。结构能够完成预定功能（R≥S）的概率即为“可靠概率”P_s，不能完成预定功能（R<S）的概率即为“失效概率”P_f。显然，结构的可靠与失效为两个互不相容事件，因此P_s和P_f是互补的，即P_s+P_f=1.0，P_f越小，可靠度越大。

结构的极限状态是用极限状态函数（或称功能函数）来描述的。设有n个相互独立的随机变量X_i（i=1，2，…，n）影响结构的可靠度，其功能函数为

Z=g（X₁，X₂，…，X_n） （3-16）

当 Z=g（X₁，X₂，…，X_n）=0 （3-17）

时，结构已达到极限状态，式（3-17）称为极限状态方程。

若只以结构构件的荷载效应S和结构抗力R作为两个基本的随机变量来表达时，则功能函数表示为

Z=g（R，S）=R-S （3-18）

极限状态方程则为

Z=g（R，S）=R-S=0 （3-19）

因为R和S是随机变量，所以功能函数Z也是随机变量。显然，当Z>0时，结构可靠；当Z<0时，结构失效；当Z=0时，表示结构处于极限状态。

图3-3表示R与S的概率密度函数曲线，在曲线的重叠区内，如果R<S，则结构失效，其失效概率与重叠区的大小有关。当R>0，S>0时，失效概率可以写成

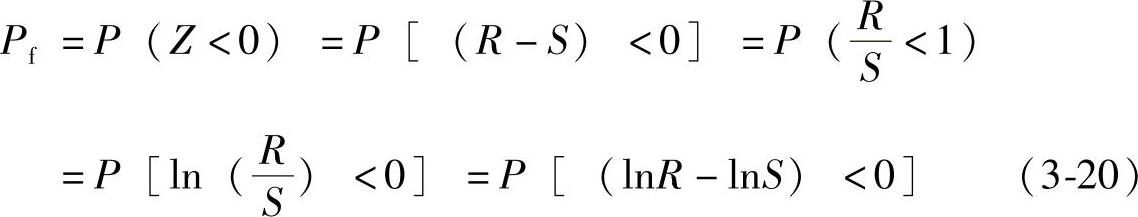
式中 P（·）——事件（·）的概率。

若F（r，s）为（R，S）的联合分布函数，f（r，s）为（R，S）的联合概率密度函数，参见图3-3，由概率论可得

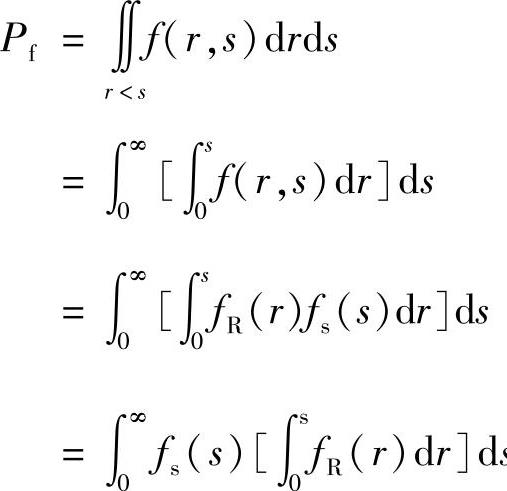
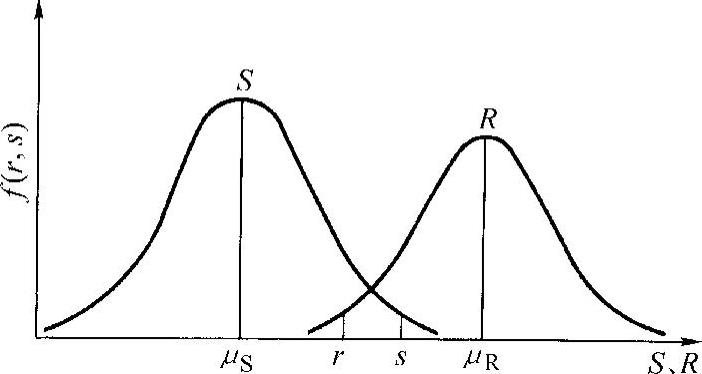
图3-3 R与S概率密度函数曲线

式中 F_R（s）=P（R<S）是假定R和S相互独立的。

式（3-21）也可以由图3-4得到解释。荷载S在s和s+ds之间的概率为f_s（s）ds，F_R（s）是R<S的概率，即F_R（s）=P（R<S）。若R和S相互独立，则此两事件同时发生的概率为其乘积F_R（s）f_s（s）ds。将此乘积在S的全域内积分即得式（3-21）。

失效概率P_f的物理意义是：对于每一个抗力的可能值，当R在r和r+dr之间时，荷载效应大于抗力的概率；或者，对于每一个荷载效应的可能值，当S在s和s+ds之间时，抗力小于荷载效应的概率。

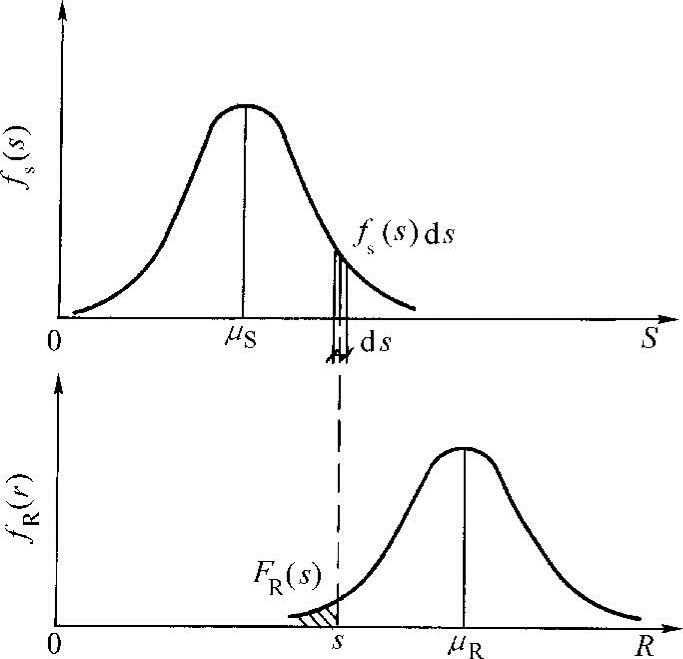
图3-4 R及S的概率分布曲线

3.可靠指标

可靠指标同样也是用以度量结构构件可靠度的指标，通常用β表示。分析表明，所有的S和R的分布中，正态分布占有一定的比例，而一些非正态分布的随机变量（如风载）可以通过数学变换转换成当量的正态分布。因此，可以认为S和R都是正态随机变量。

水准Ⅱ的近似概率计算法，在进行可靠指标计算时，分为两种方法：①不考虑随机变量的实际分布，假定它服从正态分布或者对数正态分布，导出有关的结构构件可靠指标的解析表达式，进行分析和计算。由于分析时采用了泰勒级数在平均值处（即中心点）展开，故简称为中心点法；②考虑随机变量的实际分布，将非正态分布当量正态化，并在设计验算点进行迭代，计算可靠指标，故称为验算点法。

（1）正态分布 假定抗力R和荷载效应S均服从正态分布，其平均值和标准差分别为μ_R、μ_S和σ_R、σ_S，则由概率论可知，功能函数Z=R-S也服从正态分布，Z的平均值和标准差分别为(www.xing528.com)

μ_Z=μ_R-μ_S （3-22）

图3-5表示随机变量Z的分布，Z<0的概率为失效概率，即P_f=P（Z<0），此值等于图中阴影部分的面积。图中由0到平均值_μZ这段距离，可以用标准差去度量，即

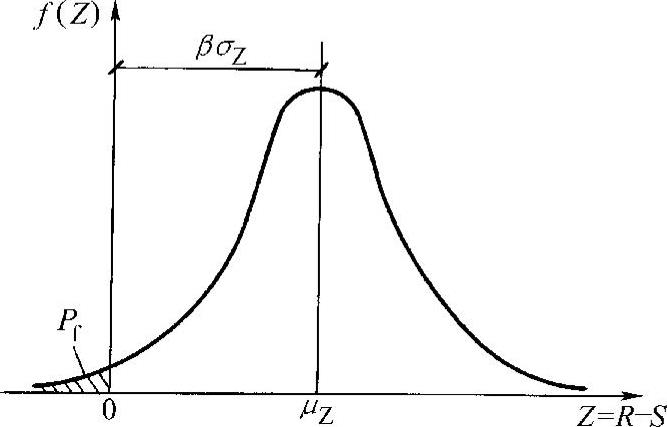
图3-5 Z=R-S的概率分布曲线及β和P_f的关系

μ_Z=βσ_Z （3-24）

不难看出，β与P_f之间存在一一对应关系，β小时，P_f就大；β大时，P_f就小。因此，β和P_f一样，也可以作为衡量结构可靠性的一个指标。

此时，失效概率为

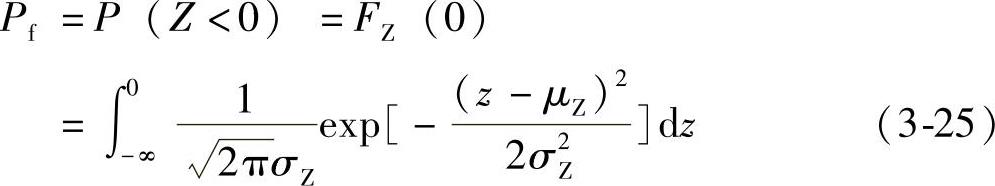
引入“标准化变量t”（即令_μt=0，σ_t=1.0）

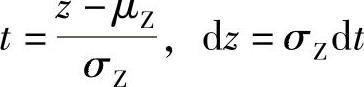
所以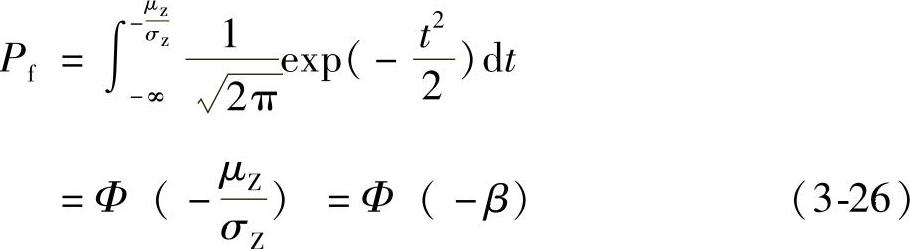

式中 Φ（·）——标准正态分布函数。

由式（3-24）、式（3-22）和式（3-23），可得可靠指标β为

由式（3-26）可知，失效概率P_f与可靠指标β之间存在一一对应关系。当R、S服从正态分布时，β与P_f的对应关系如表3-7所列。

表3-7 β与P_f的对应关系

由式（3-27）可以看出，如所设计的结构，当R和S的平均值μ_R和μ_S的差值愈大，或它们的标准差σ_R与σ_S的数值愈小，则可靠指标β值就愈大，也就是失效概率P_f愈小，结构的可靠性愈高。

（2）对数正态分布 因为抗力和荷载效应大多趋向于偏正态分布，按正态分布计算时将产生较大的误差。因此，有的学者建议可认为R和S服从对数正态分布，即R和S的对数lnR和lnS服从正态分布。lnR和lnS的平均值为μ_lnR、μ_lnS，标准差为σ_lnR、σ_lnS。此时，功能函数Z=lnR-lnS也服从正态分布，其平均值和标准差为μ_Z=μ_lnR-μ_lnS和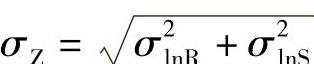。由对数正态分布的性质可知

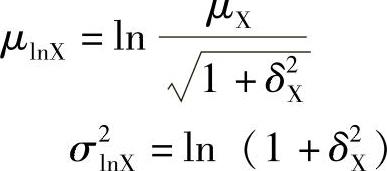
式中 δ_X——变异系数，δ_X=σ_X/μ_X。

所以

当δ_R和δ_S小于0.3时，上式可以进一步简化，取

ln（1+δ²_R）≈δ²_R，ln（1+δ²_S）≈δ²_S

其误差小于2%。且当δ_R和δ_S很小或者近似相等时，则有

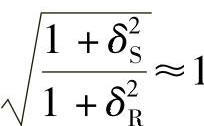
将上述结果代入式（3-28），可得简化的对数正态分布可靠指标β的计算公式为