1.混凝土的抗压强度
抗压强度是混凝土的重要力学指标，与水泥强度等级、水泥用量、水灰比、配合比、龄期、施工方法及养护条件等因素有关。试验方法及试件形状、尺寸也会影响所测得的强度数值。实验表明，相同承压面积（150mm×150mm）但外形尺寸不同的混凝土轴心受压试件，其抗压强度并不相同。图2-6a、b、c、d分别为150mm×150mm×450mm的棱柱体试件（不减摩）、150mm×150mm×150mm的立方体试件（不减摩）、150mm×150mm×150mm的立方体试件（减摩）和450mm×450mm×450mm的立方体局部承压试件。根据试验，其抗压强度（破坏荷载除以承压面积）分别为：棱柱体强度fc=15.2N/mm2（不减摩），立方体强度fcu=20N/mm2（不减摩），立方体强度fc=15.2N/mm2（减摩），局部承压强度fcl=45.6N/mm2。四个试件的破坏形态也各不相同，这主要是在单向轴心压力的作用下，混凝土产生轴向压缩应变及横向拉伸应变，而横向拉伸应变是造成纵向裂缝的主要原因。当试块与压力机垫板直接接触，无减摩措施，试块上下表面与垫板之间有摩擦力存在，使试块横向不能自由扩张，就会提高混凝土的抗压能力，此时，靠近试块上下表面的区域内，好像被箍住一样，试块中部由于摩擦力的影响较小，混凝土仍可横向鼓胀。随着压力的增加，试块中部发生纵向裂缝，然后出现通向试块角隅的斜向裂缝。棱柱体试块的高度与宽度之比h/b=3，套箍的影响只在两端局部范围内，试件中部横向变形并不受到约束，而立方体h/b=1，在很大范围内受到套箍的影响，所以棱柱体强度比立方体强度低。对局部承压试件，荷载仅作用在部分面积上，其横向变形受到未受荷载直接作用的外围混凝土的约束，所以其抗压强度最高。破坏时，中部向外鼓胀的程度也不同，如图2-6a、b所示，棱柱体试件中部基本为垂直裂缝，仅上下端成八字形裂缝，而立方体试件破坏时，中部向外鼓胀的混凝土向四周剥落，使试块只剩下一个角锥体。而局部承压试件在垫板下呈角锥形破坏，顶面垫板外的约束混凝土出现从垫板中心向外扩展的裂缝，但均未延伸到试件边缘（图2-6d）。
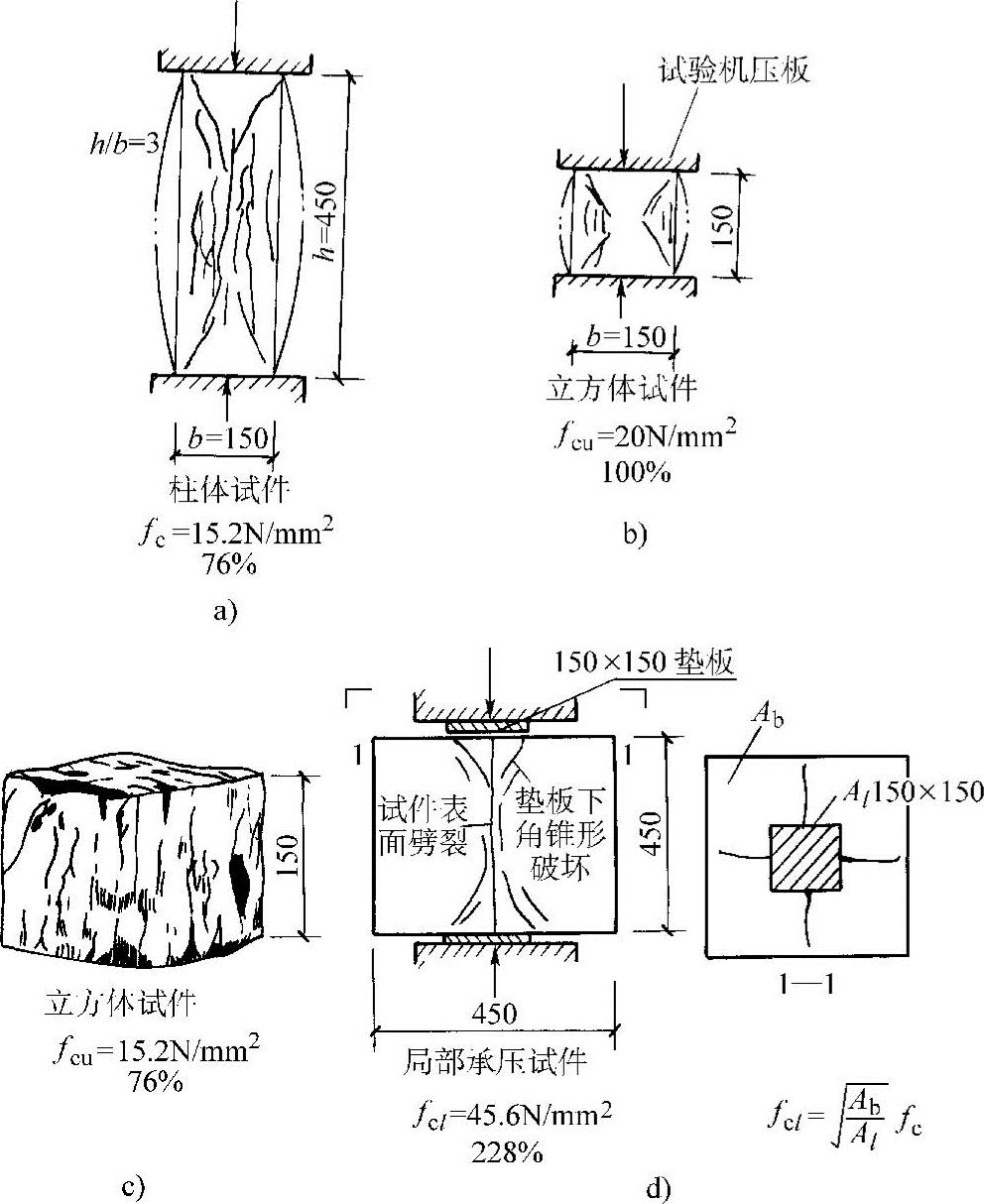
图2-6 不同外形尺寸的混凝土轴心受压试块（单位：mm）
当立方体试块上下表面涂有油脂或填以塑料薄片，以减少摩擦力时，则所测得的抗压强度就较不涂油脂者小，并与不减摩的棱柱体强度相同。破坏时，试块出现垂直裂缝，如图2-6c所示。为了统一标准，规定在试验中采用不涂油脂的试块。
由于混凝土的抗压强度是有条件的，因此，设计、施工应按不同受力情况采用不同的抗压强度作为判别标准和设计依据。
（1）标准立方体强度fcu，k 我国以150×150×150的立方体试件，在（20±3）℃的温度和相对湿度90%以上的潮湿空气中养护28d，按标准制作和试验方法（以每秒0.2～0.3N/mm2的加荷速度）测得的具有95%保证率的抗压强度[计量单位N/mm2（MPa）]作为混凝土的强度等级，也称为标准立方体强度，用fcu，k表示。如C20表示混凝土的标准立方体强度，即强度等级为20N/mm2，《混凝土结构设计规范》（GB50010—2010）共分C15～C8014个等级。它并不代表实际构件中混凝土的受力情况。但由于它的制作及试验比较简单，可作为在统一试验方法下衡量混凝土强度的相对指标。
钢筋混凝土结构的混凝土强度等级不应低于C20；采用强度等级400MPa及以上钢筋时，混凝土强度等级不应低于C25。预应力混凝土结构的混凝土强度等级不宜低于C40，且不应低于C30。承受重复荷载的钢筋混凝土构件，混凝土强度等级不应低于C30。
目前实际采用的尺寸还有200mm和100mm边长的立方体试块。试验表明。由于试验块两端摩擦的影响和尺寸效应，立方体边长越小，抗压强度越高。当边长不是150mm时，可通过尺寸效应换算系数换算成150mm的立方体试块强度（强度等级）。
强度等级=0.95×（100mm边长立方体试块强度）
强度等级=1.05×（200mm边长立方体试块强度）
由于混凝土中水泥胶块的硬化过程需要若干年才能完成，所以混凝土的强度也随龄期的增长而增长，开始增长得很快，以后逐渐变慢。试验观察得知，混凝土强度增长可延续到15年以上，保持在潮湿环境中的混凝土强度的增长会延续得更久。
混凝土不同龄期的强度应通过试验确定。当无试验资料时，在一般情况下强度随龄期的变化率可参考表2-1选用。
表2-1 混凝土抗压强度随龄期的相对变化率
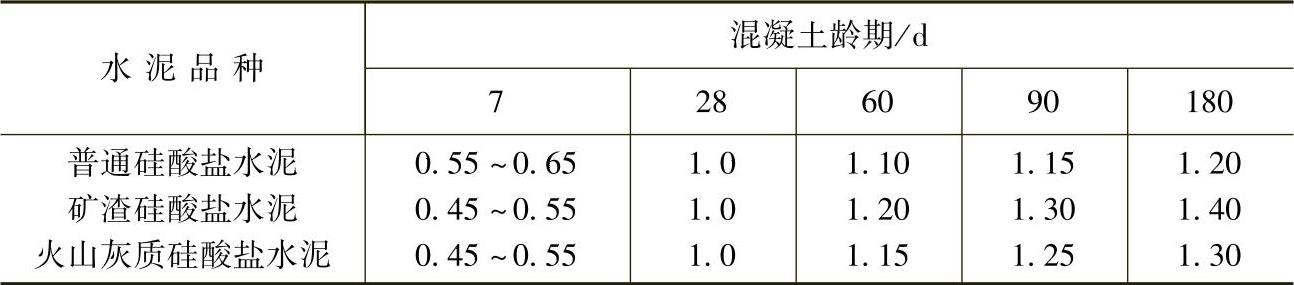
注：1.对于蒸汽养护的构件不考虑抗压强度随龄期的增长；
2.表中数字未计入掺合料及外加剂的影响；
3.表中数字适用于C30及其以下的混凝土。
（2）棱柱体抗压强度—轴心抗压强度fc（图2-6a） 若试件为棱柱体，则所测得的抗压强度称为棱柱体抗压强度fc。棱柱体试件的抗压强度比较接近实际构件中混凝土的受力情况。试验证实，轴心受压混凝土柱中的混凝土强度基本上和棱柱体抗压强度fc相同。试验还表明，fc随试件高度与宽度之比h/b而异，当h/b>3时趋于稳定。所以，一般规定用h/b=3～4的棱柱体抗压强度来代表混凝土单向均匀受压时的抗压强度。但由于宽高比为1∶2与1∶3的试件测得的强度数值相差不多，为照顾我国目前试验机的实际尺寸，所以把尺寸为150×150×300的试件定为标准试件。当试件截面尺寸相同时，国内外试验都指出，fck与fcu，k大致成线性关系，棱柱体抗压强度标准值fck和立方体抗压强度标准值fcu，k的关系为
fck=0.88αc1αc2fcu，k （2-2）
因设计需考虑实际结构构件与试件制作和养护条件的差异、尺寸效应及加荷速度等因素的影响，故规范综合考虑上述因素，并参考其他国家的有关规定，对试件混凝土强度修正系数取为0.88。
式中 αc1——棱柱体强度与立方体强度的比值，根据试验结果，并考虑到抗压强度标准值的最终结果，对C50及以下的混凝土取αc1=0.76；对C80取αc1=0.82。中间按线性插值取值。
αc2——混凝土脆性折减系数，考虑到混凝土强度越高，混凝土脆性越明显，对C40及以下的混凝土取αc2=1.0，对C80取αc2=0.87，中间按线性插值取值。脆性折减系数的定量，主要是从结构安全度上综合考虑的结果。
（3）局部承压强度fcl 凡是荷载仅作用在构件部分面积上的受力状况都可视为局部承压。例如，实际工程中屋盖大梁，桁架对柱子的荷载（图2-7a），后张法预应力混凝土构件端部锚头下的挤压力（图2-7b），偏心受压构件的混凝土受压区（图2-7c及图2-7d）等情况都属于局部承压。试验表明，局部承压强度fcl与棱柱体均匀受压强度fc的关系为
fcl=βcβlfc （2-3）
式中 βc——混凝土强度影响系数，当混凝土强度等级不超过C50时，取βc=1；当混凝土强度等级为C80时，取βc=0.8；其间按线性内插法确定；
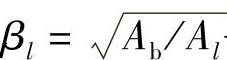——混凝土受压时的强度提高系数；
Al——混凝土局部受压面积；
Ab——局部受压的计算底面积，对于图2-7a、b所示Al四面有外围混凝土的情况，Ab可按同心（形心重合）、对称、有效面积的原则确定；对于图2-7c、d、e所示Al位于截面边、角的情况，规范从偏于安全的角度考虑，规定Ab=Al，即βl=1，不予提高，Ab的取值见图2-7f。
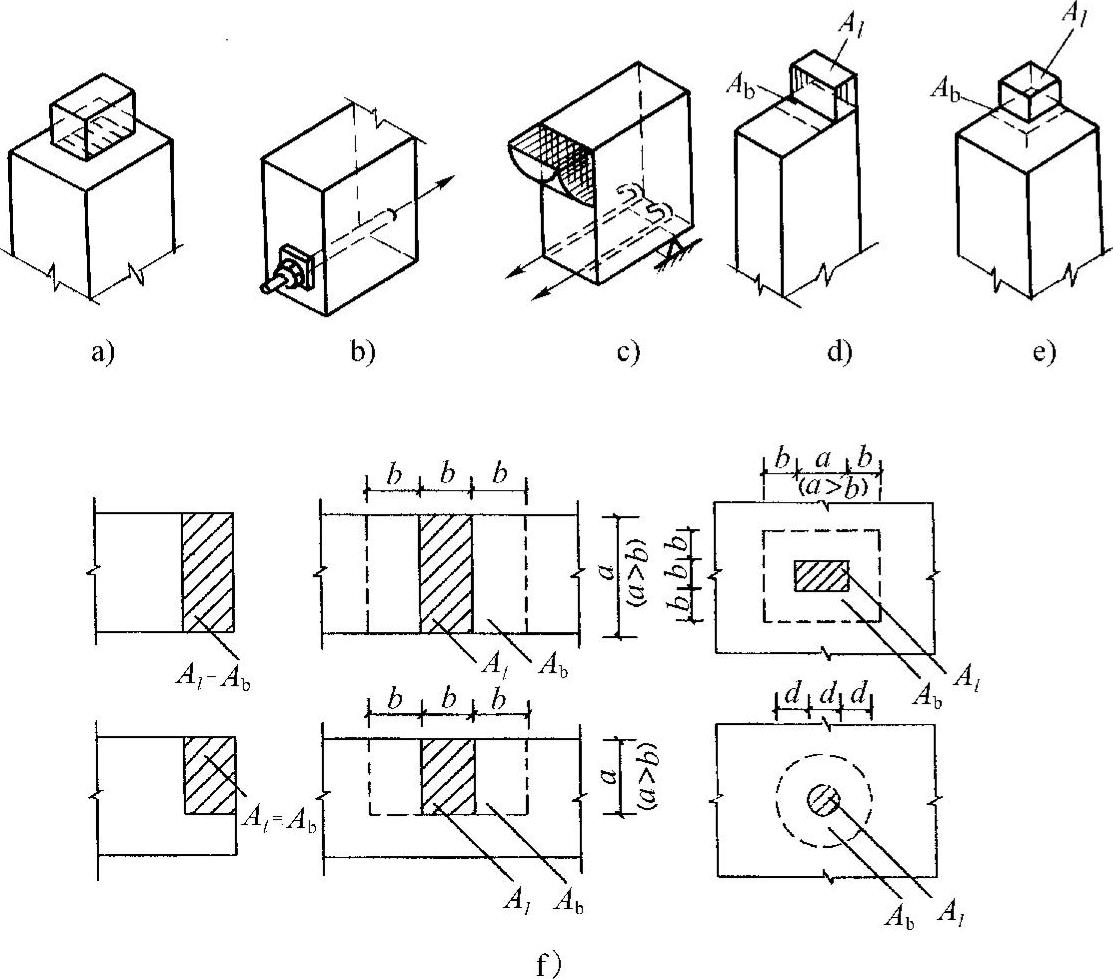
图2-7 局部承压
如上所述，横向变形约束条件对混凝土抗压强度影响很大。试验表明，要使混凝土抗压强度提高，可以在试件中配置横向钢箍或螺旋形箍筋以限制混凝土的横向变形，从而形成“约束混凝土”。
试验证明，加载速度快，测得的混凝土强度高，反之则低，因此，前面所述各强度是指在标准加荷速度的情况下测定的（每秒0.2～0.3N/mm2）。若加荷速度提高到每秒10N/mm2，强度可提高10%左右；在每秒105N/mm2快速加荷的冲击荷载作用下，强度可提高约60%；如加荷速度减慢，强度将降低。在极端情况下，加荷速度减少至零，即长期荷载作用下，混凝土棱柱体抗压强度将降低为0.8fc。
2.混凝土的抗拉强度
混凝土的抗拉强度ft是钢筋混凝土结构设计中计算抗裂度的重要指标。试验统计显示，ft仅为fcu的1/9～1/18左右；而且ft/fcu不是常数，它随fcu的增加而减小。凡影响抗压强度的因素，一般对抗拉强度也有相应的影响。然而，不同因素对抗压强度和抗拉强度的影响程度却不同。例如，水泥用量增加，可使抗压强度增加较多，而抗拉强度则增加较少。用碎石拌制的混凝土，其抗拉强度比用卵石的大，而骨料形状对抗压强度的影响则相对较小。
各国测定抗拉强度的方法不尽相同。我国近年来采用的直接受拉法，其试件是用钢模浇筑成型的100mm×100mm×500mm的棱柱体试件，两端设有埋深为150mm的对中等高肋钢筋（直径16～20mm）（图2-8a）。
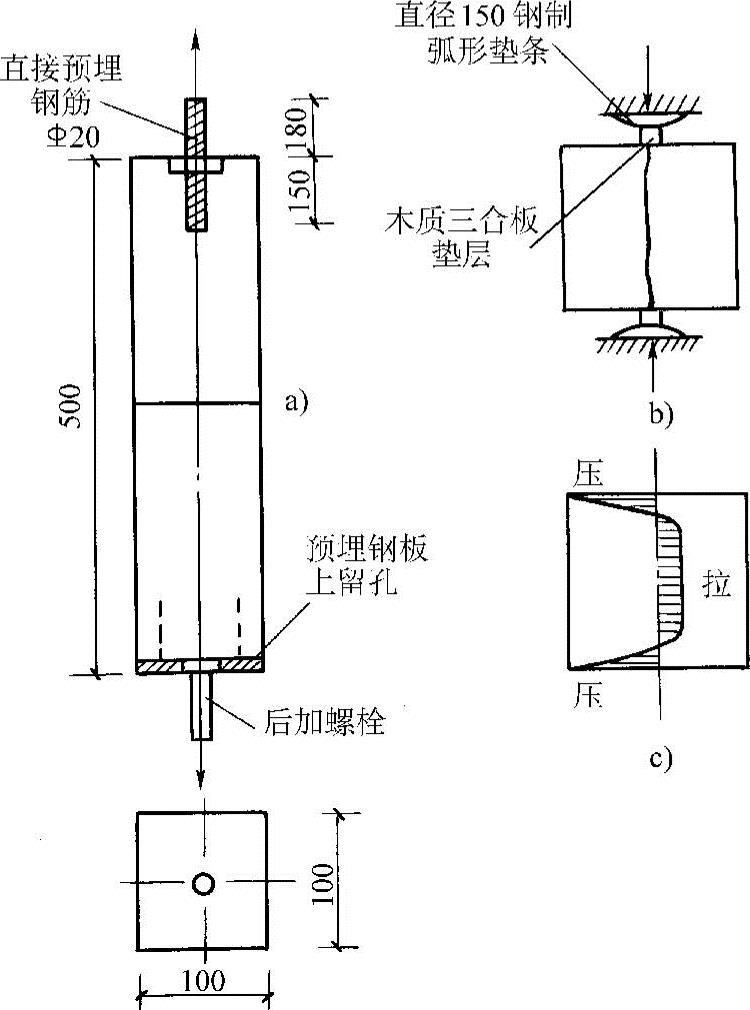
图2-8 测定混凝土抗拉强度的试验方法
试验机夹紧两端钢筋，使试件受拉，破坏时在试件中部产生断裂。这时测得的平均拉应力即为混凝土的轴心抗拉强度。但这种试验方法由于不易将拉力对中，会形成偏心影响。而且，因等高肋钢筋端部处的应力集中，会使断裂出现在埋入钢筋尽端的截面处。这些因素都对ft的正确量测有影响。
国内外也常用劈裂法测定混凝土的抗拉强度。它是将立方体试块（或平放的圆柱体试块）通过垫条施加线荷载p（图2-8b）。试块尺寸与测定立方体强度的试块大小相同，在通过中心的垂直截面上、下设一钢制弧形垫条及木质三合板垫层以使试块均匀受力。
试块垂直截面的应力分布如图2-8c，图中除上、下垫条附近为压应力外，中间绝大部分为均匀的拉应力。由于混凝土抗拉强度较抗压强度低很多，当拉应力达到混凝土的抗拉强度时，试块沿中间截面劈裂成两半。由弹性理论公式可求得劈拉强度fts为
式中 p——劈拉破坏时的荷载；
a——立方体试块的边长。
经实测统计得到100mm立方体的劈拉强度fts与150mm立方体的fcu近似关系为
fts=0.19f3/4cu （2-5）
由劈裂法测定的ft值，一般比直接受拉法测得的低，但也有相反的情况。这主要是由于试块与垫条接触处有应力集中，如果垫条太细，应力集中影响就很大，所测得的抗拉强度就比直接受拉法测得的低。过去常用5mm×5mm方钢垫条，所测得的抗拉强度一般均小于直接受拉法测得的强度。有的研究单位建议垫条改用18mm的扁铁。国际材料与结构研究协会（RILEM）建议垫条采用胶合板或硬纸板，宽15mm、厚4mm。当采用立方体试块时，垫条与试验机上下压板之间再安放有曲面的钢块，曲面直径为75mm。
我国试验给出轴心抗拉强度ft与立方体抗压强度fcu的关系为
根据与轴心受压强度相同的理由，考虑构件与试件的差别，规范[1]取用关系式
3.混凝土的疲劳强度
混凝土的疲劳强度由静载的混凝土强度乘以疲劳强度修正系数得到。原规范沿用原苏联的混凝土规范对混凝土的抗拉疲劳强度和抗压疲劳强度采用同一个疲劳强度修正系数，但国内外的试验研究说明，混凝土的抗压疲劳强度修正系数明显大于抗拉疲劳强度修正系数，所以本次修定采用大连理工大学的研究成果，分别给出了抗压和抗拉疲劳强度修正系数。
4.复合应力状态下的混凝土强度
上面所讲的抗压强度和抗拉强度均是指单轴向受力条件下所得到的混凝土强度。但实际上，结构物很少处于单向受压或单向受拉状态。工程上经常遇到的都是一些双向或三向受力的复合应力状态，例如前面所说的局部承压荷载下的混凝土以及双向板、壳、承受内压的油罐、原子能反应堆的压力容器等均属这些状态。所以研究复合应力状态下的混凝土强度条件，对进行合理设计是极为重要的。
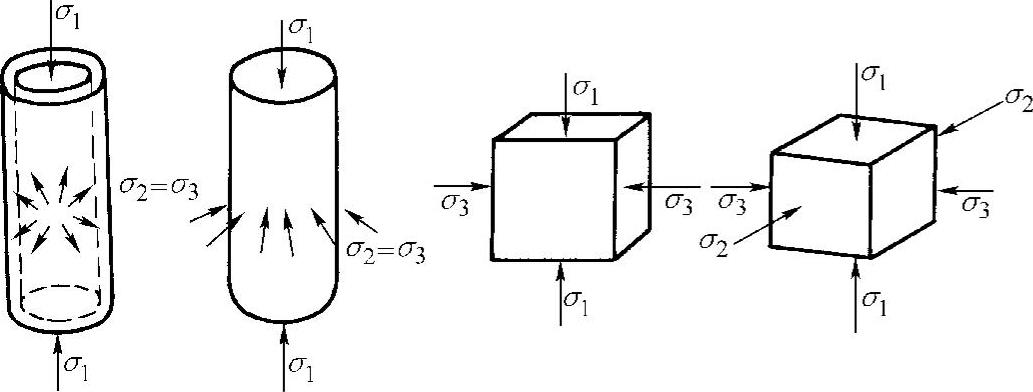
复合应力强度试验的试件形状大体可分为空心圆柱体、实心圆柱体、正方形板、立方体等几种。如图2-9所示，在空心圆柱体的两端施加纵向压力或拉力，并在其内部或外部施加液压，就可形成双向受压、双向受拉或一向受压一向受拉；如在两端施加一对扭转力矩，就可形成剪压或剪拉；实心圆柱体及立方体则可形成三向受力状态，但前者的侧向应力σ2=σ3，所以称为假三轴试验，而后者σ2可以不等于σ3，所以称为真三轴试验。正方形板则可形成两向受力状态。
根据现有的试验结果，可以得出双轴应力状态下混凝土强度的特点是：
（1）双向受压时，即两个方向的主应力为压应力，第三个方向的主应力为零时，混凝土的强度比单向受压的强度高。也就是说，一向抗压强度随另一向压应力的增加而增加，在双向等压应力的情况下，其强度比单向受压强度提高约16%。
(www.xing528.com)
图2-9 复合应力强度试验的试件形状及圆柱体受液压作用示意图
（2）双向受拉时，混凝土一向抗拉强度随另一向拉应力的增加而减小，但由于目前试验数据较少，所以近似认为混凝土一向抗拉强度基本上与另一向拉应力大小无关。也就是说，双向受拉时的混凝土强度与单向受拉强度基本一样。
（3）一向受拉一向受压时，混凝土抗压强度随另一向的拉应力的增加而降低。或者说，混凝土的抗拉强度随另一向的压应力的增加而降低，且混凝土的抗拉、抗压强度均低于单向受拉或单向受压的强度。设计时应引起注意。
由于复合应力状态下的试验方法很不统一，影响强度的因素很多，所得出的试验数据有时相差可达300%。根据各自的试验资料所提出的强度公式也多种多样。下面列举一些公式简略地反映这方面的研究情况。这些公式的形式及系数值，还值得进一步验证。
在实用上，对于双向受力情况，可以参考图2-10所示的典型破坏包络曲线。
图中分为三个区域：Ⅰ区为双向受压，Ⅱ区为双向受拉，Ⅲ区为一向受压、一向受拉。图中σ1、σ2为主应力，fc为单向受压时的极限强度。Kupfer和Gerstle给出了图2-10的破坏包络曲线的关系式为：
（1）双向受压
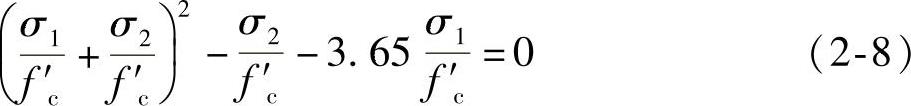
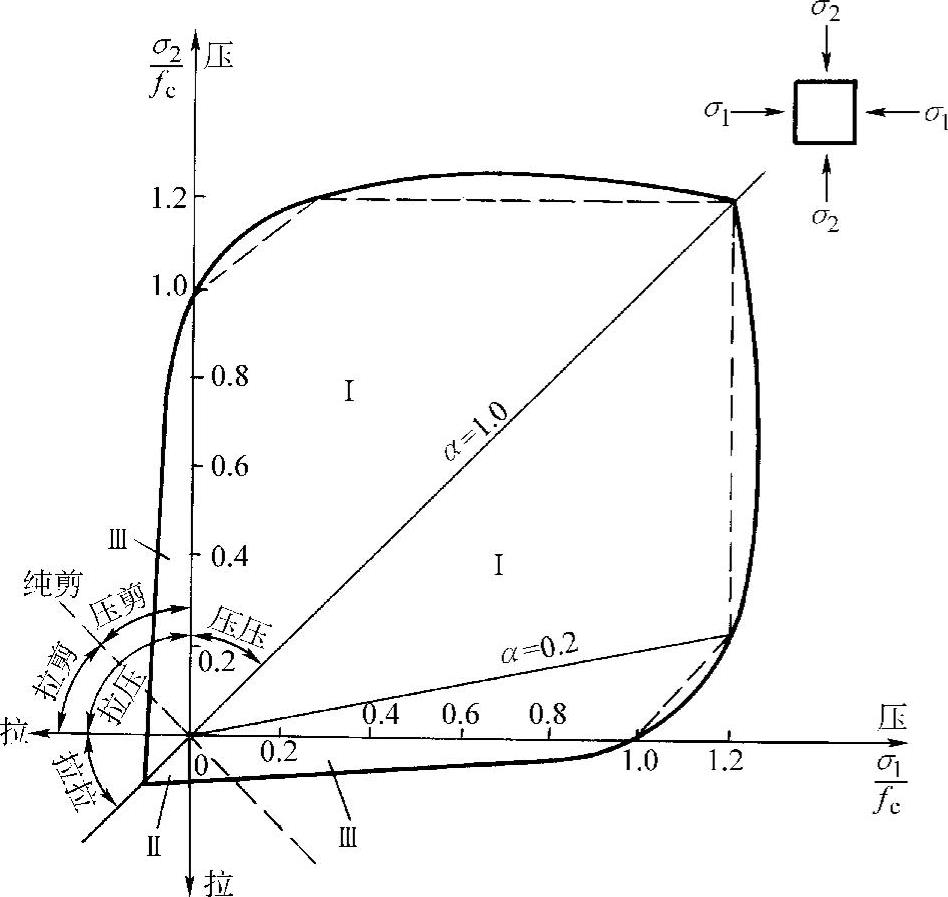
图2-10 混凝土双向应力下的强度曲线
或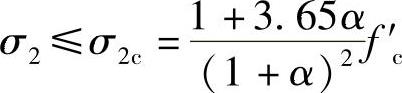 
σ1≤σ1c=ασ2c （2-9）
0≤α≤1
式中 α——两个方向主应力σ1与σ2的比值，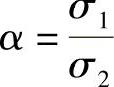
；
σ1c、σ2c——两个方向的最大压应力；
f′c——混凝土圆柱体的单轴抗压强度。对于σ1、σ2、f′c，当其为压应力时用负号。
（2）一向受拉，一向受压
当α≤-0.3048时， σ1≥ft （2-10）
当α>-0.3048时，
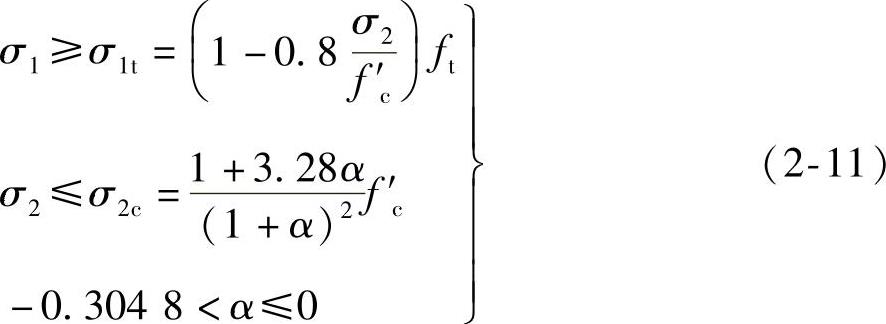
（3）双向受拉
式中 ft——混凝土的单轴抗拉强度。
在单轴向压应力σ及剪应力τ共同作用下，混凝土的破坏包络曲线可采用σ及τ为坐标来表示，如图2-11所示。图中曲线表示其抗剪强度随拉应力的增加而减小，随压应力的增加而增加，但当压应力大于（0.5～0.7）fc时，抗剪强度随压应力的增加而减小。同时，由于剪应力的存在，混凝土的抗压强度将低于单轴抗压强度。这一点在设计时应引起充分的注意。
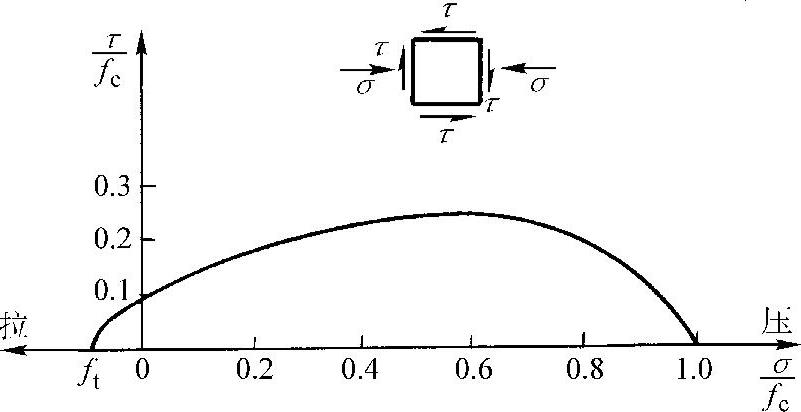
图2-11 混凝土的复合受力强度曲线
图2-11中的曲线可用下式表示：
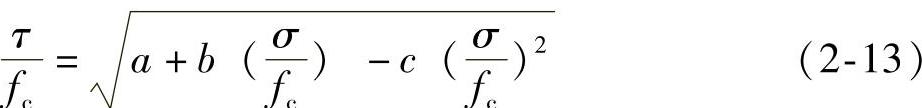
式中a、b、c为常数，可由试验求出。例如，有的剪压试验得出：a=0.00981、b=0.112、c=0.122。试验表明，加载次序、各向加载数值大小以及试件形状均会对试验结果有明显影响。
三向应力状态下，混凝土的强度特性与双轴应力状态类似，但三向受压状态混凝土强度的提高值比双向受压状态大得多，特别随侧向压应力的增加而很快增加，如图2-12所示。根据试验，大连理工大学得出混凝土在八面体应力空间破坏准则的数学表达式为：
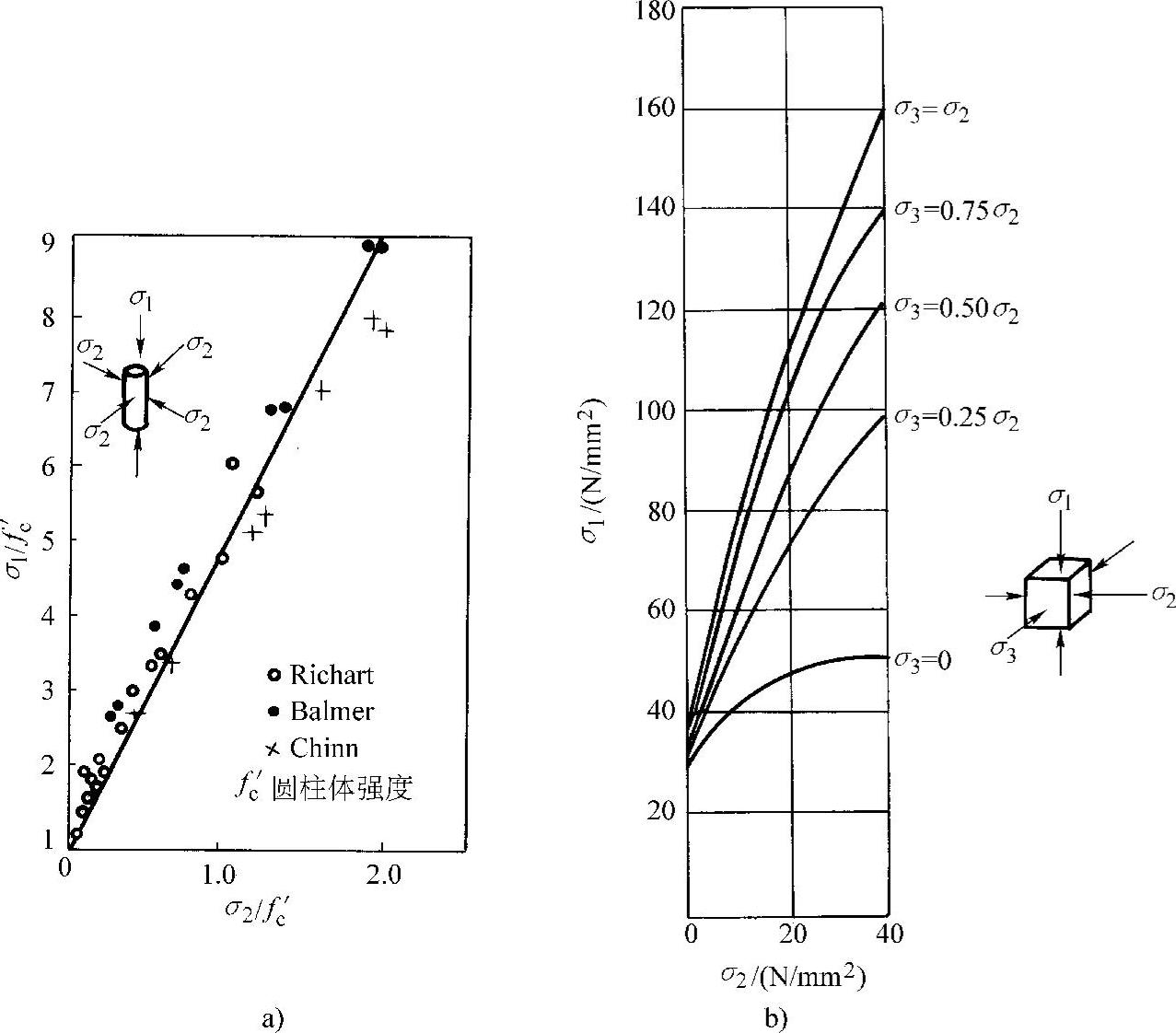
图2-12 混凝土三向受压的试验曲线
（1）拉子午线
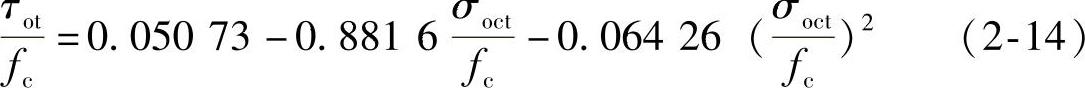
（2）压子午线
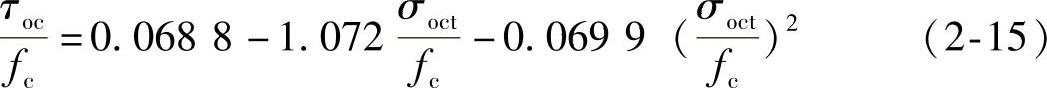
偏平面上罗德角0°≤θ≤60°的强度表达式如下：
τoct（θ）=τot-（τot-τoc）sin21.5θ （2-16）
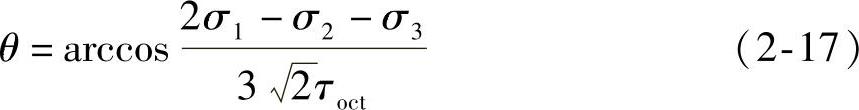
式中 τot，τoc——拉、压子午线上的八面体剪应力；
σoct——八面体正应力，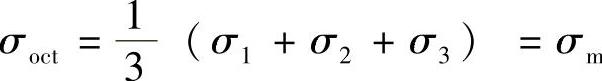
，σm为平均应力；
τoct——八面体剪应力，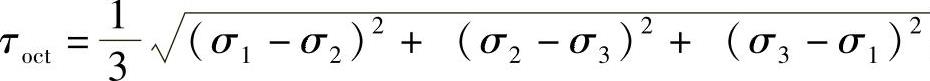
；
θ——相似角。
上述破坏准则与收集到的国内外试验结果的比较如图2-13及图2-14所示。由以上两图可见，上述破坏准则与试验值符合较好。
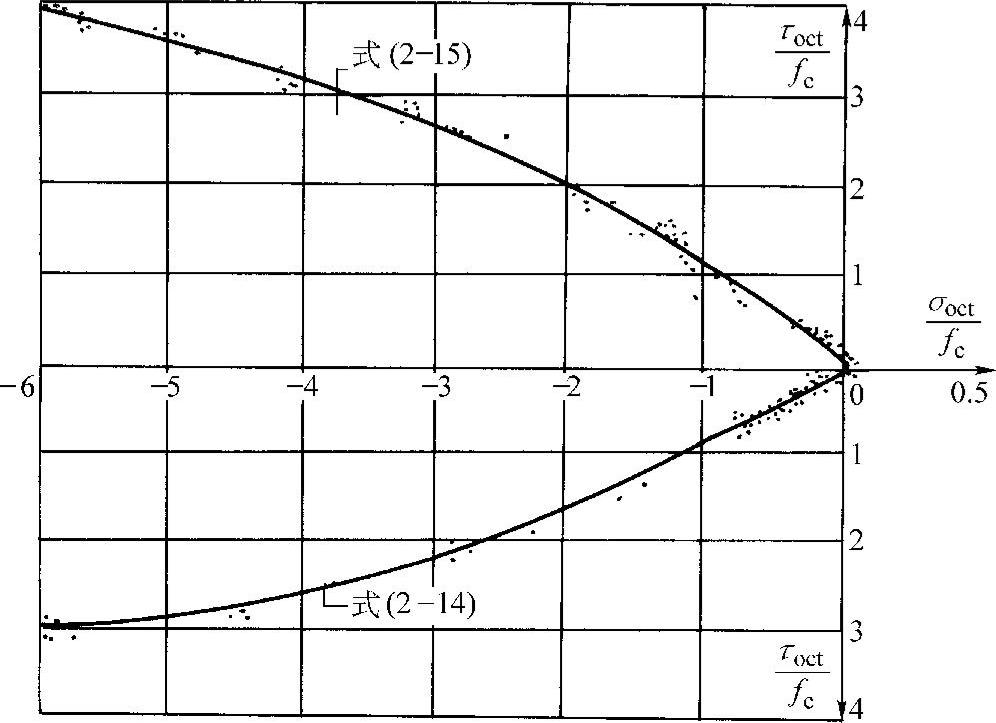
图2-13 拉压子午线计算值与试验值的比较
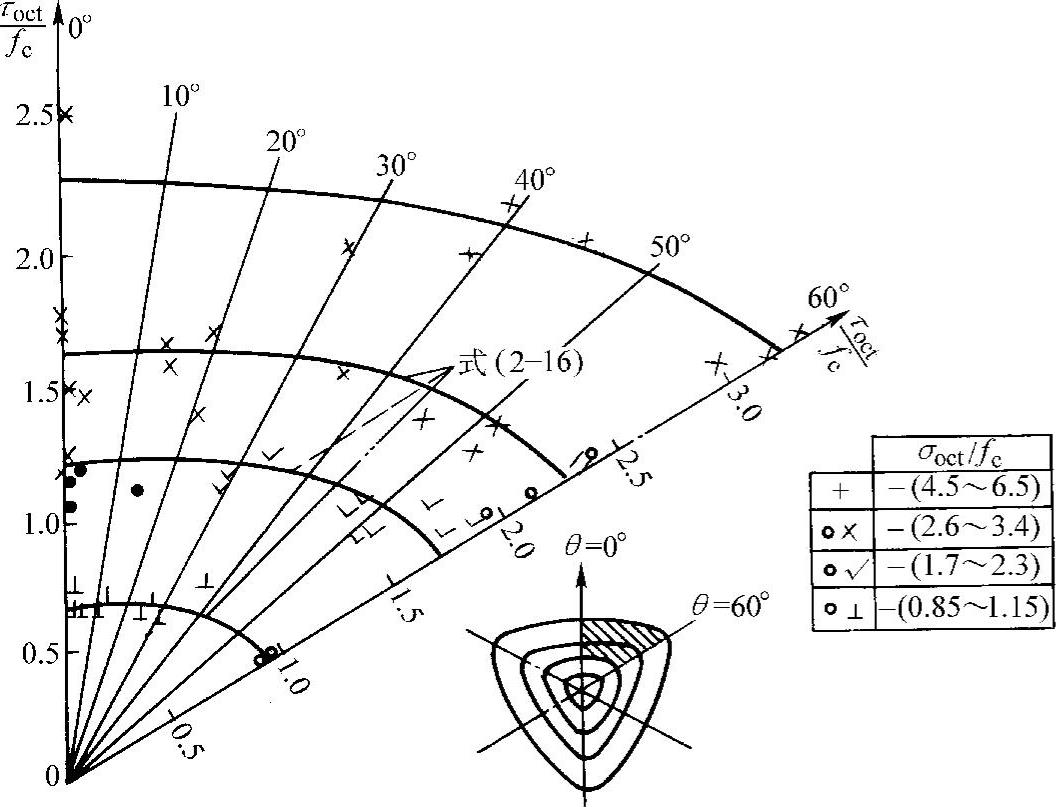
图2-14 偏平面上强度包络线计算值与试验值比较
混凝土设计规范对混凝土二轴强度包络线给出下列方程对于拉-拉应力状态：f21+f22-2vf1f2=（ft，r）2 （2-18）
对于压-压应力状态：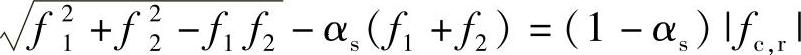
(2-19)
对于拉-压应力状态：（竖向）
对于拉-压应力状态：（水平向）
式中 fr——混凝土多轴强度代表值，受拉为负，受压为正，且f1≥f2；
fc，r、ft，r——混凝土单轴抗压和单轴抗拉强度特征值；
αs——受剪屈服参数；
r——双轴受压强度提高系数，r=1.15～1.30，可根据试验确定，一般可取1.2。
二轴、三轴强度也可查表获得，见《混凝土结构设计规范》GB50010—2010。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
