发动机原理：单质量系统自由振动

图9.3所示为分析车身振动的单质量系统模型，它由车身质量m2和弹簧刚度K、减振器阻尼系数为C的悬架组成。q是输入的路面不平度函数。

图9.3　车身振动的单质量系统模型

车身垂直位移坐标z的原点取在静力平衡位置，根据牛顿第二定律，得到描述系统运动的微分方程为：

此方程的解由自由振动齐次方程的解与非齐次方程特解之和组成。

令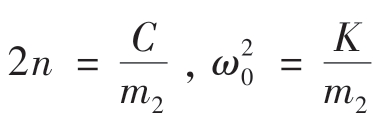，则齐次方程为：

ω0称为系统固有圆频率，而阻尼对运动的影响取决于n和ω0的比值ζ，ζ称为阻尼比，即

汽车悬架系统阻尼比ζ的数值通常在0.25左右，属于小阻尼，此时微分方程的解为：

这个解说明，有阻尼自由振动时，质量m2以有阻尼固有频率振动，其振幅按e-nt衰减，如图9.4所示。

图9.4　衰减振动曲线(www.xing528.com)

阻尼比ζ对衰减振动有以下两方面的影响。

（1）与有阻尼固有频率ωr有关。

由式（9-10）可知，ζ增大，ωr下降，当ζ=1时，ωr=0，此时运动失去振荡特征。汽车悬挂系统阻尼比ζ大约为0.25，ωr比ω0只下降了3％左右，在工程上可以近似认为ωr≈ω0，车身部分振动的固有圆频率ω0（rad/s）、固有频率f0（s-1或Hz）为：

（2）决定振幅的衰减程度。

图9.4上两个相邻的振幅A1与A2之比称为减幅系数，用d表示为

对式（9-12）取自然对数：

可以由实测的衰减振动曲线得到减幅系数d，由下式求出阻尼比ζ：