四轮汽车振动系统简化解析

图9.1所示为一个把汽车车身质量看作刚体的立体模型。汽车的悬挂（车身）质量为m2，它由车身、车架及其上的总成构成。该质量绕通过质心的横轴y的转动惯量为Iy，悬挂质量通过减振器和悬架弹簧与车轴、车轮相连接。车轮、车轴构成的非悬挂（车轮）质量为m1。车轮再经过具有一定弹性和阻尼的轮胎支撑在不平的路面上。车身质量在讨论平顺性时主要考虑垂直、俯仰、侧倾3个自由度，4个车轮质量有4个自由度，这一立体模型共7个自由度。

图9.1　四轮汽车简化的立体模型

当汽车对称于其纵轴线，且左、右车辙的不平度函数x（I）=y（I）时，汽车车身只有垂直振动z和俯仰振动φ，这两个自由度的振动对平顺性影响最大。图9.1所示为汽车简化成4个自由度的平面模型。在这个模型中，又因轮胎阻尼较小而予以忽略，同时把质量为m2，转动惯量为Iy的车身按动力学等效的条件分解为前轴上、后轴上及质心c上的三个集中质量m2f、m2r、m2c。这三个质量由无质量的刚性杆连接，它们的大小由下述三个条件决定。

（1）总质量保持不变，即：

（2）质心位置不变，即：

（3）转动惯量Iy的值保持不变，即：

式中　ρy——绕横轴y的回转半径；(www.xing528.com)

a、b——车身质量部分的质心至前、后轴的距离。

由上述三式得出三个集中质量的值为：

式中　L——轴距。

通常令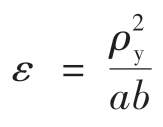，称其为悬挂质量分配系数。由式（9-6）可知，当ε=1时，联系质量m2c=0。据统计，大部分汽车ε=0.8～1.2，即接近1。而通过分析可知，在ε=1的情况下，前、后轴上方车身部分集中质量m2f、m2r的垂直方向运动是相互独立的。这样在ε=1的情况下，当前轮遇到由路面不平度而引起的振动时，质量m2f运动而质量m2r不运动，反之亦然。因此在这种特殊情况下，可以分别讨论图9.2上m2f和前轮轴以及m2r和后轮轴所构成的两个双质量系统的振动。

图9.2　双轴汽车简化的平面模型

在远离车轮部分固有频率ft（10～16 Hz）的较低激振频率范围内（如5 Hz以下），轮胎动变形很小，忽略其弹性与车轮质量，得到分析车身垂直振动最简单的单质量系统。