汽车理论：线性二自由度汽车模型的运动微分方程

为了便于掌握操纵稳定性的基本特性，我们将对一简化为线性二自由度的汽车模型进行研究。在分析中忽略转向系统的影响，直接以前轮转角作为输入；忽略悬架的作用，认为汽车车厢只做平行于地面的平面运动，即汽车沿z轴的位移、绕y轴的俯仰角与绕x轴的侧倾角均为零。另外，在本节的特定条件下，将汽车沿x轴的前进速度u视为不变。因此，汽车只有沿y轴的侧向运动与绕z轴的横摆运动这两个自由度。此外，汽车的侧向加速度限定在0.4g以下，轮胎侧偏特性处于线性范围内。在建立运动微分方程时还假设：驱动力不大，不考虑地面切向力对轮胎侧偏特性的影响，没有空气动力的作用，忽略左、右车轮轮胎由于载荷的变化而引起的轮胎特性变化以及轮胎回正力矩的作用。这样，实际汽车便简化成一个两轮摩托车模型，如图8.18所示。它是一个由前、后两个有侧向弹性的轮胎支承于地面、具有侧向及横摆运动的二自由度汽车模型。

图8.18　二自由度汽车模型

在分析时，我们令车辆坐标系的原点与汽车质心重合。

显然，汽车的质量分布参数，如转动惯量等，对固结于汽车的这一动坐标系而言为常数，这正是采用车辆坐标系的方便之处。因此，只要将汽车的（绝对）加速度与（绝对）角加速度及外力与外力矩沿车辆坐标系的轴线分解，就可以列出沿这些坐标轴的运动微分方程。

下面依次确定：汽车质心的（绝对）加速度在车辆坐标系上的分量，二自由度汽车受到的外力与绕质心的外力矩，外力、外力矩与汽车运动参数的关系。最后，列出二自由度汽车的运动微分方程式。

首先确定汽车质心的（绝对）加速度在车辆坐标系上的分量。

如图8.19所示，Ox与Oy为车辆坐标系的纵轴与横轴。质心速度v1于t时刻在Ox轴上的分量为u，在Oy轴上的分量为v。由于汽车在转向行驶时伴有平移和转动，在t+Δt时刻，车辆坐标系中质心速度的大小与方向均发生变化，而且车辆坐标系的纵轴与横轴的方向亦发生变化。所以，沿Ox轴速度分量的变化为：

图8.19　利用固结于汽车的车辆坐标系分析汽车的运动

(u+Δu)cosΔθ-u-(v+Δv)sinΔθ=ucosΔθ+ΔucosΔθ-u-vsinΔθ-ΔvsinΔθ

考虑到Δθ很小并忽略二阶微量，上式变为Δu-vΔθ除以Δt并取极限，便是汽车质心绝对加速度在车辆坐标系x轴上的分量，即：

同理，汽车质心绝对加速度沿横轴Oy上的分量为：

由图8.18可知，二自由度汽车受到的外力沿y轴方向的合力与绕质心的力矩和为：(www.xing528.com)

式中　FY1、FY2——地面对前、后轮的侧向反作用力，即侧偏力；

δ——前轮转角。

考虑到δ角较小，FY1、FY2为侧偏力，则式（8-4）可被改写作：

汽车前、后轮侧偏角与其运动参数有关。如图8.18所示，汽车前、后轴中点的速度为u1、u2，侧偏角为α1、α2，质心的侧偏角为β，β=v/u。ζ是u1与x轴的夹角，其值为：

根据坐标系的规定，前、后轮侧偏角为：

由此，可列出外力、外力矩与汽车运动参数的关系式为：

所以，二自由度汽车的运动微分方程式为：

式中IZ——汽车绕z轴的转动惯量（kg·m2）；

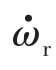——汽车横摆角加速度（rad/s2）。

整理后得二自由度汽车运动微分方程式为：

这个联立方程式虽很简单，但包含了最重要的汽车质量与轮胎侧偏刚度两方面的参数，所以能够反映汽车曲线运动最基本的特征。